位运算核心技巧解析：实用优化与C语言源码示例

在编程中，直接操作整数的二进制位，是一种强大且高效的底层技术。它不仅是编写高性能代码、进行状态压缩或内存优化的利器，更能让你以更简洁优雅的方式解决特定问题。今天，我们就来系统地梳理一下位运算的常见操作与实用技巧，并附上可直接运行的C语言代码示例。

位运算的优势

为什么我们要关注位运算？

• 速度极快：作为最底层的运算之一，它比普通算术运算快得多。
• 内存高效：执行效率高，且占用内存极少。
• 特性独特：直接操作二进制数，能利用二进制的特性解决一些特殊问题。
• 代码简洁：恰当的位运算能让程序逻辑更清晰、代码更紧凑。
• 状态表示：可以方便地使用一个整数来表示和操作一组状态标志。

基本运算符与优先级

以下是C语言中基本的位运算符（假设a和b为整数）：

含义	C语言运算符
按位与	a & b
按位或	a \| b
按位异或	a ^ b
按位取反	~a
左移	a << b
带符号右移	a >> b

这些运算符的优先级从高到低排列如下（为避免混淆，实际编码中建议多用括号）：

1. ~ (取反)
2. <<、>> (移位)
3. & (与)
4. ^ (异或)
5. \| (或)
6. &=, ^=, |=, <<=, >>= (复合赋值)

常用位变换操作概览

在深入每个操作前，我们先通过一张表格快速了解一些常见的二进制位变换目标及其对应的运算思路，这对于理解后续的计算机基础概念很有帮助。

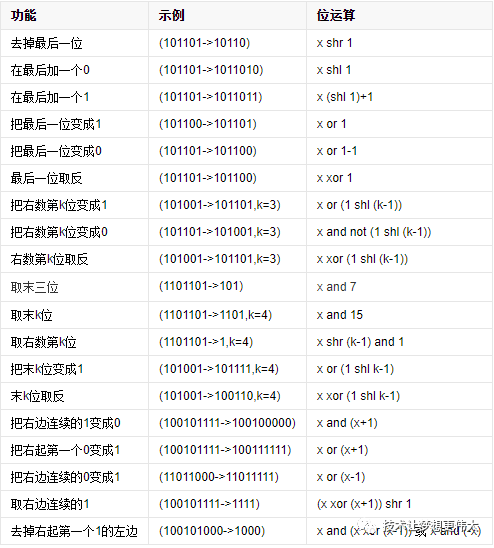
按位与 (&) 操作技巧

1. 判断奇偶数
利用二进制数最低位的特性：奇数为1，偶数为0。

if (x & 1) {
    // x 是奇数
}

2. 判断某二进制位是否为1
例如，检查一个数 n 的第7位（从右向左，从0开始计数）是否为1。0x40 的二进制是 0100 0000。

if (n & 0x40) {
    // 第7位是1
}

3. 按字节读取数据
从一个32位整数中依次提取出它的四个字节。

(x >>  0) & 0x000000ff;  /* 获取最低字节（第0字节） */
(x >>  8) & 0x000000ff;  /* 获取第1字节 */
(x >> 16) & 0x000000ff;  /* 获取第2字节 */
(x >> 24) & 0x000000ff;  /* 获取第3字节（最高字节） */

4. 判断一个数是否为2的幂
一个数是2的幂，当且仅当其二进制表示中只有一个1。n & (n-1) 可以去掉最右边的1。

bool isPowerOfTwo(int n) {
    if (n <= 0) return false;
    return (n & (n - 1)) == 0;
}

5. 对2的n次方取余
这个方法比 % 运算符更快。

int getRemainder(int num, int n) { // 除数 = 2^n
    int i = 1 << n; // 计算 2^n
    return num & (i - 1); // 等价于 num % (2^n)
}

6. 统计二进制中1的个数（Brian Kernighan算法）
x = x & (x-1) 每次会消去x二进制表示中最右边的1。

int countBits(int x) {
    int count = 0;
    while (x) {
        count++;
        x = x & (x - 1);
    }
    return count;
}

按位或 (|) 操作技巧

1. 状态压缩与组合编码
将多个布尔状态或标志位合并存储在一个整数的不同位上，节省空间。

#define FLAG_A (1 << 0)
#define FLAG_B (1 << 1)
#define FLAG_C (1 << 2)

int state = 0;
state |= FLAG_A; // 打开A状态
state |= FLAG_C; // 打开C状态

if (state & FLAG_B) {
    // 检查B状态是否开启
}

2. 求二进制表达中0的个数（从低位开始连续计数）
下面的方法用于计算从最低位开始，直到遇到第一个1之前，共有多少个0。

int countTrailingZeros(int x) {
    int count = 0;
    while ((x | (x + 1)) == x) { // 等价于检查 x+1 是否没有引入新1？
        count++;
        x |= (x + 1); // 将最低位的0变为1
    }
    return count;
}

按位异或 (^) 操作技巧

1. 交换两个整数（无需临时变量）
利用 a ^ b ^ b = a 的性质。

void swap(int *a, int *b) {
    *a ^= *b;
    *b ^= *a;
    *a ^= *b;
}

2. 判断两个数是否异号
两个数异号，则它们的最高位（符号位）不同，异或结果的符号位为1（负数）。

int x = -1, y = 2;
bool isOpposite = ((x ^ y) < 0); // true

int a = 3, b = 2;
bool isOpposite2 = ((a ^ b) < 0); // false

3. 简单数据加密与解密
使用一个密钥对数据进行异或加密，再次用相同密钥异或即可解密。

#include <stdio.h>
#include <string.h>
#define KEY 0x86

int main() {
    char plain_text[16] = {"Hello World!"};
    char encrypted[16] = {0}, decrypted[16] = {0};

    // 加密
    for(int i = 0; i < strlen(plain_text); i++) {
        encrypted[i] = plain_text[i] ^ KEY;
    }
    // 解密
    for(int i = 0; i < strlen(encrypted); i++) {
        decrypted[i] = encrypted[i] ^ KEY;
    }

    printf("原文:  %s\n", plain_text);
    printf("密文:  %s\n", encrypted);
    printf("解密后: %s\n", decrypted);
    return 0;
}

4. 找出数组中唯一不重复的数字
如果一个数组中，除了某个数字只出现一次，其他都出现了两次，那么将所有数字异或起来，结果就是那个只出现一次的数。

int findUnique(int arr[], int len) {
    int result = arr[0];
    for(int i = 1; i < len; i++) {
        result ^= arr[i];
    }
    return result;
}

按位取反 (~) 与移位组合技巧

1. 改变符号（取相反数）
利用补码表示法。

int reverseSign(int a) {
    return ~a + 1; // 等价于 -a
}

2. 高效取绝对值
无需分支判断，性能更好。理解它需要对计算机基础中的补码有清晰认识。

int abs_no_branch(int n) {
    int sign = n >> 31; // 符号扩展，正数为0，负数为-1 (0xFFFFFFFF)
    return (n ^ sign) - sign;
}

3. 将指定位置1或置0

• 将数 n 的第 m 位（从低位开始，1-based）置1：

  int setBit(int n, int m) {
  return n | (1 << (m - 1));
  }

• 将数 n 的第 m 位置0：

  int clearBit(int n, int m) {
  return n & ~(1 << (m - 1));
  }

移位 (<<, >>) 操作技巧

1. 快速计算2的n次方

int powerOfTwo = 1 << n; // 计算 2^n

2. 高低位交换（以16位为例）

unsigned short a = 34520;
a = (a >> 8) | (a << 8); // 交换高8位和低8位

3. 二进制逆序（以16位为例，分治法）

unsigned short a = 34520;
// 逆序过程：1位交换 -> 2位交换 -> 4位交换 -> 8位交换
a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1);
a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2);
a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4);
a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8);

4. 求不大于N的最大2的幂
这个方法通过将最高位1后面的所有位都填充为1，再加1右移得到。

int floorPowerOfTwo(int n) {
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16; // 对于32位整数
    return (n + 1) >> 1;
}

5. 快速幂算法（计算 m^n）
利用指数的二进制分解。

int fastPow(int m, int n) {
    int result = 1;
    while (n > 0) {
        if (n & 1) { // 如果当前二进制位为1
            result *= m;
        }
        m *= m;      // m 自乘
        n >>= 1;     // n 右移一位
    }
    return result;
}

位图操作宏定义

位图是算法/数据结构中常用技巧，用于高效表示和操作一组布尔值。

// 将 x 的第 n 位清零 (0-based)
#define CLEAR_BIT(x, n)   ((x) &= ~(1ULL << (n)))
// 将 x 的第 n 位置一
#define SET_BIT(x, n)     ((x) |= (1ULL << (n)))
// 获取 x 的第 n 位的值 (0 或 1)
#define GET_BIT(x, n)     (((x) >> (n)) & 1)
// 切换 x 的第 n 位的值 (0变1，1变0)
#define TOGGLE_BIT(x, n)  ((x) ^= (1ULL << (n)))

更广阔的位运算世界

位运算的技巧远不止于此，在图形学、密码学、系统编程和算法竞赛等领域有更深入和精妙的应用，例如：

• 并行位计数（Population Count）
• 查找前导零（Leading Zero Count）
• 位反转更高效的算法
• 交织位（Morton Code计算）
• 利用位运算进行边界检查与数值比较
• 各种无需分支的条件操作

如果想深入探索这个充满技巧的领域，可以参考斯坦福大学的“Bit Twiddling Hacks”资源库（graphics.stanford.edu/~seander/bithacks.html），那里收集了大量极致的位运算技巧。

掌握位运算，犹如获得了一把打开底层性能优化和优雅编码之门的钥匙。希望本文整理的这些核心技巧和源码能为你带来启发。如果你对这些底层技术感兴趣，欢迎在云栈社区与其他开发者继续交流探讨。