现在让我为您奔走,我会努力做到不可能之事。
——威廉·莎士比亚,《凯撒大帝》,里加律斯对布鲁塔斯所说
韦氏词典对“不可能”的定义是“无法存在或出现”,但我们并不总是这么用这个词。我们经常用“不可能”(impossible)来代替“不大可能”(improbable)。我们用它来描述有些尽管并非完全不可能,但还是很难做到的事。
如果我们把一个打乱了的魔方给一个新手,他没办法把它复原,因为背后的逻辑要求太复杂了,在没有人帮助的情况下,魔方很难复原。乱拧一气复原魔方的概率更是低之又低。这时,我们就会说他不可能复原魔方。同样,对于一个没什么经验的保龄球选手来说,他几乎不可能打出300分的完美比赛。一只猴子也几乎不可能用键盘敲出莎士比亚全集。
这种“大海捞针”式的情景并非真的不可能,而是因为概率太低,就好像真的不可能一样。(我们需要指出,某些此类场景对于任何个人来说都是没有希望的,却很可能在某个人身上发生,比如中彩票。)
有些事在实际上不可能,例如用手写出 π 的前 10^{10^{10}} 位数字。有很多因素限制了我们这样做:人类的寿命没有长到能写出这么多数字,而且我们还不知道 π 的这么多位数字。即便我们知道,宇宙中也没有足够的墨水和纸让我们把它写出来。这是不可能的。
有些事被认为在物理上不可能。如果某些想法或者行动是可能的,那么它们就会违背我们对世界的认知。它们有悖于我们相信的物理定律。永动机就是个最好的例子。存在一个无须外部能量就能永远工作的机器听起来过于荒唐,它违背了包括能量守恒定律在内的多个物理定律。
当然,在很长一段时间里,我们对于物理或者生物领域的认知都是错误的。在4分钟内跑完1英里曾被认为是不可能的,但是罗杰·班尼斯特在1954年颠覆了我们的认知。载人飞行曾经也被认为是天方夜谭,但是莱特兄弟证明了这并非幻想。
当化学家们发现铅和金是两种不同的元素时,能点石成金的贤者之石或炼金术也就成了无稽之谈。但是,粒子加速器的诞生,让炼金术士们的梦想也变得可能,尽管并不实际。
时至今日,因为无法在现有科学框架中实现,有些事情还被认为不可能。在18世纪后半叶,学者们认为石头不可能从天而降;他们认为除了月亮,不存在其他的小型天体。他们把陨石(“雷电石”)的目击报告当作民间传说。在1768年,包括年轻的拉瓦锡在内的一个三人团队用现代化学手段研究了一块陨石。他们的结论是,它是一束闪电击中富含黄铁矿的砂石的产物。
1807年,美国耶鲁大学的两位教授发表了一篇论文,论述了一块落在康涅狄格州韦斯顿镇的陨石。出于怀疑,(受过科学教育的)时任总统托马斯·杰斐逊声称:“他们可能是正确的,但对于我来说,比起石头从天而降,还是两位洋基教授撒谎更有可能。”这则逸闻广为流传,不过未必真实,至少存在添油加醋的可能。不过它的确反映了当时人们的看法。
有些事情被认为不可能,则是因为人们不够创新或是过于短视,想象不到它们如何成真。如果我们向19世纪的人描述现代的计算机技术,他们一定会说,这样的机器是不可能存在的。在20世纪50年代时,简单(以今天的标准来看)的计算机也要占据整个房间。如果我们对50年代的人说,现如今我们把更强大的计算机放在口袋中或者手腕上,他们肯定会怀疑地摇头,说这不可能。
01 数学上不可能
某事在数学上不可能是指什么呢?我们又如何证明它不可能呢?
让我们来看看不可能性定理的一个简单例子。这个例子是有关偶数的,比如 0、8、- 102 等。我们都知道偶数是什么,但为了在数学中运用偶数,我们必须清楚明白地定义它们:如果存在整数 k,使得 n=2k,则 n 是偶数。因为 0 = 2·0,8 = 2·4,-102 = 2(-51),所以它们都是偶数。
我们可以用这个定义和整数的性质来证明一个我们都知道的定理:两个偶数的和不可能为奇数。证明如下:设 m和n是偶数,则存在整数j和k,使得m=2j,n=2k。那么m+n=2j+2k=2(j+k)。因为整数的和还是整数,所以j+k是整数。因此m+n是偶数。一个整数不可能既是偶数又是奇数,所以我们的不可能性定理得证。
我们从这个例子中能学到几件事。正如存在无穷多偶数一样,用尺规可以作无穷多的图形。我们不必检查所有可能的和来证明上述定理,只需要整数和偶数的一般性质来证明它。同样,可以用直线和圆的一般性质来证明我们的不可能性定理。
此外,如果我们只有偶数,那么它们的和也总是偶数。无论用什么顺序,加了多少个偶数,我们永远也不会“离开”偶数的集合并得到一个奇数。我们的和不会是 257 或者 1301,这不可能。我们将会看到,这和第 1 章提到的可作图数的集合类似;如果对可作图数进行特定的算术运算,我们只会得到其他可作图数。
偶数相加的例子可能看起来太简单了(尽管并非如此),并且可能有点儿牵强。因此,我们现在要来看一个更有趣一点儿的不可能性的例子。这次,我们的证明还是关于奇数和偶数的集合的。
02 萨姆·劳埃德的无解之谜
1880 年,就像一个世纪之后的魔方那样,一个机械智力游戏风靡美国。这个机械游戏就是 15 - 数字推盘游戏。时至今日,我们仍能找到它的身影。游戏的目标是通过在一个 4×4 的板中上下左右滑动 15 个有编号的方块,来让它们按编号顺序排列好。
那个时候,著名的美国智力游戏设计师萨姆·劳埃德悬赏 1000 美元(约合现在的 25 000 美元)求解他的 15 - 数字推盘游戏。劳埃德的游戏和一般游戏相差无几,但它的初始方块配置很特别:方块按数字顺序排列,但是 14 和 15 是反过来的(图 2.1)。

图 2.1 萨姆·劳埃德的 15- 数字推盘游戏(图文:谜题大陆的 14-15 谜题)(S. Loyd, 1914,《萨姆·劳埃德的智力游戏百科》,纽约:Lamb 出版社)
劳埃德可不是乱花钱的人。他知道自己永远不用付钱,因为在 1879 年,两名数学家证明了这样的初始配置是不可解的。让我们来看看为什么。
要解决 15 - 数字推盘游戏,我们必须把编号按从左到右、从上到下的顺序用线连起来。从结果来说,为了让证明更简单,我们需要改变胜利条件:方块的编号需要按蛇形排列——第一行从左到右,第二行从右到左,第三行从左到右,第四行从右到左。不过我们不会改变游戏规则。相对地,可以想象成我们把新的编号贴到了方块上——把 8 贴到 5 上,把 7 贴到 6 上,以此类推(图 2.2)。
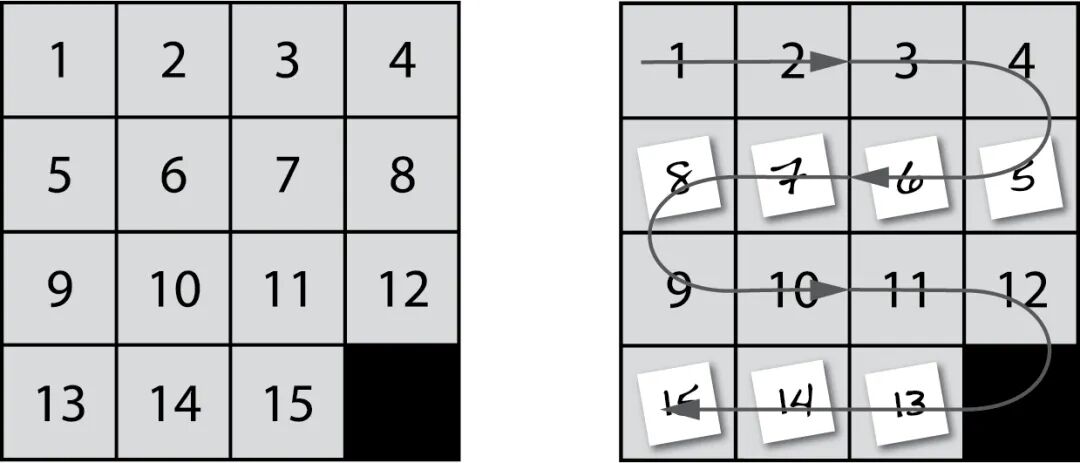
图 2.2 重新编号的 15- 数字推盘游戏
假设我们拿到了一个打乱顺序的 15 - 数字推盘游戏,如图 2.3 所示。我们把编号拿出来,然后按蛇形顺序列出,并且跳过空格。在这个例子中,这个列表是 2、13、5、1、4、12、11、10、3、14、15、6、9、7、8。对于表中的每个数字,我们都记录它右边的数中有多少个比它小。2 的右边只有 1 个比它小的数,13 的右边有 11 个数比它小,以此类推。然后我们把这些数加起来,得到的和是 44。也就是说,一共有 44 对方块按错误的顺序排列了,这也被叫作逆序对。最终的答案中应该没有逆序对。表 2.1 列出了我们的例子中的逆序对。

图 2.3 一个打乱顺序的 15- 数字推盘游戏
表 2.1 我们的 15- 数字推盘游戏中的逆序对

现在我们把一个方块推入空格,然后看看逆序对有什么变化。如果把一个方块向左或者向右推入空格,比如例子中的 14 或者 15,那么序列没有改变,因此逆序对的数量也不变。如果我们在蛇形排列换行的地方把一个方块上移或者下移,序列也不会改变。
如果我们在其他地方上移或者下移方块,逆序对的数量就会改变了。但是这不会影响所有的方块,这样的一步只会影响到 3 个、5 个或者 7 个方块。这取决于空格的位置,以及究竟是哪个方块被推进了空格。只有这几个方块的逆序对会被影响。
如果我们下移 12,它就被挪到了 14 和 15 之间。所以它只会影响 12、11、10、3 和 14。注意,12 比 11、10 还有 3 都大,但是小于 14。所以,当它被移走之后,它的逆序对数量减少了 3,但 14 的逆序对数量增加了 1。
这样,总逆序对数量就减少了 2,变成了 42。同样,如果我们把 9 上移,序列会从 15、6、9 变成 9、15、6。因为 9 比 6 大,比 15 小,它的逆序对数量会增加 1,15 的逆序对数量会减少 1。因此,总的逆序对数量保持不变,如表 2.2 所示。
表 2.2 移动方块 12 和方块 9 之后的逆序对情况
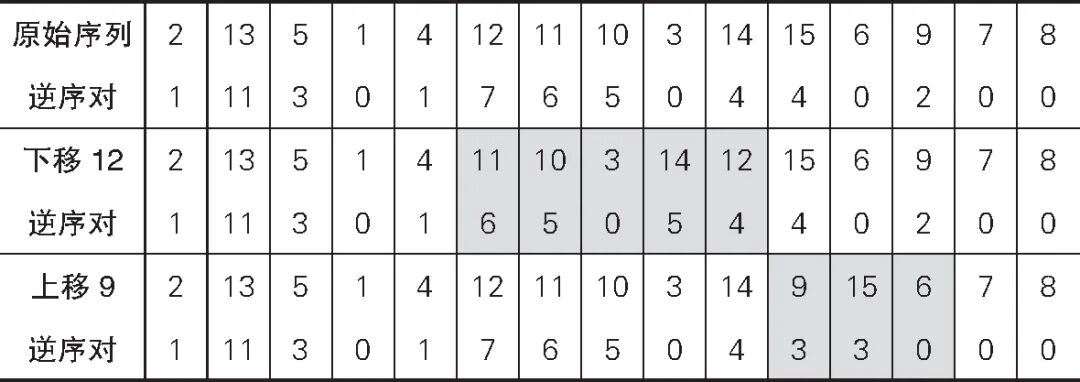
通常,垂直移动会影响 k+1个方块,其中k可能是 2、4 或者 6。我们移动的方块比剩下的k个方块中的n个小,比k-n个大。如果我们下移方块,总的逆序对数量变化就是(k-n)-n=k-2n;如果我们上移方块,这个变化就是n-(k-n)=2n-k。这个变化量无关紧要,重要的是这些数都是偶数。
所以,每次移动之后,逆序对总数的奇偶性保持不变——原来是奇数的还会是奇数,原来是偶数的也还会是偶数。如果初始配置有偶数个逆序对,那么这个和在游戏中一直都会是偶数。我们不可能通过移动方块来让这个和变成奇数。同样,如果和开始是奇数,那么它也一直都会是奇数。
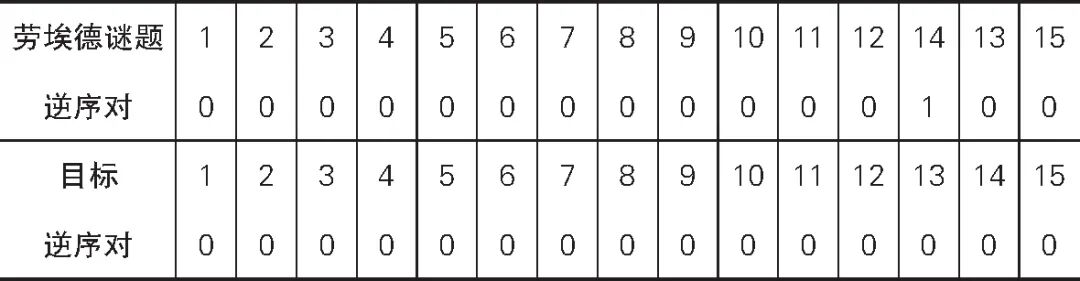
我们再来考察劳埃德谜题。他把 14 和 15 调换了顺序。在我们重新编号的例子中,调换了顺序的方块是 13 和 14。正如我们在表 2.3 中看到的,劳埃德谜题中逆序对数量是 1,而 1 是个奇数。但游戏目标是让方块按数字顺序排列,目标排列的逆序对数量是 0,而 0 是个偶数。因为游戏中逆序对数量的奇偶性不变,所以我们不可能解开劳埃德谜题并拿走 1000 美元!
表 2.3 劳埃德谜题中逆序对的数量和目标排列中逆序对数量的奇偶性不同
03 基本法则的重要性
规则决定一切。如果没有规则,那么不可能也会变成可能。看看德·摩根和达德利遇到的化圆为方者和三等分角者就知道了!在数学中,公理和定义就是基本法则。它们包括在具体问题或者定理陈述中用到的假设,也包括那些使我们得以构建坚实数学证明的逻辑规则。如果我们忽略或者改变它们,就有可能完成先前被认为不可能的任务。
如果在我们的偶数例子中可以使用除法,就能从偶数获得奇数(14÷2=7 是一个奇数)。这样,不可能也成了可能。类似地,在给定规则下,劳埃德的 15 - 数字推盘游戏是无解的。但如果我们能把方块拿出来,然后重新组装,那它就是可解的。
许多小孩子(和他们的家长)都曾用这种方法“复原”过魔方。数学中也存在这种类型的例子。欧几里得证明了三角形内角和是 180°。因此,不可能作一个内角和是其他数值的三角形。但是在 19 世纪,数学家们意识到,如果可以修改规则并且改变欧几里得的公设,他们就能创造出全新的、自洽的非欧几何体系。
这些几何体系具有奇怪的表现。例如,三角形内角和可能不是 180°。在图 2.4 左图中,我们会看到球面上的一个三角形(三边均为大圆上的弧)。这个三角形的三个角均为 90°,所以它的内角和是 270°,比 180°要大。在右图中,我们会看到一个马鞍形曲面上的三角形。这个三角形的内角和小于 180°。因此,如果改变规则,我们就能化不可能为可能。
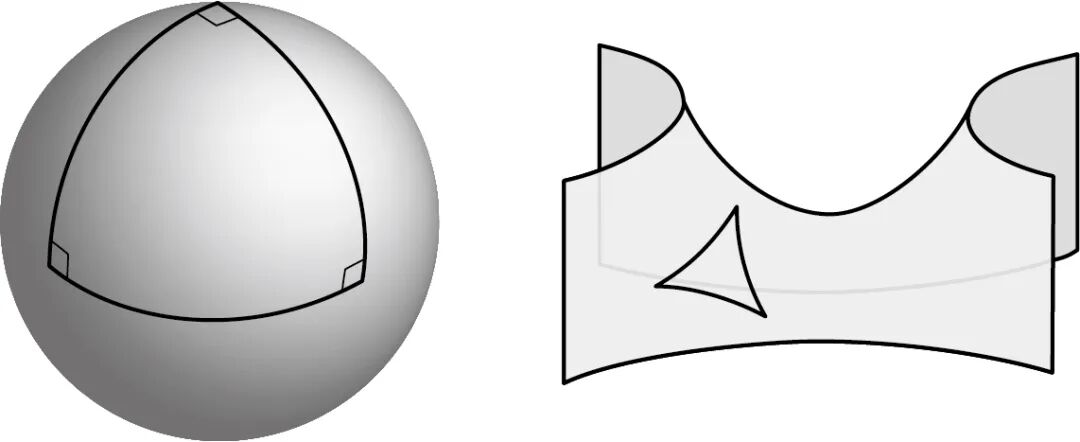
图 2.4 三角形内角和有可能大于(左)或小于(右)180°
这本书中的很多地方都将讨论,如果我们能改变规则会怎样——可能是使用额外的工具,也可能是舍弃一些工具,又或者是做一些完全不同的事情。然后我们将探究改变规则后又可以作什么图,尤其是,要解决古典问题需要做什么。
最后是一个警告:我们不能过分自信。我们确实可以肯定地说某事在数学上不可能,但是不能错误地认为这样的论证也适用于生活中的其他地方。1903 年 10 月 22 日,在莱特兄弟于北卡罗来纳州小鹰镇成功飞行还不到两个月前,约翰霍普金斯大学的数学教授西蒙·纽康(1835—1909)写了如下文字:
今天的数学家承认他们无法化圆为方、倍立方或者三等分角。类似地,我们的机械师们,会不会也最终被迫承认,在空中飞行也是人类永远无法解决的那一大类问题之一,并且不再尝试解决它?
04 闲话 九个不可能性定理
只要乐于钻研,精于实践,我们立刻就能克服困难,只要再多一点时间,就能超越认知。
——美国阿灵顿国家公墓外海蜂(美国海军工兵营)纪念碑碑文
数学中一些最伟大的定理就是关于不可能性的定理。这里我们将介绍其中最著名的九个定理。
(1)\boldsymbol{\sqrt{2}} 是无理数。 传说,梅塔庞托的希伯斯(活跃于公元前 5 世纪)是毕达哥拉斯(约公元前 570—约公元前 495)的一个追随者。他因为证明正方形的边和对角线不可公度而让他的同僚震怒。用今天的术语来说就是,他证明了 \sqrt{2} 是无理数。也就是说,我们无法找到整数 m 和 n,使得 \sqrt{2}=\dfrac{m}{n}。我们会在第 4 章深入讨论这一发现。
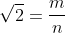
(2)费马大定理。 1637 年,皮埃尔·德·费马(1601 或 1607— 1665)在他的一本书的空白处写下了这句著名的话:“不可能把一个立方数分为两个立方数,或是把一个四次幂分为两个四次幂。更一般地,不可能把一个高于二次的幂分为两个同次幂。关于此,我发现了一种美妙证法,但这里空白太小,没法写下。”换句话说,如果 n>2 是一个整数,那么 a^n+b^n=c^n 没有正整数解。这个结论被称为费马大定理。超过三个半世纪以来,人们都无法证明它。直到 1994 年,秘密研究了 7 年的安德鲁·怀尔斯才终于证明了费马大定理。
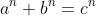
(3)哥尼斯堡七桥问题。 18 世纪中叶,普鲁士城市哥尼斯堡有七座跨越普列戈利亚河的桥(图 T.3)。当地居民在闲暇时,就会寻找一条走过每座桥刚好一次,并最终回到起点的散步路线。这一游戏被莱昂哈德·欧拉(1707—1783)得知,他在 1735 年证明了不存在这样一条路线。欧拉的方法如今被认为是图论领域的开端。
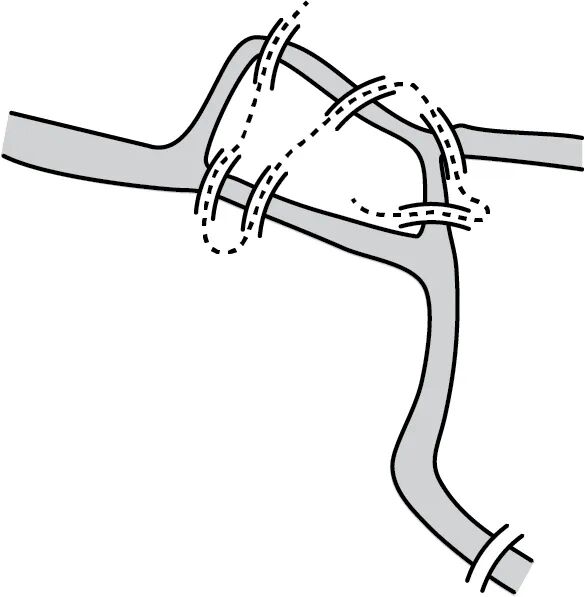
图 T.3 不能同时经过哥尼斯堡的七座桥的路线
(4)五次方程无根式解。 二次方程的求根公式算得上是高中代数课内容的巅峰了。它为求方程 ax^2+bx+c=0 的两个根提供了一种简单的计算方法。公式如下:
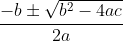
尽管复杂得多,三次方程和四次方程的根也有类似的表达方式。但是,五次或更高次方程的根无法用这样的公式来计算。特别是,多项式 x^5-x+1 有一个实数根,大约是 - 1.673 04,但我们无法用整数、四则运算以及开方来表达这个数。尼尔斯·阿贝尔(1802—1829)在 1824 年给出了这个不可能性定理的第一个完整证明。
(5)连续统不可数。 我们有十根手指。我们知道这一点,因为手指和集合 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} 中的元素可以一一对应起来。小孩子就是这样数手指的。格奥尔格·康托尔(1845—1918)推广了这一概念——用来数无穷集。如果一个集合能和正整数集 {1, 2, 3,…} 一一对应,那么我们称该集合可数无穷。整数、偶数、质数都是可数无穷集。最令人惊讶的是,有理数也是可数无穷的。但是康托尔证明了不是所有无穷集都是可数的,更大的、不可数的无穷是存在的。他证明了正整数和实数之间不存在一一对应的关系。这一发现震惊了数学界。如今它被认为是数学史上最重要的成果之一。它也是下面第 6 和第 9 个定理的核心所在。
(6)停机问题。 任何写过简单计算机程序的人都知道,存在无限循环无法停止的程序。它可能只是个重复打印简单文字(“Hello world! Hello world! Hello world!...”)的程序,也可能是程序中的一个难以察觉的漏洞。当用户输入预想之外的内容时,这个漏洞就会导致程序进入无限循环。要是有个计算机程序能判断另一个计算机程序对于特定输入会不会无限循环不是挺好的吗?不幸的是,这样的程序并不存在。1936 年,艾伦·图灵(1912—1954)证明了这个不可能性定理。该问题现在被称作停机问题。
(7)阿罗不可能性定理。 有很多著名的选举被“第三方搅局者”影响。假设候选人 A和B一对一角逐的话,A会获胜,甚至可能大胜。但如果与A有着类似政见的候选人C参加选举,某些本来会投A的人就会投C,那么这反而会让B赢得选举。所以B不是因为更受欢迎而胜选,而是因为多数投票没办法很好地适用于有三名候选人的情况。我们也有其他的投票机制,比如同意投票或者排序复选制等。每种投票机制都有其利弊。没有一种投票机制是完美的。1950 年,经济学家肯尼斯·阿罗(1921—2017)研究了排序投票制。在排序投票中,每位投票人对于候选人都有一个喜好排序。系统最后会得出一个总的候选人排名。阿罗给出了几个公平的投票机制应该具有的常识性的标准。他随后证明了不存在满足所有标准的完美投票机制。
(8)平行公设。 欧几里得用一些定义、五条公理和五条公设证明了《几何原本》中的全部定理。第五公设现在被称作平行公设,它听上去有些拗口,有些难以理解。约翰·普莱费尔(1748—1819)给出了下面这个更直观的等价版本:
“经过直线外一点有且仅有一条直线平行于已知直线。”
数百年间,数学家们曾认为平行公设是多余的,并且可以用其他四条公设推导出来。我们现在知道这是不可能的。在 19 世纪,数学家们发现了满足前四条公设,却不满足第五公设的非欧几何。在非欧几何中,普莱费尔公理并不成立。同理,第五公设也不成立。在马鞍形上,给定直线和直线外一点,有无数条经过这点的直线与已知直线不相交。在球面上,所有的线(大圆)都相交,所以经过一点不存在任何与已知直线毫无交点的直线。因为非欧几何的存在,我们知道了不可能用前四条公设推导第五公设。
(9)哥德尔不完备定理。 最后一个不可能性定理精巧、深刻,又震撼人心:无法证明的定理是存在的,即便它们是真正的数学表述。数学家们很熟悉那些看上去无法证明的猜想,例如孪生素数猜想、哥德巴赫猜想和黎曼猜想。乐观的数学家们认为它们最终都会得证。但即便它们永远不会得证,那就意味着我们不可能证明它们吗?或许吧。有可能它们可以被证明,只是数学家们还不够有创新性,没能发现证明。但它们也有可能是正确的,并且是无法证明的。在 19 世纪和 20 世纪之交,数学家们致力于为数学构建一个坚实基础——一组能推导出所有数学的定义和公理。这梦想是如此宏大,最终却又化作泡影。1931 年,库尔特·哥德尔(1906—1978)证明了不完备定理。第一不完备定理指出,在任何足够复杂的公理体系中,都存在不能被证明的真命题。在某种意义上,这是最极致的不可能性的证明!
这些数学史上的里程碑,深刻地揭示了人类理性探索的边界与可能性。想了解更多关于数学、逻辑和计算理论的精彩讨论,欢迎前往 云栈社区 交流探讨。