Time-o1损失函数：解决时序预测标签自相关与优化难问题

解决标签自相关和任务过载的双重挑战。

在时间序列预测领域，研究者们热衷于设计复杂的网络架构，从经典的 Transformer 到各类线性模型轮番登场。然而，当大家都把注意力集中在模型结构创新时，是否忽略了一个关键问题？训练这些模型时所使用的损失函数，几乎无一例外地选择了时域均方误差（TMSE），这或许正在悄悄拖累模型的最终性能。

NeurIPS 2025的最新研究揭示了TMSE存在的两大固有局限：其一，预测标签序列普遍存在自相关性，但TMSE默认各预测步相互独立，导致损失函数有偏；其二，随着预测步数增加，任务数量线性增长，优化难度显著上升。来自北京大学、小红书等机构的研究团队提出了Time-o1方法，通过巧妙的标签正交变换技术，一举解决了这两大难题，在多个主流模型上实现了显著的性能提升。

论文题目： Time-o1: Time-series Forecasting Needs Transformed Label Alignment
发表会议： NeurIPS 2025
作者单位： 小红书、浙江大学、北京大学、松鼠AI等
代码链接： https://github.com/Master-PLC/Time-o1

01 问题分析：被忽视的损失函数设计

在时间序列预测任务中，构建高精度的预测模型通常围绕两个核心问题展开：（1）如何设计神经网络架构以有效捕捉历史信息；（2）如何制定合理的损失函数以高效指导模型训练。近年来，研究重点几乎全部倾注于模型结构的创新，例如提出了形形色色的Transformer变体、线性模型等，而损失函数的设计却鲜有深入的探讨。

现有主流方法普遍采用直接预测范式。在该范式下，模型以一段历史观测为输入，通过神经网络主体提取特征，再配合一个线性输出头，一次性并行预测未来T步的标签序列。与传统的迭代预测相比，直接预测法因其并行性和效率优势而得到广泛应用。

在损失函数层面，直接预测方法几乎都选用时域均方误差（TMSE）作为优化目标，其定义如下：

L_TMSE = (1/T) * Σ_{t=1}^{T} (y_t - ŷ_t)^2

其中 y_t 是真实标签，ŷ_t 是模型预测值。然而，TMSE这类损失函数在训练时序预测模型时存在两个关键的理论缺陷，使其成为了性能进一步提升的“天花板”。

1.1 挑战一：标签自相关性导致损失函数有偏

时间序列数据的基本特性在于，任一观测值往往与其过去值高度相关，呈现显著的自相关特点。然而，TMSE在计算损失时，默认各预测步之间相互独立，完全忽略了标签序列中各时间步之间固有的自相关性。这导致TMSE作为一个损失函数在理论上是“有偏”的。具体偏差由以下定理描述：

[定理1：自相关偏差] 设标签序列 y ∈ R^T，其步间相关系数矩阵为 Σ ∈ R^{T×T}，则TMSE与真实标签的负对数似然之间的偏差为：

偏差 = (1/2) * log|Σ| + (1/2) * tr(Σ^{-1}) - T/2

其中 |·| 表示行列式，tr(·) 表示迹。当且仅当标签序列 y 的不同时间步完全不相关时（即 Σ 为单位矩阵），该偏差才会消失。现实中的时间序列显然不满足此条件。

1.2 挑战二：任务数量激增导致优化难度加大

TMSE将每个未来的预测步都视为一个独立的回归任务，这直接导致整体任务数量随着预测步数 T 线性增长。当任务数过多时，多任务学习过程中各任务的梯度方向容易产生冲突，严重影响优化的收敛过程，最终拉低模型性能。在需要长期预测的场景下，这个问题尤为突出。

02 Time-o1：在变换域定义损失函数

2.1 核心思想

Time-o1的核心思想非常巧妙：使用主成分分析（PCA），将原始的标签序列变换为一组按重要性（方差）排序的、且彼此正交的主成分。通过让模型的预测去对齐这些主成分，Time-o1能够同时解决前述两大挑战：

1. 消除自相关偏差：正交的主成分之间不相关，从根本上解决了标签自相关导致的损失函数有偏问题。
2. 降低优化难度：只需关注方差最大的前 K (K < T) 个主成分，即可捕获绝大部分信息，从而显著减少需要优化的“任务”数量。

2.2 实现流程

Time-o1的实现流程清晰，可分为以下步骤：

1. 标准化标签序列：首先对标签序列进行标准化处理，消除量纲影响。
2. 计算投影矩阵：对标准化后的标签序列执行奇异值分解（SVD），保留与最大奇异值对应的 K 个右奇异向量，拼接得到最优投影矩阵 V_K ∈ R^{T×K}。
3. 空间变换：将模型的预测序列 ŷ 及真实标签序列 y 一同变换至主成分空间：

   z = y^T V_K     # 标签主成分
   ž = ŷ^T V_K     # 预测主成分

4. 计算变换域损失：在主成分空间内计算均方误差：

   L_PCA = (1/K) * ||z - ž||_2^2

5. 目标融合：将主成分空间损失与原时域空间损失进行加权融合，平衡两者贡献：

   L_Total = α * L_TMSE + (1 - α) * L_PCA

   其中 α 为超参数。

Time-o1是一种模型无关的损失函数设计，可以即插即用地应用于各类时序预测模型，无需改动模型主体架构。

2.3 案例分析

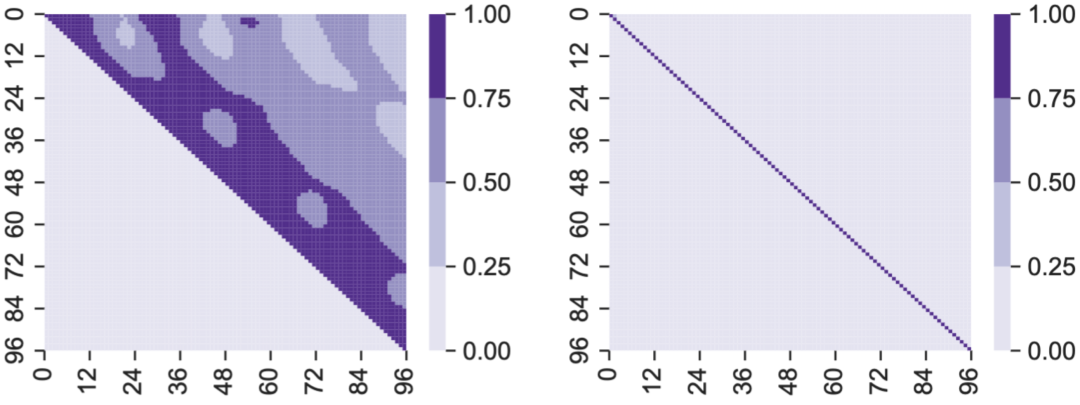
针对问题一，上图对比了原始标签序列和变换后主成分序列的自相关矩阵（热力图）。左图（原始空间）显示，大量非对角元素的值明显偏大（约50.5%超过0.25），表明标签序列存在强自相关。右图（主成分空间）的非对角元素则基本趋近于零，清晰证明了将标签变换至主成分空间可有效消除自相关性。

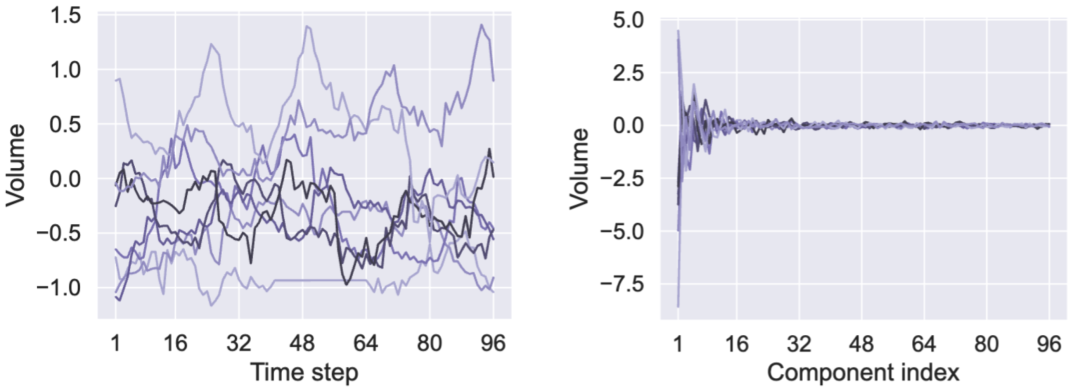
针对问题二，上图展示了原始标签与主成分的方差分布。左图中，标签序列各时间步的方差分布较为平均，意味着优化时需要对所有预测步“一视同仁”。右图中，只有前几个主成分拥有较大的方差，重要性排序分明。这表明，通过仅关注最重要的前K个主成分，我们可以在牺牲极少信息量的前提下，大幅降低优化复杂度。

03 实验结果

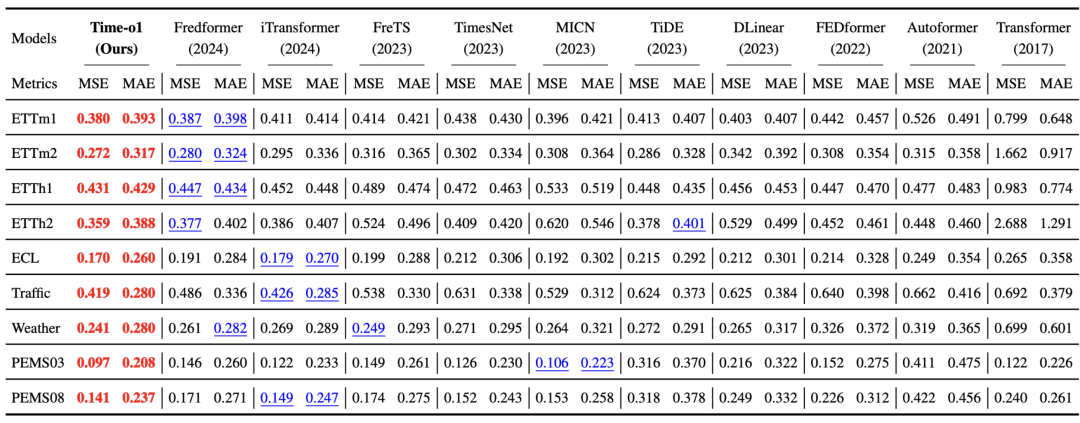
Time-o1可以显著提升预测性能。上表展示了Time-o1与近年来主流时序预测模型在多个公开数据集上的对比。以ETTh1数据集上的Fredformer模型为例，使用Time-o1损失函数（Time-o1 (Ours)）相比使用标准TMSE的Fredformer（2024），MSE指标降低了0.016（从0.447降至0.431）。在其他数据集和模型上也观察到了类似的稳定提升。这些结果有力地表明，优化损失函数所带来的性能增益，可以与改进模型架构相媲美，甚至更优。

可视化结果进一步揭示了Time-o1的优势。上图对比了使用不同损失函数的模型预测效果。虽然使用传统MSE训练的模型（DF）能够捕获序列的一般趋势，但在处理剧烈变化时（如图中100-400步内的峰值）显得力不从心，预测平滑且幅度不足。这反映了MSE在建模高方差分量时的固有不足。相比之下，Time-o1通过显式地区分和对齐这些重要的高方差主成分，其预测结果能够更准确地捕获序列中的大幅波动，拟合能力显著更强。

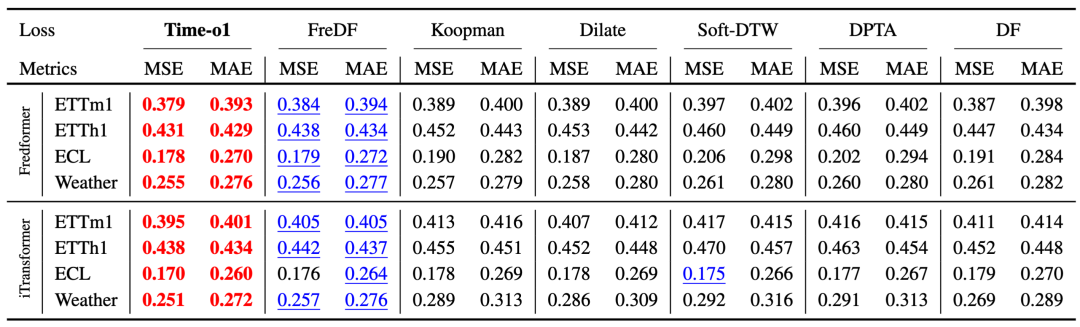
Time-o1相比其他专注于形状对齐的先进损失函数（如Dilate, Soft-DTW）也表现更佳。上表显示，这些形状对齐目标相比基础DF方法提供的性能提升非常有限。原因在于，它们既没有缓解标签相关性，也没有减少任务数量以简化优化。而Time-o1直接击中了这两个核心痛点，从而实现了整体性能的大幅跃升。

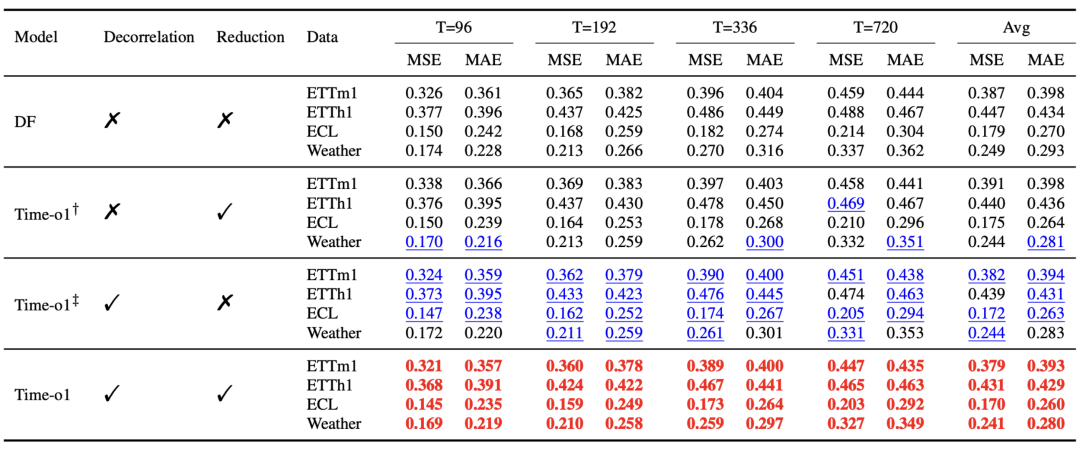
消融实验深入分析了Time-o1中两个关键组件（标签去相关Decorrelation和降维Reduction）的贡献。结果表明：仅使用去相关技术，或仅使用降维技术，相比基础DF方法都能带来改进。而将两者结合（即完整的Time-o1）取得了最佳结果，这证明了解决自相关和降低优化难度二者具有协同效应。

除了PCA，Time-o1框架也支持其他统计变换方法，如SVD、鲁棒主成分分析（RPCA）、因子分析（FA）等。上表对比了这些方法，可以看到，任何合理的变换方法相比不做变换的DF基线都有性能提升。其中，PCA因其能同时实现完美的标签正交化和有效的降维，取得了最佳的综合性能。

Time-o1的模型无关性得到了充分验证。研究团队在FredFormer、iTransformer、FreTS、DLinear等多种主流神经网络架构上进行了测试。上图的柱状图清晰显示，为这些模型换上Time-o1损失函数后（红色柱），相比其原版损失函数（蓝色柱），在绝大多数情况下都带来了MSE和MAE指标的下降。这证明了Time-o1是一种通用、有效的性能提升工具。

04 结论

这篇来自NeurIPS 2025的工作深刻地指出，时间序列预测中的损失函数设计存在两个长期被忽视的关键挑战：标签自相关导致损失函数有偏，以及任务数量过多导致优化困难。

为此，Time-o1创新性地提出了一种基于标签变换的损失函数新范式。该方法通过PCA将标签序列映射为按重要性排序的正交主成分，并引导模型预测去对齐最重要的成分，从而一举解决了上述两个挑战。

Time-o1的价值不仅在于验证了优化损失函数是提升时序预测性能的一条高效途径，与复杂的架构设计同等重要；更在于它首次将特征工程的思想创造性地应用于“标签端”，为时间序列预测乃至更广泛的回归任务领域，开辟了一个富有潜力的新研究方向。

对时间序列预测、损失函数设计或机器学习优化感兴趣的朋友，不妨访问云栈社区获取更多深度技术解析与讨论。或许，正交化的思想就是您模型性能优化的“最后一棒”。