
在量化金融领域,系统化的趋势跟随(Trend-Following)策略,尤其是基于时间序列动量(time-series momentum)的模型,一直是成熟且核心的范式。无论是CTA基金还是多资产组合,围绕“价格趋势是否会延续”这一核心问题,研究者们已经构建了大量基于单一市场自身价格历史的交易信号。然而,现实中的金融市场并非由彼此孤立的资产构成,不同市场之间往往存在着复杂的联动、传导与先行—滞后关系(lead-lag effect)。
这篇名为 《Follow the Leader: Enhancing Systematic Trend-Following Using Network Momentum》 的论文,正是从这一现实出发,提出了一种将“横截面动量溢出”概念升级为 “网络动量(Network Momentum)” 的新型趋势跟随框架,并在商品期货市场进行了实证检验。
论文的核心洞见在于:趋势不仅存在于单一市场内部,它还会沿着市场之间的结构关系进行“传染”或传播。主动捕捉这种跨市场的趋势传播模式,能够系统性地提升传统趋势策略的风险收益特征。
传统趋势策略的局限:忽略了市场间的联系
经典的趋势跟随策略,例如基于MACD或移动平均线交叉的模型,通常只以单一资产的历史价格为输入来生成信号。这类策略长期来看能产生显著的正偏度(positive skewness) 收益分布,但它们的局限性同样明显:
它们完全忽略了不同市场之间可能存在的先行—滞后关系。
已有学术研究表明,股票市场的强势表现可以在一段时间后预测公司债券、大宗商品等其他资产的收益变化。这种现象背后是信息扩散速度、投资者结构、市场流动性等基本面因素的差异。这篇论文在此基础上提出了一个更强的假设:
如果这种先行—滞后关系并非简单的点对点,而是以复杂的网络结构存在,那么用于捕捉趋势的信号本身,也应当具备“网络”属性。
方法论演进:从横截面动量到网络动量
论文的第一步并非直接构建交易策略,而是严谨地刻画市场之间的先行—滞后关系。研究者选取了28个商品期货合约作为研究对象,覆盖金属、农产品、能源和股指等主要资产类别,数据跨度从2005年至2024年。为了消除不同市场波动率水平的差异,所有价格序列首先被转化为波动率调整后的价格差值(volatility-scaled price deltas)。
随后,论文采用了多种非线性方法来识别市场间的先行关系,主要包括:
- 动态时间规整(Dynamic Time Warping, DTW)及其衍生变体
- 基于特征签名的莱维面积(Signature-based Lévy Area)方法
这些方法的优势在于不依赖于严格同步的时间轴,能够识别非线性、非对齐的趋势传播路径,从而生成一个随时间变化的领先-滞后矩阵(lead-lag matrix)。
这一步的关键目标不是预测收益,而是量化“谁在引领谁”这种结构性的市场关系。
构建市场关系网络:从矩阵到图
在获得领先-滞后矩阵后,论文引入了图学习(graph learning) 框架,将这些关系转化为一个稀疏且可解释的网络结构。在这个网络中,每个市场被视为一个节点,节点之间的加权边则代表了趋势传导的强度。通过引入正则化参数,模型可以控制网络的稀疏度,既能捕捉核心关系,又能避免对噪音的过拟合。
在此基础上,论文正式定义了网络动量特征(Network Momentum Feature):
某个市场的“网络动量”,等于其所有相邻市场的传统时间序列动量的加权和,权重则由学习得到的网络邻接矩阵决定。
这一巧妙的构造意味着:即使某个市场自身尚未形成显著的上涨或下跌趋势,只要与其紧密关联的“邻居市场”已经开始趋势性运动,这一信息就能通过网络动量特征被提前捕捉到。
表1:使用图学习计算网络动量矩阵的算法

策略构建:简约而有效的组合方式
在投资组合构建层面,论文没有追求过度复杂化,而是遵循了趋势跟随领域的成熟实践。所有原始的动量信号在进入组合前,都会经过一个反转S型响应函数(reverting sigmoid response function) 处理,用以抑制极端信号值,降低在趋势末端过度暴露的风险。论文将函数中的参数固定为 λ = √2,以确保不同信号在尺度上具有可比性。
最终的投资组合信号,由多个不同速度(回顾期)下的传统时间序列动量信号与网络动量信号等权聚合而成。
实证结果:网络动量带来了什么?
研究者采用了100组稳态自助重采样(stationary bootstrap) 样本来对真实价格序列进行模拟,并在此基础上系统比较了各种网络动量模型与基准MACD策略的表现。
表2:不同信号在各种性能指标上的表现
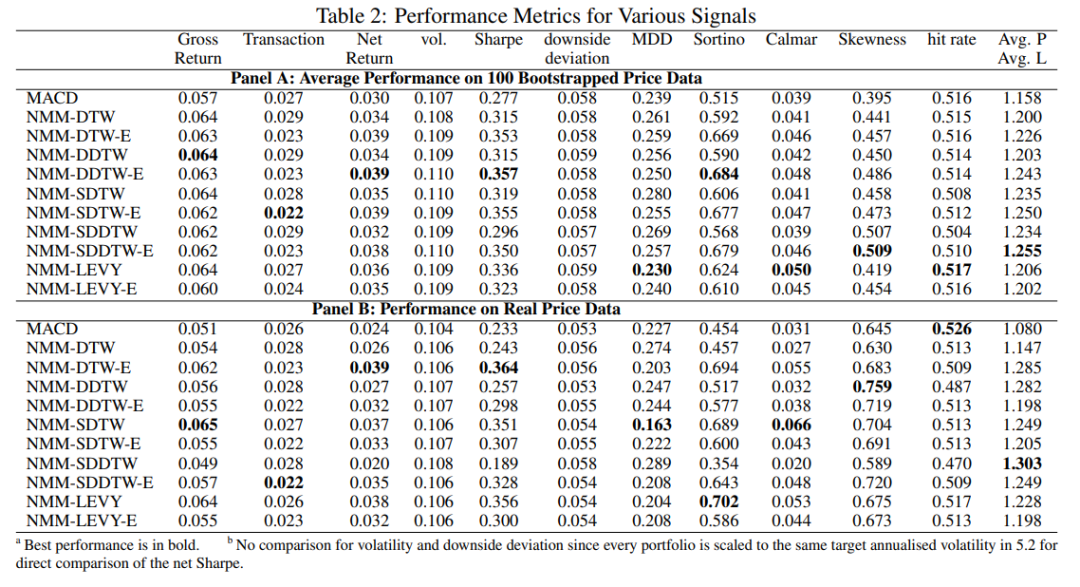
核心结论非常清晰:
- 所有网络动量模型的净夏普比率(net Sharpe ratio)中位数均显著高于传统的MACD策略。
- Wilcoxon符号秩检验的p值全部小于0.05,表明这种提升具有统计显著性。
- Kolmogorov–Smirnov检验进一步证实,网络动量模型的夏普比率分布在统计意义上优于基准策略。
这些结果强有力地表明,网络动量带来的绩效提升并非偶然,而是在统计上稳定存在的。
图1:自助数据集上各模型净夏普比率的分布
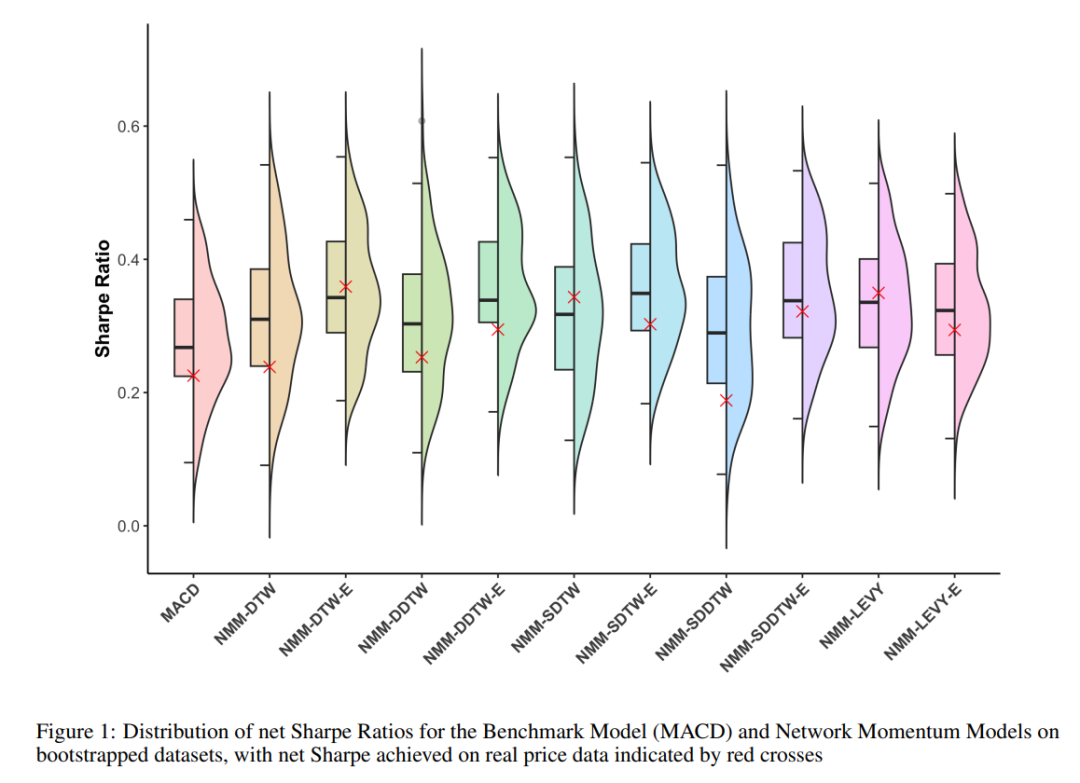
超越夏普比率:为何偏度的改善更重要?
对于趋势跟随策略而言,其魅力从来不只是更高的夏普比率,更在于其“类似期权”的收益分布结构——即显著的正偏度(赚的时候可能赚更多,亏的时候亏得有限)。论文专门分析了不同持有期下收益的偏度变化,结果发现:
- 在日频到数月的时间尺度上,网络动量模型产生的正偏度显著强于MACD基准。
- 在大约两个月的持有期附近,偏度达到峰值。
- 即使在日频层面,网络动量模型收益的负偏度程度也明显更低。
这意味着,网络动量策略在有效捕捉趋势的同时,能够更早地识别趋势启动信号,也可能更快地退出即将反转的趋势,从而整体上优化了策略的尾部风险结构。
图5:网络动量模型在不同时期的收益偏度补充图
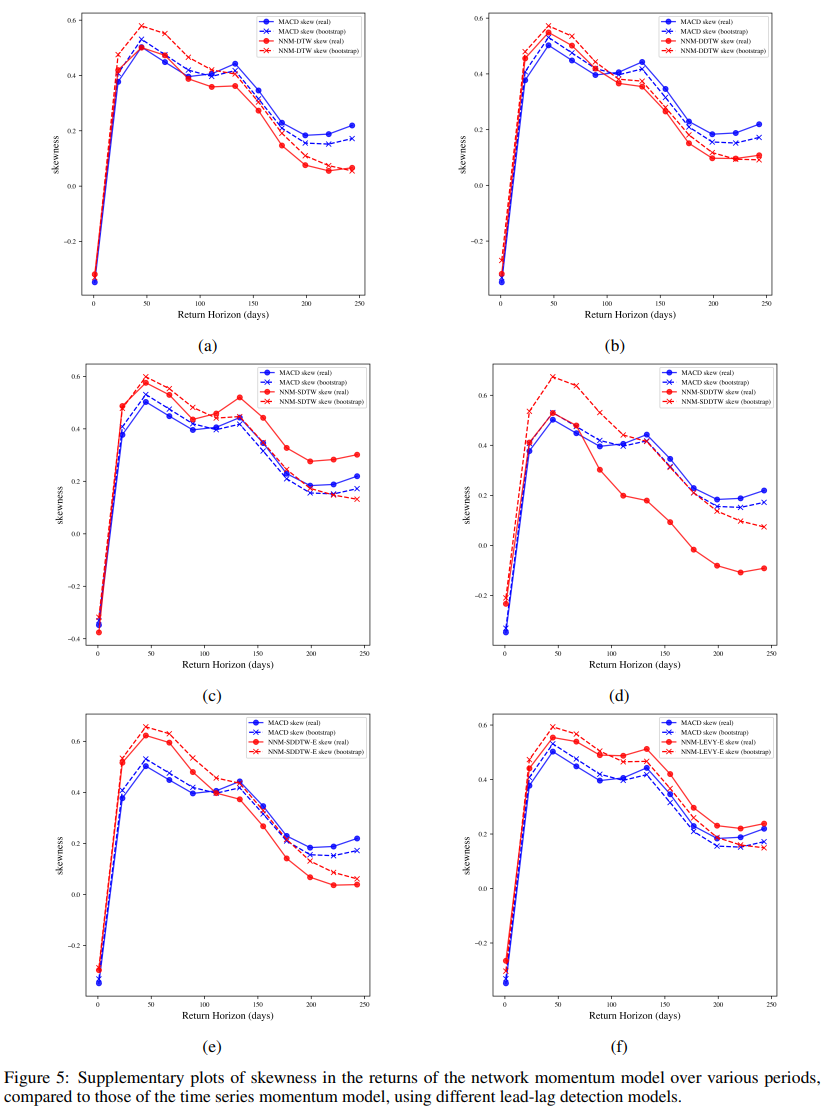
稳健性检验:结论是否普适?
一个重要的发现是,网络动量的优势并不依赖于某组特定的资产。无论是在金属、能源还是农产品等细分板块的子集上测试,网络动量模型都表现出一致的绩效提升效果。这表明,趋势沿网络结构传播是一种跨市场、跨资产类别的普遍现象,而非特定样本下的偶然结果。
总结与展望
这篇论文并没有试图用复杂的新模型完全“取代”经典的趋势跟随逻辑,而是展示了一条务实且有效的演进路径:
在保留时间序列动量核心思想的前提下,引入市场间的结构信息,可以系统性地改善趋势策略的风险收益特征。
对于量化交易与人工智能领域的研究者而言,这项工作开启了多个值得深入探索的方向:例如,如何非线性地集成多种领先-滞后检测方法;利用图神经网络(GNN)建模非对称的动态市场关系;或者针对不同频率的趋势信号,自适应地学习不同的网络结构。
论文原文链接:可通过文末“阅读原文”快速跳转。
这项研究将图学习与经典的趋势跟踪算法相结合,为处理复杂的市场联动提供了新思路。对这类时间序列分析与数据分析方法感兴趣的朋友,欢迎在云栈社区交流探讨。