完全二叉树判断算法详解：层次遍历与实战要点

在数据结构的学习与面试中，二叉树是绕不开的核心考点。其中，“完全二叉树”因其在堆等高效数据结构中的应用而备受关注。那么，什么是完全二叉树？与普通二叉树、满二叉树有何区别？更重要的是，我们如何用程序精确地判断一棵给定的二叉树是否满足完全二叉树的定义？本文将为你抽丝剥茧，从概念解析到代码实战，深入浅出地讲解判断完全二叉树的经典算法。

一、从“树”的基本概念开始

在计算机科学中，“树”是一种非常重要的非线性数据结构，其形态如同自然界倒置的树：

• 根节点：位于最顶端，是整棵树的起点，没有父节点。
• 子节点与边：从根节点向下分叉，连接的节点称为子节点，连接线称为边。
• 叶子节点：位于最末端，没有任何子节点的节点。

二、二叉树：结构规整的树

二叉树为“树”的形态增加了一层特殊的规则。

定义
每个节点最多只能拥有两个子节点，并且这两个子节点有明确的左右顺序之分——左孩子和右孩子。顺序的不同会构成不同的二叉树。

例子

• 空二叉树：一个节点都没有。
• 只有根节点的二叉树。
• 任意形态，只要满足“每个节点子节点数 ≤ 2”的树，例如根节点只有左孩子，而左孩子又只有一个右孩子。

特点

1. 节点度（子节点数）只能是0（叶子节点）、1或2。
2. 左右孩子的顺序是重要的结构特征。

三、满二叉树：二叉树的“完美形态”

满二叉树是二叉树中结构最规整、最对称的一种。

定义
除了最后一层的叶子节点外，其余所有节点都有两个子节点，并且所有叶子节点都位于同一层。

例子

• 1层满二叉树：只有根节点（1个节点）。
• 2层满二叉树：根节点有左右两个孩子（共3个节点）。
• 3层满二叉树：根节点有两个孩子，每个孩子又都有两个孩子（共7个节点）。

特点

1. 节点总数公式：若层数为 h，则总节点数为 2^h - 1。
2. 结构“饱满”，没有缺失任何可能的子节点。

四、完全二叉树：二叉树的“实用形态”

完全二叉树的定义更侧重于“编号的连续性”，是实际应用（如堆）中最常见的形态。

定义
对一棵深度为 h、有 n 个节点的二叉树，如果其每个节点的编号（按层从上到下、从左到右从1开始编号）与深度为 h 的满二叉树中编号从1到 n 的节点位置一一对应，则这棵二叉树被称为完全二叉树。

通俗理解
想象给二叉树的所有可能位置（按满二叉树的样子）排上号。如果一棵树的前 n 个位置都被节点占据，没有空缺，那么它就是完全二叉树。这导致了两个直观的视觉特征：

1. 叶子节点只出现在最后两层。
2. 最后一层的叶子节点都尽可能地靠左排列。

例子

• 任何满二叉树都是完全二叉树。
• 一个有6个节点的二叉树，如果节点占据了编号1至6的位置，而7号位置为空，那么它是完全二叉树。
• 反例：如果一棵树有节点占据了5号位置，但4号位置却是空的，这违反了“编号连续”的原则，因此不是完全二叉树。

特点

1. 可以用数组高效存储。对于数组中下标为 i（假设从1开始）的节点，其左孩子下标为 2*i，右孩子为 2*i+1，父节点为 i/2（向下取整）。

五、三者关系梳理

为了更清晰地对比，我们可以用下表来总结：

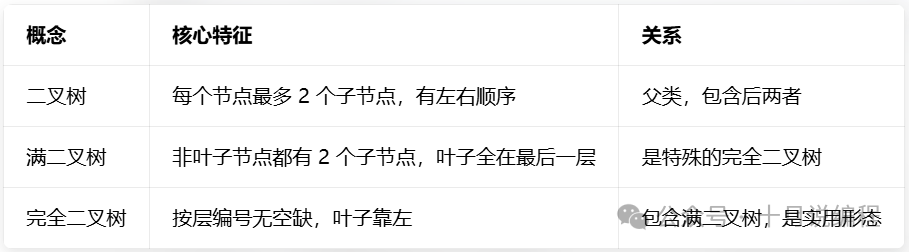
简单来说：

• 二叉树是总纲，定义了“最多两个孩子且分左右”的基本规则。
• 满二叉树是严格的完美子集，要求每一层都填满。
• 完全二叉树是宽松的实用子集，只要求“编号连续，向左靠拢”。因此，所有满二叉树都是完全二叉树，但完全二叉树不一定是满的。

六、如何用程序判断完全二叉树？

理解了定义，那么问题来了：给出一棵二叉树的节点连接关系，如何才能准确地判断它是否是完全二叉树呢？

1. 判断核心依据
根据完全二叉树“编号连续、左对齐”的特点，我们可以得出一个操作性很强的判断标准：对二叉树进行层次遍历（广度优先搜索，BFS），在遍历完所有有效节点之前，不能提前遇到空节点。

2. 算法思路详解
我们使用队列辅助进行层次遍历，并设置一个标志位来记录是否遇到了“空节点”。

1. 将根节点入队。
2. 循环执行以下步骤，直到队列为空：
   a. 取出队首节点。
   b. 如果该节点是空节点：
   • 标记“已遇到空节点”。
     c. 如果该节点是有效节点：
   • 检查“已遇到空节点”标志是否被置位。如果已置位，说明在有效节点之前出现了空缺，违反了完全二叉树的定义，立即判定为非完全二叉树。
   • 若未置位，则将该节点的左孩子和右孩子（无论是否为空）依次入队。空孩子也必须入队，因为我们需要靠它们来检测“空缺”是否提前出现。
3. 如果遍历完整棵树都未触发违规条件，则它是完全二叉树。

这个算法的精妙之处在于，它将“编号连续”的定义转换成了对遍历顺序中空节点出现位置的检验。

3. 代码实现 (C++)
以下是一个清晰的实现示例，假设输入使用 -1 表示空节点。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
struct node {
    int l, r; // 左右孩子节点编号
} a[N];
int n;
queue<int> q; // 创建队列存储节点编号

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].l >> a[i].r; // 输入

    // 利用队列模拟层次遍历
    bool isCBT = true;   // 先假设是完全二叉树
    bool metNull = false; // 是否遇到空节点标记

    // 1. 根节点（编号为1）入队
    q.push(1);

    while (!q.empty()) { // 队列不为空则继续分析
        int id = q.front(); // 取出队首节点编号
        q.pop();            // 队首出队

        if (id == -1) { // 当前出队的是空节点
            metNull = true;
            continue;
        }

        // 当前出队的是有效节点
        if (metNull) { // 但之前已经遇到过空节点了
            isCBT = false;
            break; // 提前终止，已确定不是完全二叉树
        }

        // 将左右孩子（可能是空节点）入队，以供后续判断
        q.push(a[id].l);
        q.push(a[id].r);
    }

    if (isCBT)
        cout << "YES";
    else
        cout << "NO";
    return 0;
}

4. 算法复杂度分析

• 时间复杂度 O(N)：每个节点恰好入队和出队一次。
• 空间复杂度 O(N)：队列中最多可能存储一层节点的数量，最坏情况下与节点总数 N 同阶。

5. 样例演示
假设输入格式为：第一行是节点数 n，随后 n 行每行给出一个节点的左、右孩子编号（-1 表示空）。上述算法能高效地给出判断。

例如，对于一棵结构如下的树（输入略），算法会进行BFS遍历。如果在遍历到某个有效节点时，发现队列里之前已经出列过一个空节点，则判断为 NO，否则为 YES。

总结与延伸

判断完全二叉树的层次遍历法，是将概念定义转化为可计算逻辑的典范。它不仅仅是一个面试题，其背后“利用遍历顺序检验结构性质”的思想，在处理其他树形结构问题时也很有借鉴意义。掌握好二叉树、满二叉树和完全二叉树这些基础概念，是深入学习更高级算法与数据结构的基石。希望本文的解析能帮助你彻底理解这一知识点。如果你想与其他开发者交流更多类似的技术细节，欢迎来到云栈社区探讨。