[面试题] GESP C++六级搜索算法深度解析：DFS与BFS的核心区别与实战应用

GESP C++六级官方考试大纲中，第4条考点要求掌握核心的搜索算法及其应用。

（4）掌握深度优先搜索算法（DFS）、宽度优先搜索算法（也称广度优先搜索算法，BFS）、二叉树的搜索算法的概念及应用，能够根据现实问题，选择合适的搜索算法。

搜索算法是计算机解决“怎么走”、“怎么找”问题的核心工具，也是从C++五级迈向六级、七级乃至算法竞赛的必经之路。本文将梳理这两种基础搜索算法的原理、区别及适用场景。

搜索，简单来说，就是在一个数据集合（如图、树或状态空间）中，按照某种规则寻找特定目标（如终点、最大值、解）的过程。最基础也是最重要的两种搜索策略，就是DFS和BFS。

一、深度优先搜索 (DFS)

1.1 核心概念：不撞南墙不回头

深度优先搜索(Depth-First Search, DFS) 的策略非常直观，就像走迷宫： 选定一条路，一直走下去，直到走不通（遇到死胡同或已访问过的节点）为止。一旦走不通，就回溯（Backtrack）到上一个路口，选择另一条没走过的路继续尝试。

口诀：“一条道走到黑，走不通退回来。”

• 数据结构：通常使用 栈 (Stack)。
• 实现方式：最常用 递归 (Recursion) 实现，系统会自动维护函数调用栈，这也是编程语言基础中的重要概念。

1.2 执行过程图解

假设我们要在下面的树中搜索：

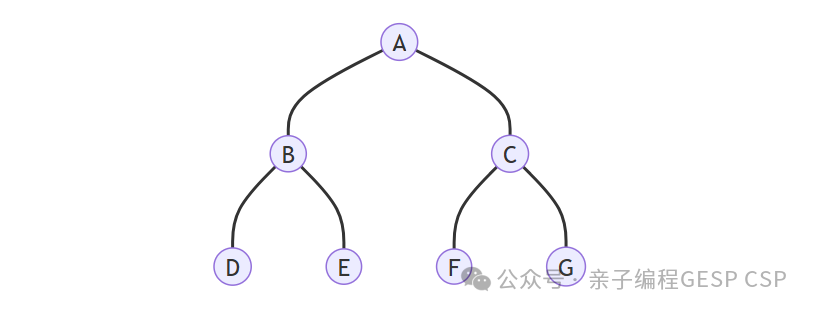
DFS 的访问顺序（假设先左后右）：

1. 从 A 出发，有路就走，先去 B。
2. 从 B 出发，先去 D。
3. D 是死胡同，回溯 到 B。
4. B 还有另一条路 E，去 E。
5. E 是死胡同，回溯 到 B，B 的路走完了，回溯 到 A。
6. A 还有另一条路 C，去 C。
7. ...以此类推。

最终序列：A -> B -> D -> E -> C -> F -> G

1.3 适用场景

• 寻找所有解：如全排列、组合生成。
• 连通性判断：判断图中两点是否连通。
• 回溯类问题：如八皇后问题、数独求解。

1.4 代码示例

#include <iostream>
#include <vector>
const int MAX_N = 1005;      // 最大节点数，根据题目范围设定
bool visited[MAX_N];         // 访问标记数组：visited[i] = true 表示节点 i 已被访问
std::vector<int> adj[MAX_N]; // 邻接表：adj[u] 保存节点 u 的所有直接邻居

// 深度优先搜索函数
void dfs(int u) {
    visited[u] = true; // 1. 标记当前节点已访问，防止重复访问导致死循环
    // std::cout << u << " "; //在此处进行节点处理逻辑（例如输出、计数等）
    // 2. 遍历节点 u 的所有相邻节点 v
    // (这里使用了 C++11 的范围 for 循环，等价于遍历 adj[u] 这个向量)
    for (int v : adj[u]) {
        // 3. 关键判断：只有未被访问过的邻居才去访问
        if (!visited[v]) {
            dfs(v); // 4. 递归调用：这是 DFS 的核心，深入下一层
        }
    }
}

代码解读：

• adj 是邻接表，是图论中最常用的存储方式。adj[1] = {2, 3} 表示节点 1 连接着节点 2 和 3。
• visited 数组至关重要，它充当“备忘录”，防止程序在环路中无限打转（比如 A 走到 B，B 又走回 A）。
• dfs(v) 的递归调用体现了“深度优先”：程序会挂起当前的 dfs(u)，优先去执行更深层的 dfs(v)，直到 v 的路走完才会回到 u。

二、宽度优先搜索 (BFS)

2.1 核心概念：层层推进，地毯式搜索

宽度优先搜索(Breadth-First Search, BFS)，也叫广度优先搜索。它的策略像平静的水面上扔一颗石子，波纹一圈圈向外扩散。

它会先访问起点的所有直接邻居（第1层），然后再访问所有邻居的邻居（第2层），以此类推。

口诀：“稳扎稳打，层层推进。”

• 数据结构：必须使用 队列 (Queue)。
• 实现方式：利用队列“先进先出”的特性，保证先遇到的节点先扩展。

2.2 执行过程图解

还是同样的树：

BFS 的访问顺序：

1. 第0层：访问起点 A。
2. 第1层：访问 A 的所有邻居 B, C。
3. 第2层：访问 B 的邻居 D, E，接着访问 C 的邻居 F, G。

最终序列：A -> B -> C -> D -> E -> F -> G

2.3 适用场景

• 最短路径问题：在无权图（每条边权重都为1）中，寻找从起点到终点的最少步数。因为是层层扩散，第一次访问到终点时，一定是最短路径。
• 层序遍历：需要按层次处理数据的场景。

2.4 代码模板 (C++)

#include <iostream>
#include <vector>
#include <queue> // BFS 核心数据结构：队列
const int MAX_N = 1005;      // 最大节点数，根据题目范围设定
bool visited[MAX_N];         // 访问标记数组：visited[i] = true 表示节点 i 已被访问
std::vector<int> adj[MAX_N]; // 邻接表：adj[u] 保存节点 u 的所有直接邻居

// 宽度优先搜索函数
void bfs(int start) {
    std::queue<int> q; // 1. 创建队列
    q.push(start);     // 2. 起点入队
    visited[start] = true; // 3. 标记起点已访问

    // 4. 当队列不为空时，循环执行
    while (!q.empty()) {
        int u = q.front(); // 5. 取出队首元素（当前要访问的节点）
        q.pop();           // 6. 队首元素出队
        // std::cout << u << " "; // 在此处进行节点处理逻辑（例如输出、计数、记录路径等）

        // 7. 遍历当前节点 u 的所有相邻节点 v
        for (int v : adj[u]) {
            // 8. 关键判断：只有未被访问过的邻居才入队
            if (!visited[v]) {
                visited[v] = true; // 9. 标记邻居已访问
                q.push(v);         // 10. 邻居入队，等待后续访问
            }
        }
    }
}

代码解读：

• 与 DFS 类似，adj 是邻接表，visited 数组用于防止重复访问。
• std::queue<int> q 是 BFS 的核心，它保证了“先进先出”的访问顺序，从而实现了“层层推进”的效果。
• 当一个节点 u 出队时，它的所有未访问过的邻居v都会被标记并立即入队。这样，所有与 u 距离相同的节点会先于距离更远的节点被处理。

三、二叉树中的搜索

二叉树是特殊的图（无环、连通），因此 DFS 和 BFS 在二叉树中有特定的对应名称。理解这些遍历方式是数据结构学习的核心内容。

3.1 DFS 与二叉树遍历

二叉树的前序、中序、后序遍历，本质上都是DFS的具体应用。

• 前序遍历：先访问根，再递归左子树，最后右子树。这就是典型的深度优先策略。

考试重点技巧：二叉搜索树 (BST) 的定向搜索

二叉搜索树（Binary Search Tree, BST）是一种有序的二叉树，其核心性质是：对于任意节点，其左子树的所有值都小于它，右子树的所有值都大于它。

如果题目明确说明是 BST，搜索目标值时千万不要盲目 DFS 遍历整棵树！

• 技巧：利用 BST “左 < 根 < 右” 的有序特性进行“剪枝”。
• 方法：
  • 目标值 < 当前节点值 -> 只搜左子树（右子树直接抛弃）。
  • 目标值 > 当前节点值 -> 只搜右子树（左子树直接抛弃）。
• 效果：这将搜索复杂度从 O(N) 降低到 O(logN)（类似二分查找），这是考试中必须具备的判断力。

3.2 BFS 与二叉树遍历

二叉树的层序遍历 (Level Order Traversal)，就是BFS的完美体现。

• 从根节点开始，一层一层打印节点值，完全符合 BFS 的逻辑。

四、如何选择合适的算法？

在考试或解决实际问题时，选择 DFS 还是 BFS，主要看目标是什么。

比较维度	DFS (深度优先)	BFS (宽度优先)
核心逻辑	回溯 (Recursion/Stack)	层层扩散 (Queue)
主要优点	代码简洁 (递归)，空间占用相对较少 (仅存路径)	一定能找到最短路径(无权图)
主要缺点	可能会在深处“迷路”，难以找到最短解	需要存储整层节点，空间消耗大
典型应用	1.找所有解(迷宫所有路径)<br>2.连通性(走不走得到)<br>3.全排列/组合	1.最短路径(迷宫最少步数)<br>2.最少操作次数<br>3.层序遍历

4.1 实例判断

案例 1：迷宫最短步数

• 问题：在一个的迷宫中，从起点 'S' 走到终点 'E'，每次只能走上下左右，问最少走几步？
• 选择：BFS。
• 理由：关键词是“最少步数”。BFS 保证第一次搜到终点时就是最短路径，而 DFS 搜到的第一条路不一定是最短的。

案例 2：迷宫逃脱

• 问题：在一个复杂的迷宫中，判断是否存在一条路能走到终点，不需要最短，只要能到就行。
• 选择：DFS。
• 理由：DFS 代码写起来通常比 BFS 短，且不需要维护队列，递归实现非常方便。

案例 3：走马观花

• 问题：二叉树的层序遍历，要求输出第一行、第二行...
• 选择：BFS。
• 理由：层序遍历的定义就是 BFS。

五、总结

• DFS 像钻头，一头扎到底，适合找可行解、遍历、回溯，是许多算法问题的基础。
• BFS 像雷达，一圈圈扫描，适合找最短路、分层处理。
• 在二叉树中，DFS 对应前/中/后序遍历，BFS 对应层序遍历。

掌握了这两个算法，你就拥有了在复杂数据结构中“寻宝”的指南针。