行列式是线性代数中的核心概念之一,理解其定义与计算方法是学习后续内容的关键。本文将从三阶行列式出发,逐步深入到n阶行列式的通用定义,并讲解其计算方法与特殊形式。
三阶行列式的展开
一个三阶行列式表示为一个3x3的矩阵:

其值可以通过“按行展开”的方式计算:从每一行、每一列中恰好选取一个元素相乘,总计有 3! = 6 种不同的取法。展开后的表达式为:
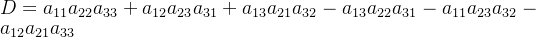
那么,如何确定每一项前面的正负号呢?其规则可总结为以下几点:
- 行标保持自然顺序(即按第一行、第二行、第三行选取)。
- 选取的三个元素必须来自不同的行和不同的列。
- 列标(即元素所在的列序号)取所有可能的排列。
- 符号由列标排列的逆序数的奇偶性决定:逆序数为偶数时取正号(
+),为奇数时取负号(-)。
n阶行列式的定义
将三阶行列式的思想推广,即可得到n阶行列式的定义。一个n阶行列式对应一个n×n的矩阵:
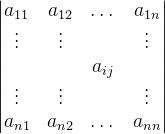
其中,元素 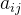 的下标 的下标i表示行标,j表示列标。
按行展开定义法
n阶行列式最常用的定义方式是按行(或按列)展开,其公式如下:
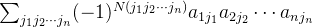
这个公式的含义是:
- 行标取自然顺序(1, 2, …, n)。
- 列标
(j₁, j₂, …, jₙ) 取1到n的所有n!种排列。
- 从不同的行和列中取出
n个元素 a_{1j₁}a_{2j₂}...a_{njₙ} 相乘,构成一项。
- 该项的符号由列标排列
(j₁, j₂, …, jₙ) 的逆序数 N(j₁j₂…jₙ) 决定,即 (-1)^N。
掌握行列式的计算,对于理解矩阵性质和求解线性方程组至关重要,这也是许多算法与数据结构问题(如计算几何、图形变换)的数学基础。
计算实例分析
为了加深理解,我们来看两个具体的计算例子。
例一:对角矩阵的行列式
计算下列4阶对角矩阵的行列式:
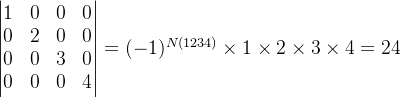
分析与解:
按行展开公式,只有列标排列为(1,2,3,4)时,选取的元素才全部不为零(即主对角线上的元素)。其他任何列标排列都会导致至少有一个因子为0,因此整个项为0。
所以,行列式的值就是 (-1)^(N(1234)) × 1 × 2 × 3 × 4 = 1 × 24 = 24。这验证了对角矩阵的行列式等于其主对角线元素的乘积。
例二:特殊稀疏矩阵的行列式
计算下列4阶行列式:
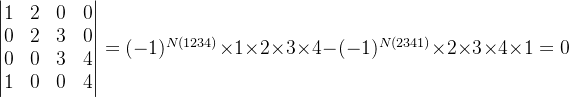
分析与解:
观察矩阵,每行每列恰好有两个非零元素。按第一行展开:
- 若第一行取
a₁₁=1,则后续行只能沿着“对角线”方向取a₂₂=2, a₃₃=3, a₄₄=4,对应列标排列为(1,2,3,4)。
- 若第一行取
a₁₂=2,则后续行只能取a₂₃=3, a₃₄=4, a₄₁=1,对应列标排列为(2,3,4,1)。
其他取法都会导致出现0因子。因此,行列式只有两项:
D = (-1)^(N(1234))×1×2×3×4 + (-1)^(N(2341))×2×3×4×1 = 24 - 24 = 0。
两类特殊行列式
掌握特殊行列式的结论能极大简化计算。
1. 三角行列式
上三角、下三角以及对角行列式的值,均等于其主对角线上所有元素的乘积。
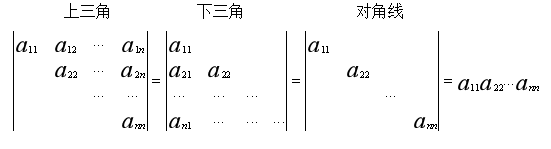
2. 副对角行列式
副对角线(从右上到左下)行列式的值,等于副对角线上元素的乘积,再乘以一个由阶数n决定的符号因子。
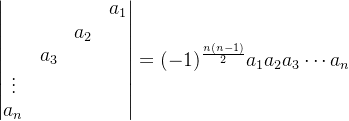
其中,符号 (-1)^(n(n-1)/2) 由逆序数 N(n, n-1, …, 2, 1) = n(n-1)/2 决定。 |