线性代数的核心：矩阵运算与向量空间结构的本质解析

在数学的广阔天地中，线性代数远不止是数字的排列与计算。它为我们提供了一套精妙的语言，用以描述和理解多维空间、向量关系以及线性变换。这套语言是现代科学、工程、数据科学与人工智能等领域的基石。矩阵的出现，使得这些抽象的概念得以具体化、可运算、可计算，从而被广泛应用到解决实际问题的方方面面。那么，矩阵是否就是线性代数的全部？我们能否简单地将线性代数等同于矩阵运算的学科？

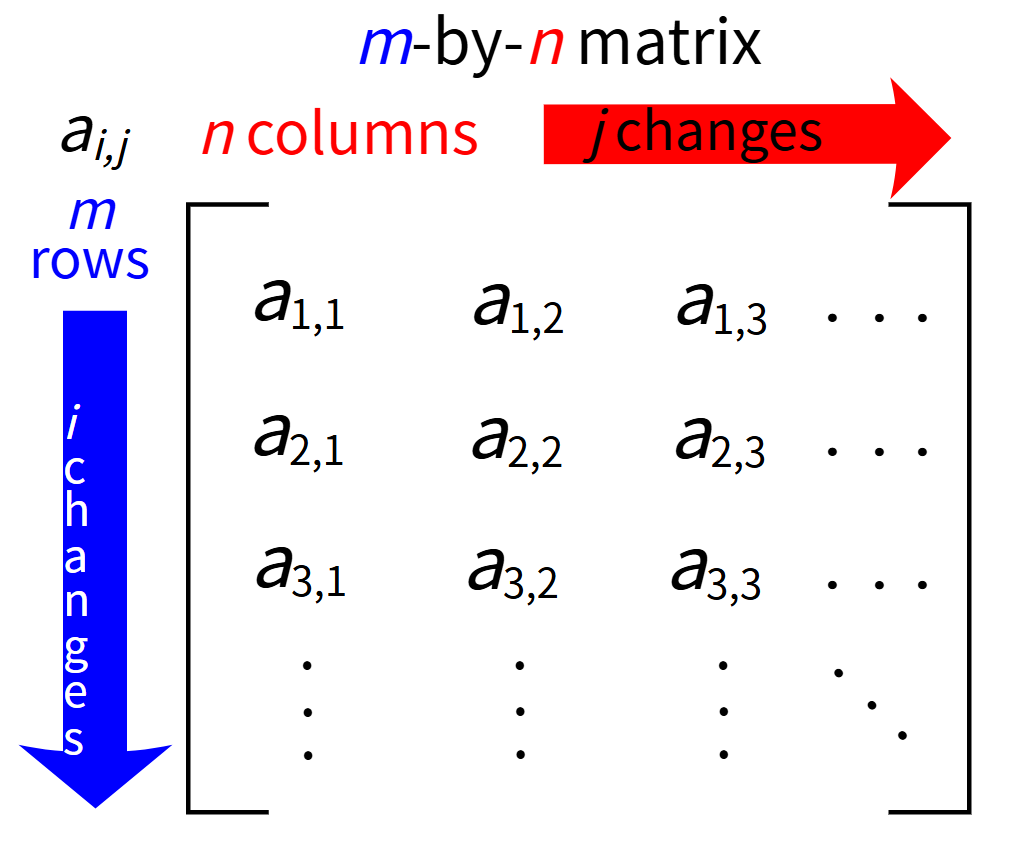
1 线性代数的基本概念

线性代数作为现代数学的重要支柱，其研究对象——向量空间与线性映射——构成了理论体系的核心。理解线性代数，必须从这些根本概念入手，它们不仅是理论的起点，也是矩阵得以引入和应用的根本背景。

1.1 向量与向量空间

向量是线性代数最基本的元素。在几何视角下，向量是具有大小和方向的量；而在更现代的代数观点中，向量被广义地定义为可以进行线性组合的任何对象，它可以是有序数组、多项式，甚至是函数。向量空间则是满足特定运算公理（封闭性、结合律、交换律、存在零元与逆元等）的向量集合。

在向量空间中，线性组合是核心操作：给定一组向量和标量，其线性组合为 。这一操作直接引出了基、维数和子空间等关键概念。

1.1.1 基与维数

基是一组线性无关且能生成整个向量空间的向量。空间的维数则由基中向量的个数决定。任何向量在给定基下都有唯一的坐标表示，这为用数组（即向量坐标）描述抽象对象奠定了基础。

1.1.2 子空间

子空间是向量空间的一个子集，并且自身也构成一个向量空间。例如，矩阵的行空间、列空间和零空间都是重要的子空间，它们揭示了矩阵的深层结构。

1.1.3 范数与内积空间

为了赋予向量空间几何意义，我们引入范数来度量“长度”，引入内积来度量“夹角”和“正交性”。满足内积公理的空间称为内积空间，它为特征值分解等高级分析提供了理论土壤。

1.2 线性映射与线性变换

线性映射是连接两个向量空间并保持加法和数乘结构的桥梁。它是研究向量空间关系的核心工具。

1.2.1 核与像

线性映射的核是所有映射到零向量的输入集合，反映了映射的“信息损失”方向。像则是所有可能输出结果的集合。秩-零度定理揭示了它们维度之间的关系：dim(核) + dim(像) = dim(定义域)，这是分析线性系统的基础。

1.2.2 矩阵表示的前提

当我们为向量空间选定一组基后，抽象的线性映射就可以用一个具体的矩阵来表示。矩阵的每一列，本质上就是定义域基向量被映射后，在值域基下的坐标。这使得对映射的研究转化为对矩阵的运算。

1.3 线性代数抽象与结构理解

线性代数的精髓在于其对结构的关注，而非具体的数值计算。它通过子空间、基、维数、核、像等概念，构建了一套研究多维系统和线性关系的统一理论框架。这个框架不仅适用于有限维，也能扩展到函数空间等无限维场景，矩阵则是这个理论在有限维情况下的完美“代言人”和计算工具。

2 矩阵与线性代数的关系

矩阵是线性代数中最具象、最便于计算的对象。它的核心价值在于，它是抽象线性映射在有限维空间中的具体化身，是连接理论与计算的枢纽。

2.1 矩阵表示线性映射

在选定基的前提下，一个线性映射唯一地对应一个矩阵。具体来说，矩阵乘以一个坐标向量，其结果就是该向量所代表的原始向量经过映射后在新基下的坐标。这种表示将抽象的变换关系转化为具体的代数运算，使得旋转、缩放、数据降维等操作得以用计算机高效实现。

2.2 矩阵运算与线性代数结构

矩阵的基本运算直接反映了线性代数的核心结构：

• 矩阵加法对应线性映射的叠加。
• 矩阵乘法对应线性映射的复合。
• 矩阵的逆对应可逆线性映射。
• 矩阵的转置与对偶空间上的映射相关。
• 行列式则描述了线性变换对空间体积的缩放比例。

因此，矩阵运算并非凭空定义，而是线性代数内在结构的自然体现。

2.3 矩阵的理论与计算意义

矩阵扮演着双重角色：在理论层面，通过分析矩阵的秩、特征值等性质，可以反推其对应线性映射和向量空间的结构；在计算与应用层面，它使得求解线性方程组、进行特征分解、实现主成分分析（PCA）等成为可能，是连接抽象理论与工程实践的桥梁。

3 矩阵在理论与应用中的作用

3.1 理论层面

从纯粹的理论角度看，线性代数的核心是向量空间和线性映射的抽象公理体系。矩阵只是有限维情况下的一个便利表示。在无限维空间（如量子力学中的函数空间）中，线性算子往往无法用有限矩阵完全描述。因此，矩阵是工具，而线性结构本身才是核心。

3.2 应用层面

在实际应用中，矩阵无疑是无可争议的核心工具。无论是图形渲染、物理模拟，还是机器学习中的模型训练，最终都落回到高效的矩阵运算上。然而，指导这些应用设计的底层逻辑，仍然是线性代数关于空间、变换和分解的抽象思想。矩阵是思想的“执行者”。

4 矩阵的结构分析与线性代数思维

矩阵本身也蕴含着丰富的结构信息，分析这些结构是理解线性代数思维的关键。

4.1 行空间、列空间与秩

矩阵的行向量生成行空间，列向量生成列空间，它们的维度相等，即为矩阵的秩。秩衡量了线性映射的“信息容量”或矩阵的“有效维度”。

4.2 零空间与秩-零度定理

零空间是齐次方程 Ax=0 的所有解构成的子空间。秩-零度定理 rank(A) + nullity(A) = n（n为列数）完美体现了线性系统的约束关系与自由度的分配，是结构性思维的典范。

4.3 特征值与特征向量

特征方程 Ax = λx 寻找的是在变换 A 下只发生伸缩而不改变方向的特殊向量。特征分解（对角化）将复杂的矩阵作用分解为沿独立方向的简单缩放，在系统稳定性分析、振动模式研究及大数据降维中至关重要。

5 高维与抽象空间中的矩阵

在无限维的泛函分析中，核心研究对象是线性算子，矩阵退化为一种有限维逼近工具（如有限元方法）。这再次说明，矩阵是处理有限维问题或进行数值逼近的强大工具，但线性代数的理论核心——对线性算子和函数空间结构的研究——超越了矩阵的范畴。

6 线性代数的核心理解框架

综上，我们可以建立一个多层次的认知框架：

1. 核心本质：向量空间的结构（线性组合、基、维数、子空间）与线性映射的性质（可逆性、秩、核、像）。
2. 核心工具/表示：在有限维情形下，矩阵是表达和计算上述核心本质的完美工具与统一语言。
3. 核心思维：通过分解（如SVD）、降维、寻找不变子空间（特征空间）等方式，理解和简化复杂线性系统。

7 结论

矩阵无疑是线性代数中最重要的计算工具和表示形式，在有限维世界中几乎不可或缺。然而，线性代数的核心灵魂在于其关于向量空间和线性映射的抽象理论体系。矩阵是这一抽象理论在计算维度的延伸和实现。将线性代数仅仅等同于矩阵运算是片面的；真正的掌握，意味着既能运用矩阵工具解决实际问题，又能理解其背后深刻的抽象结构。这二者相辅相成，共同构成了线性代数的完整图景。