快慢指针判环详解：LeetCode141环形链表（C++）

本文介绍一种检测链表是否存在环的高效方法：快慢指针（Floyd 判圈）。该方法在不额外占用空间的前提下，可在 [O(n)] 时间复杂度内完成判断，适用于面试与工程中对链表结构的健壮性检测。

在学习本题前，建议先补齐基础的算法/数据结构知识点（链表、指针移动、复杂度分析）。

题目描述

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则该链表中没有环。

示例

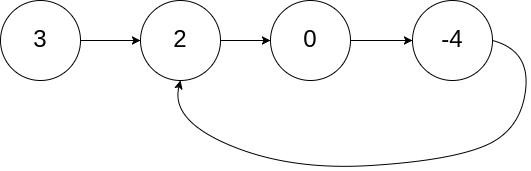
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

思路解析：快慢指针判环

核心思想是用两个指针以不同速度在链表上移动：

• slow：每次走 1 步
• fast：每次走 2 步

若链表存在环，fast 终将追上 slow，两者会在环内某个节点相遇；若不存在环，fast 会先到达 nullptr，循环结束。

进阶也建议掌握：  

• 为什么有环时快慢指针一定会相遇  
• step=2 能相遇，那么 step=n（如 n=3）是否也能相遇  
• 如何找到环的入口节点

参考代码（C++）

注意：这里 fast 从 head->next 开始，是一种常见写法，可避免初始即 slow==fast 的干扰判断。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (head == nullptr) {
            return false;
        }
        ListNode * slow = head;
        ListNode * fast = head->next;  // fast指针要这么写
        while (fast && fast->next) {
            // 慢指针每次走一步，快指针每次走两步
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针能相遇就代表有环
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }
};

复杂度

• 时间复杂度：[O(n)]
• 空间复杂度：[O(1)]

如果你在实现中遇到空指针判断、边界条件处理等问题，建议回顾 C++ 指针与链表遍历的细节，这类问题在链表题中非常高频。