LeetCode子数组算法精讲：从组合总和到滑动窗口的解题攻略

解题核心思路

面对数组子数组相关的问题时，我们可以根据子数组的特性，快速锁定解题方向：

1. 不连续子数组：通常采用回溯（DFS） 或动态规划（DP） 来求解。
2. 连续子数组：通常采用滑动窗口、前缀和或动态规划来求解。

掌握这一基本分类，能帮助我们在算法与数据结构的学习中快速找到解题入口。

LeetCode不连续子数组问题精解

39. 组合总和 (Combination Sum)

问题描述

给定一个无重复元素的数组 candidates 和一个目标数 target。找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

说明：解集不能包含重复的组合。

示例：

输入：candidates = [2,3,6,7], target = 7
输出：[[7], [2,2,3]]

解题思路

由于元素可以无限次选取，无法用常规的动态规划直接枚举所有组合。本题适合使用深度优先搜索（DFS/回溯法） 来解决。

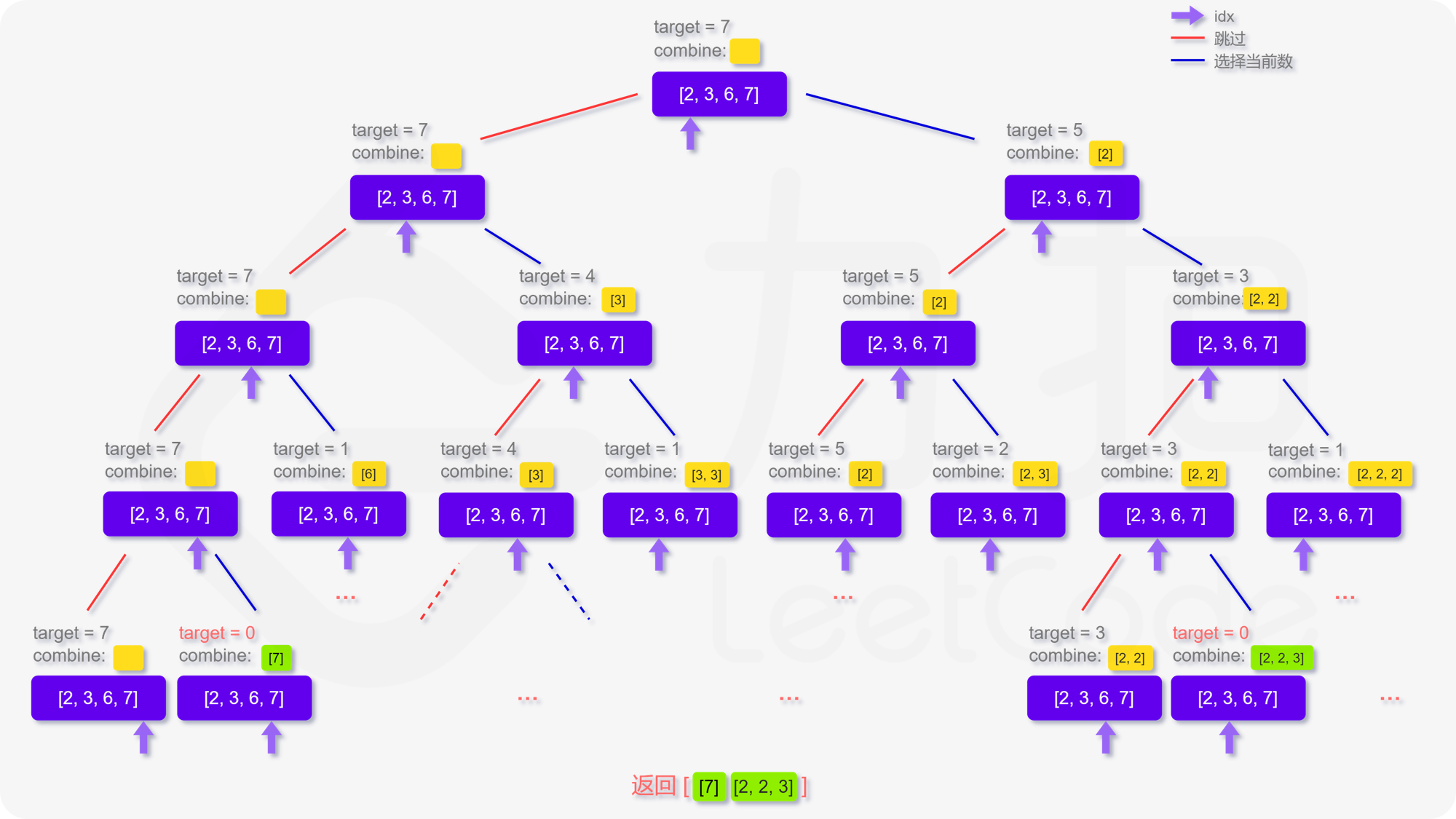
我们可以将搜索过程想象成遍历一棵决策树。对于数组中的每个元素，我们面临两个选择：

1. 跳过当前元素，从下一个元素开始新的搜索。
2. 选择当前元素，如果剩余目标值 target 仍大于等于当前元素值，则可以继续从当前元素开始搜索（因为可重复选取）。

递归终止条件：

1. 遍历完所有候选元素。
2. 当前组合的和恰好等于 target，将此组合加入结果集。

下图清晰地展示了以 [2,3,6,7]，target=7 为例的递归决策过程：

参考代码

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        dfs(candidates, target, 0);
        return res;
    }

    void dfs(vector<int>& cands, int target, int idx) {
        if (idx == cands.size()) return;
        if (target == 0) {
            res.emplace_back(com);
            return;
        }
        // 选择1：跳过当前元素
        dfs(cands, target, idx + 1);
        // 选择2：使用当前元素（前提是剩余目标值足够）
        if (target >= cands[idx]) {
            com.emplace_back(cands[idx]);
            dfs(cands, target - cands[idx], idx); // 注意idx不变，可重复选取
            com.pop_back(); // 回溯
        }
    }
private:
    vector<vector<int>> res;
    vector<int> com;
};

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        def dfs(target, idx):
            if idx == len(candidates):
                return 
            if target == 0:
                res.append(com[:]) # 注意使用拷贝
                return 
            # 跳过当前元素
            dfs(target, idx + 1)
            # 使用当前元素
            if target >= candidates[idx]:
                com.append(candidates[idx])
                dfs(target - candidates[idx], idx) # idx不变
                com.pop()
        res, com = [], []
        dfs(target, 0)
        return res

复杂度分析

• 时间复杂度：最坏情况下，递归树深度之和很大，与解的数量相关。
• 空间复杂度：O(target)，最坏情况下递归深度为 target（每次只减1）。

40. 组合总和 II (Combination Sum II)

问题描述

与39题不同，本题给定数组 candidates 中可能包含重复数字，且每个数字在每个组合中只能使用一次。同样需要找出所有和为 target 的唯一组合。

示例：

输入: candidates = [10,1,2,7,6,1,5], target = 8
输出: [[1,1,6], [1,2,5], [1,7], [2,6]]

解题思路

本题是经典的回溯+剪枝问题。关键在于如何处理重复元素导致的重复组合。

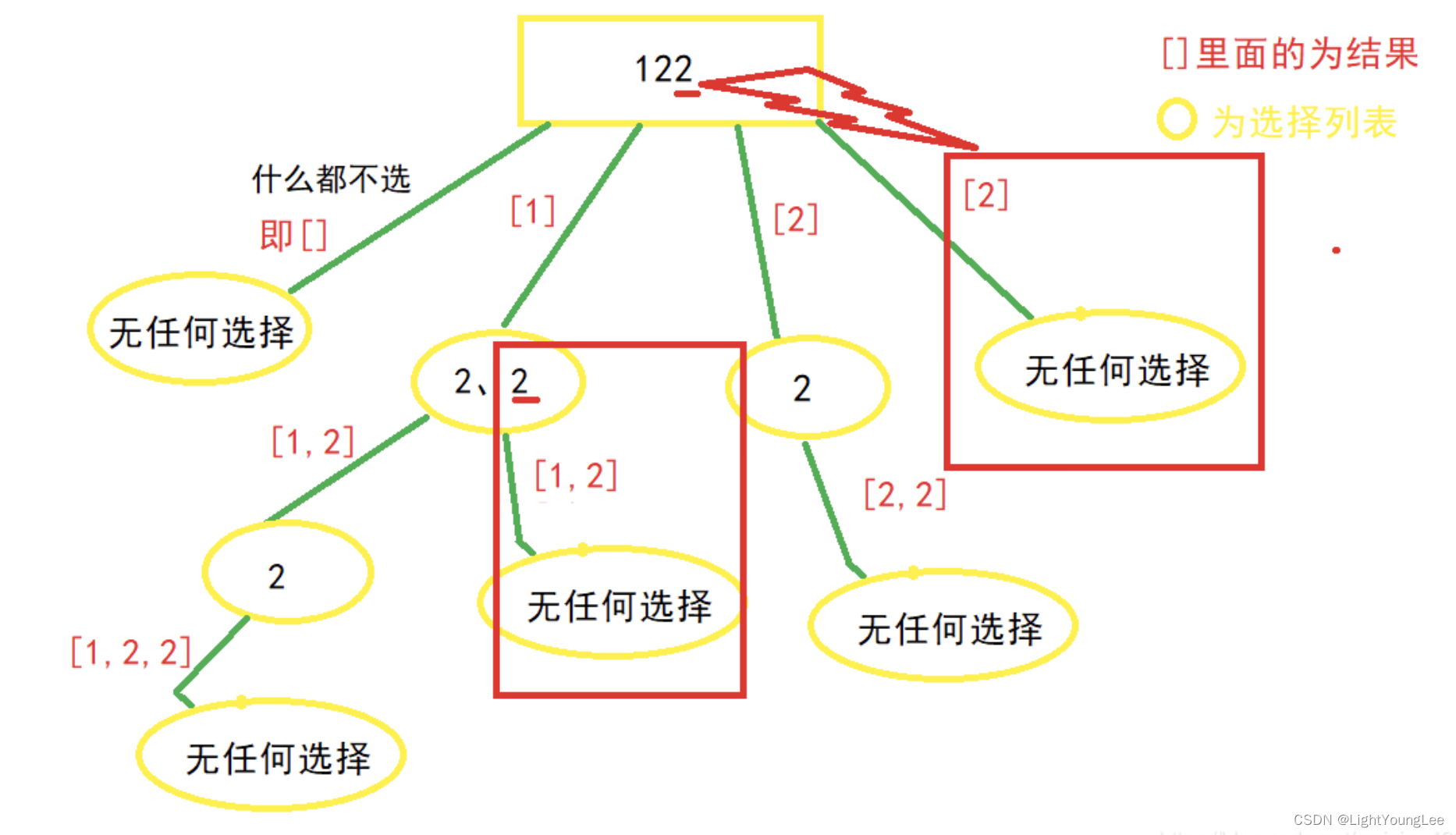
1. 排序：首先对数组进行排序，使相同元素相邻，便于后续剪枝。
2. 回溯搜索：在每一层递归中遍历候选元素。
3. 剪枝去重：在同一层递归（即同一个start位置开始的循环）中，如果当前元素与前一个元素相同，则跳过，避免产生重复组合。注意，不同递归层之间的相同元素是允许的（例如 [1,1,6] 中的两个1）。

下图展示了数组 [1,2,2] 的回溯树，其中红色框部分为被剪枝的重复搜索路径：

参考代码

class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        dfs(candidates, target, 0);
        return result;
    }
    void dfs(vector<int>& candidates, int target, int start) {
        if (target == 0) {
            result.emplace_back(path);
            return;
        }
        for (int i = start; i < candidates.size() && target - candidates[i] >= 0; ++i) {
            // 关键剪枝：同层重复元素跳过
            if (i > start && candidates[i] == candidates[i - 1]) continue;
            path.emplace_back(candidates[i]);
            dfs(candidates, target - candidates[i], i + 1); // i+1，每个数只用一次
            path.pop_back();
        }
    }
private:
    vector<vector<int>> result;
    vector<int> path;
};

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        res, path = [], []
        def backtrack(start, target):
            if target == 0:
                res.append(path[:])
                return
            for i in range(start, len(candidates)):
                if target < candidates[i]:
                    break
                # 同层剪枝
                if i > start and candidates[i] == candidates[i-1]:
                    continue
                path.append(candidates[i])
                backtrack(i + 1, target - candidates[i])
                path.pop()
        backtrack(0, target)
        return res

复杂度分析

• 时间复杂度：O(n * 2ⁿ)，回溯算法的一个宽松上界。
• 空间复杂度：O(n)，递归栈深度。

46. 全排列 (Permutations)

问题描述

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例：

输入: [1,2,3]
输出: [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]

解题思路

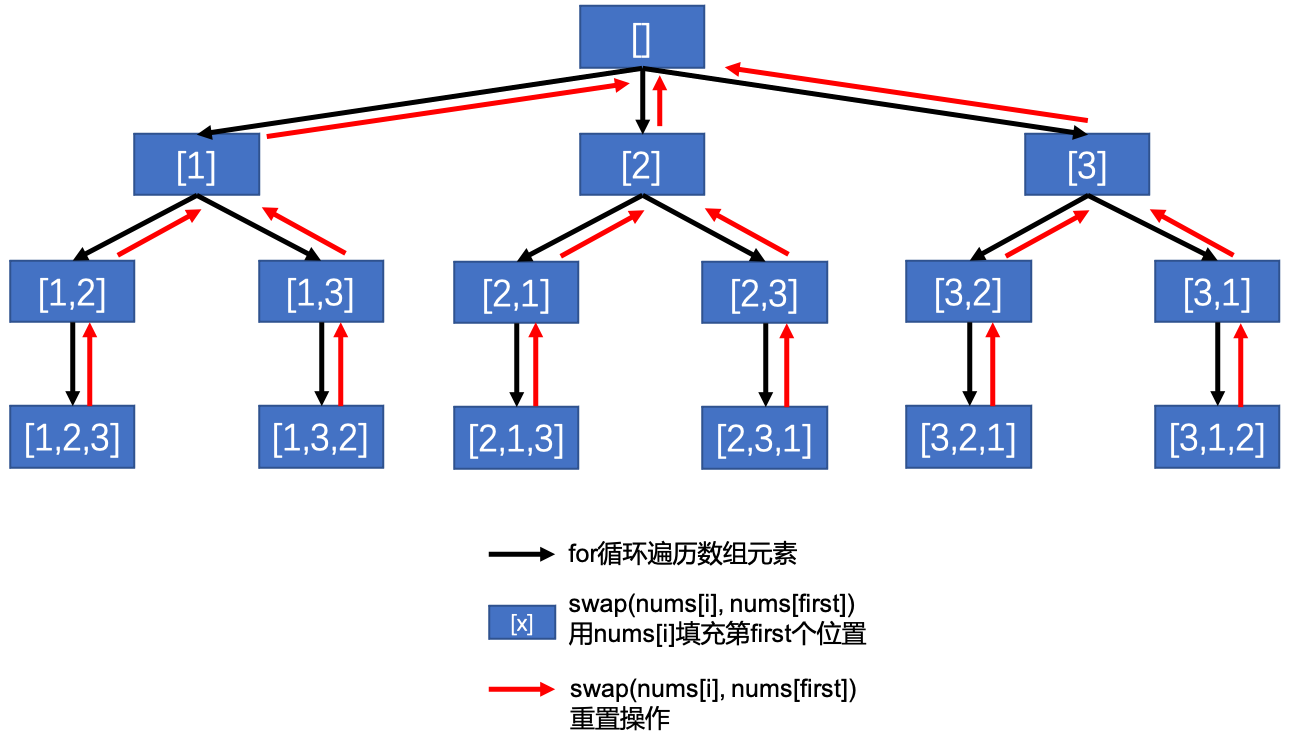
采用回溯法。核心思想是：通过交换数组中的元素来生成不同的排列。
从索引 first 开始，将其与索引 first 及其之后的所有元素依次交换，固定 first 位置的元素，然后递归地对 first+1 之后的子数组进行全排列，递归返回后再交换回来（回溯）。

下图展示了 [1,2,3] 的全排列生成树：

参考代码

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        backtrack(0, nums);
        return res;
    }
    void backtrack(int first, vector<int>& nums) {
        if (first == nums.size()) {
            res.emplace_back(nums);
            return;
        }
        for (int i = first; i < nums.size(); ++i) {
            swap(nums[i], nums[first]);   // 放置元素 nums[i] 到 first 位置
            backtrack(first + 1, nums);   // 递归生成后续排列
            swap(nums[i], nums[first]);   // 回溯，恢复原状
        }
    }
private:
    vector<vector<int>> res;
};

对于此类排列组合问题，无论是使用Python还是C++，回溯的框架都是相通的。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def backtrack(first):
            if first == n:
                res.append(nums[:])
            for i in range(first, n):
                nums[first], nums[i] = nums[i], nums[first]
                backtrack(first + 1)
                nums[first], nums[i] = nums[i], nums[first]
        n = len(nums)
        res = []
        backtrack(0)
        return res

复杂度分析

• 时间复杂度：O(n * n!)，共有 n! 种排列，每种排列生成需要 O(n) 时间。
• 空间复杂度：O(n)，递归栈深度。

78. 子集 (Subsets)

问题描述

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。

示例：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

解题思路

回溯法的经典应用。我们可以定义一个回溯函数，参数 start 表示当前选择的起始位置。在每一层递归中，我们将当前路径加入结果集（因为所有路径都是子集），然后从 start 开始遍历，将元素加入路径，递归进入下一层（起始位置+1），最后回溯。

回溯算法的通用流程可以概括为下图：

参考代码

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(0, nums);
        return res;
    }
    void backtrack(int start, vector<int>& nums) {
        res.emplace_back(path); // 当前路径就是一个子集
        for (int i = start; i < nums.size(); ++i) {
            path.emplace_back(nums[i]);
            backtrack(i + 1, nums); // 从下一个元素开始
            path.pop_back();
        }
    }
private:
    vector<vector<int>> res;
    vector<int> path;
};

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res, path = [], []
        def backtrack(start):
            res.append(path[:])
            for i in range(start, len(nums)):
                path.append(nums[i])
                backtrack(i + 1)
                path.pop()
        backtrack(0)
        return res

复杂度分析

• 时间复杂度：O(n * 2ⁿ)，共有 2ⁿ 个子集，生成每个子集需要 O(n) 时间。
• 空间复杂度：O(n)，递归栈深度。

90. 子集 II (Subsets II)

问题描述

与78题不同，本题中数组 nums 可能包含重复元素。请你返回所有可能的子集，且解集中不能包含重复的子集。

示例：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

解题思路

在78题子集问题的基础上，增加了“去重”的要求。解决方法与“40.组合总和II”类似：

1. 排序：使相同元素相邻。
2. 剪枝：在同一层递归的遍历中，如果当前元素与前一个元素相同，则跳过，以避免生成重复的子集。

下图以 [1,2,2] 为例，展示了剪枝过程（红框部分被跳过）：

参考代码

class Solution {
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        backtrack(0, nums);
        return result;
    }
    void backtrack(int startIndex, vector<int>& nums) {
        result.push_back(path);
        for (int i = startIndex; i < nums.size(); i++) {
            // 关键：同层去重
            if (i > startIndex && nums[i] == nums[i - 1]) continue;
            path.push_back(nums[i]);
            backtrack(i + 1, nums);
            path.pop_back();
        }
    }
private:
    vector<vector<int>> result;
    vector<int> path;
};

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        res, path = [], []
        def backtrack(start):
            res.append(path[:])
            for i in range(start, len(nums)):
                if i > start and nums[i] == nums[i-1]: # 同层去重
                    continue
                path.append(nums[i])
                backtrack(i + 1)
                path.pop()
        backtrack(0)
        return res

复杂度分析

• 时间复杂度：O(n * 2ⁿ)。
• 空间复杂度：O(n)。

128. 最长连续序列 (Longest Consecutive Sequence)

问题描述

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。要求算法的时间复杂度为 O(n)。

示例：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长连续序列是 [1, 2, 3, 4]。长度为 4。

解题思路

利用哈希集合（HashSet）实现 O(1) 时间复杂度的查找。

1. 将所有数字存入一个集合 num_set 中，实现去重和快速查找。
2. 遍历集合中的每个数字 num。关键：只有当 num-1 不在集合中时，才以 num 为起点开始向后（num+1, num+2...）寻找连续序列。这是因为如果 num-1 存在，那么 num 肯定不是某个连续序列的起点，计算它会导致重复。
3. 记录每个序列的长度，并更新最大值。

参考代码

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set(nums.begin(), nums.end());
        int res = 0;
        for (int num : num_set) {
            // 只有当num是序列起点时才计算
            if (!num_set.count(num - 1)) {
                int curNum = num;
                int curLen = 1;
                while (num_set.count(curNum + 1)) {
                    curNum++;
                    curLen++;
                }
                res = max(res, curLen);
            }
        }
        return res;
    }
};

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        num_set = set(nums)
        res = 0
        for num in num_set:
            if num - 1 not in num_set: # 是序列起点
                cur_num = num
                cur_len = 1
                while cur_num + 1 in num_set:
                    cur_num += 1
                    cur_len += 1
                res = max(res, cur_len)
        return res

复杂度分析

• 时间复杂度：O(n)。每个元素最多被访问两次（一次在集合中，一次在作为起点时扩展序列）。
• 空间复杂度：O(n)，用于存储哈希集合。

300. 最长递增子序列 (Longest Increasing Subsequence, LIS)

问题描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列不要求连续。

示例：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，长度为 4。

解题思路（动态规划）

定义 dp[i] 表示以 nums[i] 为结尾的最长递增子序列的长度。
状态转移方程：dp[i] = max(dp[j]) + 1，其中 0 <= j < i 且 nums[j] < nums[i]。
最终结果是 dp 数组中的最大值。

参考代码 (DP)

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 1);
        int res = 1;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (nums[i] > nums[j]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            res = max(res, dp[i]);
        }
        return res;
    }
};

解题思路（贪心 + 二分查找 - 更优）

维护一个数组 tail，tail[i] 表示长度为 i+1 的所有递增子序列中，结尾数字最小的那个结尾数字。可以证明 tail 是严格递增的。
遍历 nums：

• 如果 nums[i] 大于 tail 的最后一个元素，直接追加，序列长度+1。
• 否则，在 tail 中寻找第一个大于等于 nums[i] 的位置，将其替换为 nums[i]（使用二分查找）。这不会改变已有序列的长度，但让该长度的子序列的结尾数字变得更小，更有潜力接上后续的数字。

参考代码 (贪心+二分)

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> tail;
        for (int num : nums) {
            // 寻找第一个 >= num 的位置
            auto it = lower_bound(tail.begin(), tail.end(), num);
            if (it == tail.end()) {
                tail.push_back(num); // 比所有结尾都大，扩展序列
            } else {
                *it = num; // 替换，使该长度的结尾最小化
            }
        }
        return tail.size(); // tail的长度就是LIS的长度
    }
};

复杂度分析

• 动态规划：时间复杂度 O(n²)，空间复杂度 O(n)。
• 贪心+二分：时间复杂度 O(n log n)，空间复杂度 O(n)。这是更优的解法。

416. 分割等和子集 (Partition Equal Subset Sum)

问题描述

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

解题思路

转化为 0-1 背包问题。若数组总和为 sum，问题等价于：能否从数组中选出一些数，使得它们的和等于 target = sum / 2。
定义 dp[j] 为：是否存在一个子集，其元素和为 j。
状态转移：对于每个数字 num，dp[j] = dp[j] || dp[j - num]（需从后向前遍历，防止重复使用数字）。

参考代码

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = accumulate(nums.begin(), nums.end(), 0);
        if (sum % 2 != 0) return false;
        int target = sum / 2;
        vector<bool> dp(target + 1, false);
        dp[0] = true;
        for (int num : nums) {
            for (int j = target; j >= num; --j) { // 从后向前
                dp[j] = dp[j] || dp[j - num];
                if (dp[target]) return true; // 提前结束
            }
        }
        return dp[target];
    }
};

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total = sum(nums)
        if total % 2: return False
        target = total // 2
        dp = [True] + [False] * target
        for num in nums:
            for i in range(target, num - 1, -1): # 从后向前
                dp[i] = dp[i] or dp[i - num]
                if dp[target]: return True
        return dp[target]

复杂度分析

• 时间复杂度：O(n * target)，其中 target 为数组和的一半。
• 空间复杂度：O(target)。

LeetCode连续子数组问题精解

3. 无重复字符的最长子串 (Longest Substring Without Repeating Characters)

问题描述

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例：

输入: s = "abcabcbb"
输出: 3 
解释: 无重复字符的最长子串是 "abc"，长度为 3。

解题思路

经典的滑动窗口问题。

• 使用两个指针 left 和 right 表示当前窗口的左右边界，初始都为0。
• 用一个哈希集合 window_set 存储当前窗口内的字符。
• 不断移动 right 指针扩大窗口。如果 s[right] 已存在于 window_set 中，说明出现了重复，则不断移动 left 指针缩小窗口（并从集合中移除 s[left]），直到重复字符被移出窗口。
• 在每次扩大窗口后，更新最大长度。

参考代码

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_set<char> window_set;
        int left = 0, res = 0;
        for (int right = 0; right < s.size(); ++right) {
            while (window_set.count(s[right])) { // 出现重复，收缩左边界
                window_set.erase(s[left]);
                left++;
            }
            window_set.insert(s[right]);
            res = max(res, right - left + 1);
        }
        return res;
    }
};

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        window_set = set()
        left = res = 0
        for right, char in enumerate(s):
            while char in window_set:
                window_set.remove(s[left])
                left += 1
            window_set.add(char)
            res = max(res, right - left + 1)
        return res

复杂度分析

• 时间复杂度：O(n)，每个字符最多被 left 和 right 指针各访问一次。
• 空间复杂度：O(字符集大小)，哈希集合的开销。

53. 最大子数组和 (Maximum Subarray)

问题描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组，并返回其最大和。子数组至少包含一个元素。

示例：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6。

解题思路（动态规划）

定义 dp[i] 为以 nums[i] 结尾的连续子数组的最大和。
状态转移方程：dp[i] = max(dp[i-1] + nums[i], nums[i])。
因为 dp[i] 只与 dp[i-1] 有关，可以用一个变量 pre 来压缩空间。

参考代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int pre = 0, res = nums[0];
        for (int num : nums) {
            pre = max(pre + num, num); // 要么接上前面，要么自己另起炉灶
            res = max(res, pre);
        }
        return res;
    }
};

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        pre, res = 0, nums[0]
        for num in nums:
            pre = max(num, pre + num)
            res = max(res, pre)
        return res

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。

152. 乘积最大子数组 (Maximum Product Subarray)

问题描述

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组，并返回该子数组的乘积。

示例：

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

解题思路

由于存在负数，乘积的最大值可能由当前的最大值乘负数（得到新的最小值），或最小值乘负数（得到新的最大值）而来。因此需要同时维护以当前元素结尾的最大乘积 max_f 和最小乘积 min_f。
状态转移：

• temp_max = max_f
• max_f = max(nums[i], max_f * nums[i], min_f * nums[i])
• min_f = min(nums[i], temp_max * nums[i], min_f * nums[i])

参考代码

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int max_f = nums[0], min_f = nums[0], res = nums[0];
        for (int i = 1; i < nums.size(); ++i) {
            int mx = max_f, mn = min_f; // 保存旧值
            max_f = max({nums[i], mx * nums[i], mn * nums[i]});
            min_f = min({nums[i], mx * nums[i], mn * nums[i]});
            res = max(res, max_f);
        }
        return res;
    }
};

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        max_f = min_f = res = nums[0]
        for i in range(1, len(nums)):
            mx, mn = max_f, min_f
            max_f = max(nums[i], mx * nums[i], mn * nums[i])
            min_f = min(nums[i], mx * nums[i], mn * nums[i])
            res = max(res, max_f)
        return res

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。

560. 和为K的子数组 (Subarray Sum Equals K)

问题描述

给定一个整数数组 nums 和一个整数 k ，请统计并返回该数组中和为 k 的连续子数组的个数。

示例：

输入：nums = [1,1,1], k = 2
输出：2

解题思路

前缀和 + 哈希表。定义 pre[i] 为 nums[0..i] 的和。则子数组 nums[j..i] 的和为 pre[i] - pre[j-1]。
问题转化为：对于每个 i，有多少个 j (j < i) 满足 pre[j] = pre[i] - k。
我们可以在遍历数组计算前缀和的同时，用一个哈希表 prefix_map 记录每个前缀和出现的次数。对于当前前缀和 pre，res += prefix_map[pre - k]，然后更新 prefix_map[pre]。

参考代码

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> prefix_map;
        prefix_map[0] = 1; // 前缀和为0出现一次
        int pre = 0, res = 0;
        for (int num : nums) {
            pre += num;
            if (prefix_map.count(pre - k)) {
                res += prefix_map[pre - k];
            }
            prefix_map[pre]++;
        }
        return res;
    }
};

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        from collections import defaultdict
        prefix_map = defaultdict(int)
        prefix_map[0] = 1
        pre = res = 0
        for num in nums:
            pre += num
            res += prefix_map[pre - k]
            prefix_map[pre] += 1
        return res

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(n)，哈希表开销。

581. 最短无序连续子数组 (Shortest Unsorted Continuous Subarray)

问题描述

给你一个整数数组 nums ，你需要找出一个连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。请你找出符合题意的最短子数组，并输出它的长度。

示例：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：只需要对 [6, 4, 8, 10, 9] 排序，整个数组就会有序。

解题思路

数组可以分成三部分：numsA, numsB, numsC。numsB 是乱序部分，排序后整个数组有序。那么 numsA 的所有元素都小于 numsB 和 numsC 中的任意元素，numsC 的所有元素都大于 numsB 和 numsA 中的任意元素。

我们可以：

1. 从左到右遍历，找到最后一个位置 right，其值小于左边遍历过的最大值。
2. 从右到左遍历，找到最后一个位置 left，其值大于右边遍历过的最小值。
   那么 [left, right] 就是需要排序的最短子数组。

参考代码

class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        int n = nums.size();
        int maxn = INT_MIN, right = -1;
        int minn = INT_MAX, left = -1;
        for (int i = 0; i < n; ++i) {
            // 从左到右，找右边界
            if (maxn > nums[i]) {
                right = i; // 当前元素比左边最大值小，说明它位置不对
            } else {
                maxn = nums[i];
            }
            // 从右到左，找左边界
            int j = n - 1 - i;
            if (minn < nums[j]) {
                left = j; // 当前元素比右边最小值大，说明它位置不对
            } else {
                minn = nums[j];
            }
        }
        return right == -1 ? 0 : right - left + 1;
    }
};

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。

718. 最长重复子数组 (最长公共子数组)

问题描述

给两个整数数组 nums1 和 nums2 ，返回两个数组中公共的、长度最长的子数组的长度。

示例：

输入：
nums1: [1,2,3,2,1]
nums2: [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3, 2, 1]。

解题思路（动态规划）

定义 dp[i][j] 为以 nums1[i-1] 和 nums2[j-1] 为结尾的最长公共子数组的长度（这样定义可以方便处理边界）。
状态转移：
如果 nums1[i-1] == nums2[j-1]，则 dp[i][j] = dp[i-1][j-1] + 1。
否则，dp[i][j] = 0（因为是连续子数组，一旦不等就断开）。
在计算过程中记录 dp[i][j] 的最大值。

参考代码

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        int res = 0;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    res = max(res, dp[i][j]);
                } // else dp[i][j] = 0
            }
        }
        return res;
    }
};

复杂度分析

• 时间复杂度：O(m * n)。
• 空间复杂度：O(m * n)。可以用滚动数组优化到 O(min(m, n))。

总结

数组子数组问题涵盖了算法面试中的大量高频考点。关键在于准确识别问题是关于连续子数组还是不连续子数组，从而选择正确的解题框架：滑动窗口/前缀和/DP 或 回溯/DP。通过本文对多个经典题目的解析，希望读者能建立起清晰的解题思路，在遇到类似问题时能够快速应对。