卡诺图化简法与逻辑代数：数字电路设计中的逻辑函数化简实战指南

本文详细介绍了组合逻辑电路设计中的两种核心化简方法：卡诺图化简法和逻辑代数化简法。内容涵盖卡诺图的绘制与化简规则、逻辑代数的基本定律与原则，并通过大量实例解析函数化简过程。最后，探讨了数字电路中竞争与冒险现象的产生原因及消除方法，适合电子工程、计算机科学及数字逻辑领域的学习者与工程师参考。

一、卡诺图化简法

卡诺图是一种利用图形化方法对逻辑函数进行化简的强大工具，特别适合处理变量数较少的情况。

1. 前置知识：最小项

在深入卡诺图之前，必须理解最小项的概念。

• 最小项的定义：一个包含了函数所有变量的乘积项，其中每个变量都以原变量或反变量的形式出现且仅出现一次。
• 最小项的表示方法：通常用 $m_i$ 表示。下标 i 的确定方法是：将最小项中的原变量记为 1，反变量记为 0，形成一个二进制数，其对应的十进制数即为下标 i。

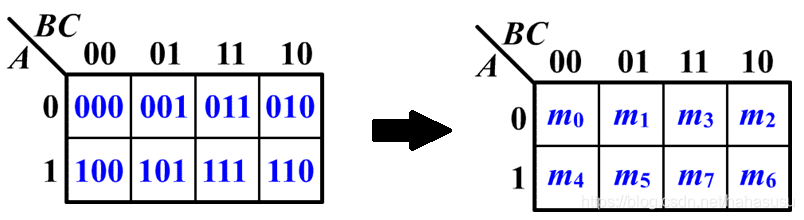
例如，对于三变量函数 L(A, B, C)：

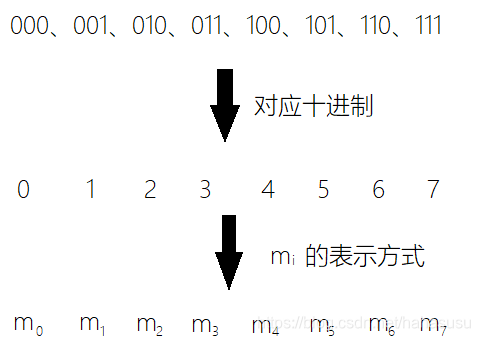
由此可以确定各个最小项：

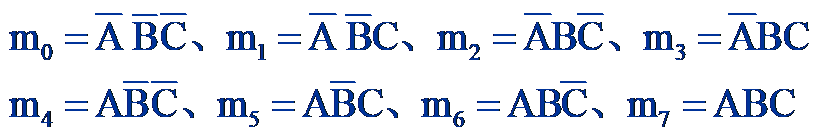
• 最小项的相邻性：如果两个最小项只有一个因子不同，其余因子完全相同，则称它们为相邻最小项。例如，$m_0$ 和 $m_1$ 相邻。相邻的最小项可以合并并消去一个变量。

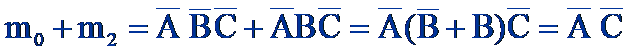
2. 卡诺图的构造与特点

卡诺图是一种特殊的方格图，由美国工程师卡诺（Karnaugh）提出，其核心特点是几何位置相邻的方格，所代表的最小项在逻辑上也相邻。

• 对于 n 个变量的逻辑函数，其卡诺图由 $2^n$ 个方格构成，每个方格对应一个最小项。
• 变量排列遵循格雷码顺序，确保相邻性。

两变量卡诺图：

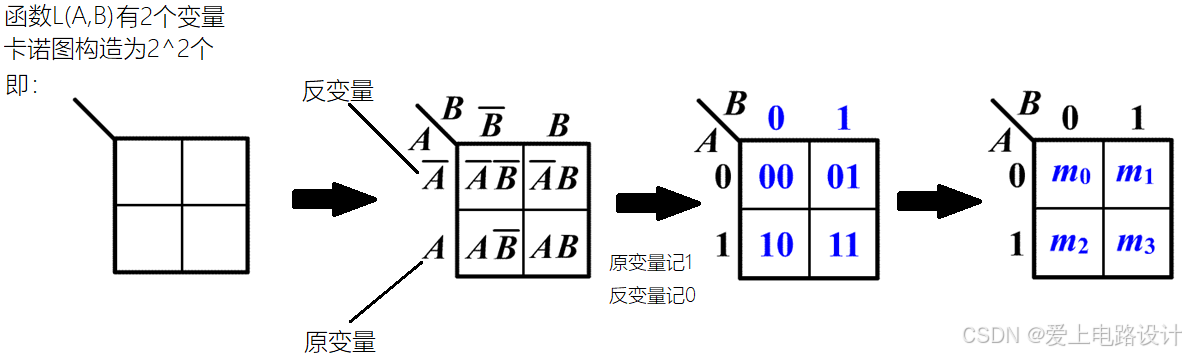
三变量卡诺图：

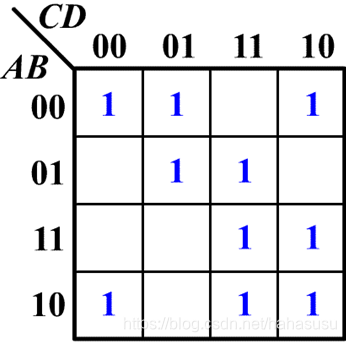
示例：画出逻辑函数 $F(A,B,C,D) = \sum m(0,1,2,5,7,8,10,11,14,15)$ 的卡诺图。
解：在四变量卡诺图中，将序号为 0,1,2,5,7,8,10,11,14,15 的方格填入 1，其余填入 0。

3. 卡诺图化简法

利用卡诺图中相邻项可合并的特性进行化简，基本原则是画圈合并。

• 化简规则：
  1. 两个相邻 1 格可合并为一项，消去一个变量。
  2. 四个相邻 1 格可合并为一项，消去两个变量。
  3. 八个相邻 1 格可合并为一项，消去三个变量。
     （以此类推，合并的方格数必须为 2 的幂次）

示例：两个相邻项的合并

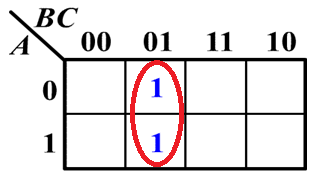化简得：$m_1 + m_5 = BC$

示例：四个相邻项的合并

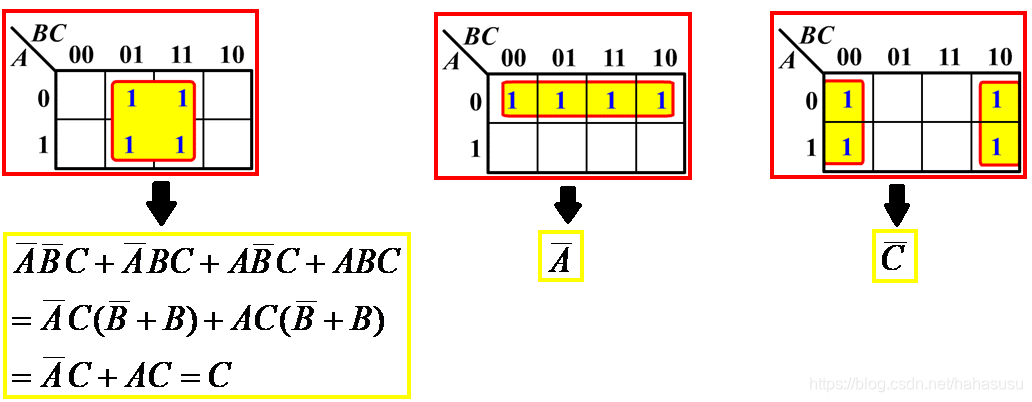化简得：$m_1+m_3+m_5+m_7 = C$

画圈合并的具体步骤与原则：

1. 填图：将函数转化为最小项表达式，并填入卡诺图。
2. 画圈：对图中的 1 格进行画圈合并。需遵循：
   • 圈尽所有1：每个 1 格至少被一个圈覆盖。
   • 圈大优先：在满足前一条的前提下，圈越大越好（消去变量多）。
   • 圈数最少：圈的个数越少越好（与项少）。
   • 独立新1：每个圈应至少包含一个未被其他圈覆盖过的 1 格，避免冗余。

画圈正误对比示例：

• 错误（多画圈） vs 正确：
  
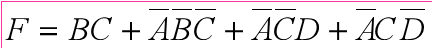
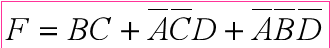
• 错误（圈不够大） vs 正确：
  
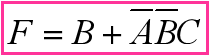
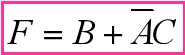
• 错误（圈内无新1格）：
  

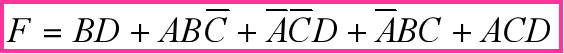
4. 包含无关项的卡诺图化简

在实际的数字系统或网络/系统设计中，某些输入组合永远不会出现，或对输出没有影响，这些项称为无关项（Don‘t Care Terms）。在卡诺图中用 × 表示。

• 化简技巧：充分利用无关项 × 的灵活性，可根据需要将其看作 1 或 0，以帮助画更大的圈，获得更简化的表达式。

示例：已知 $F(A,B,C,D) = \sum m(1,2,3,6,7) + \sum d(10,11,12,13,14,15)$，求最简与或式。
解：填图时，最小项填1，无关项填×。画圈时，将有助于扩大圈的×视为1。

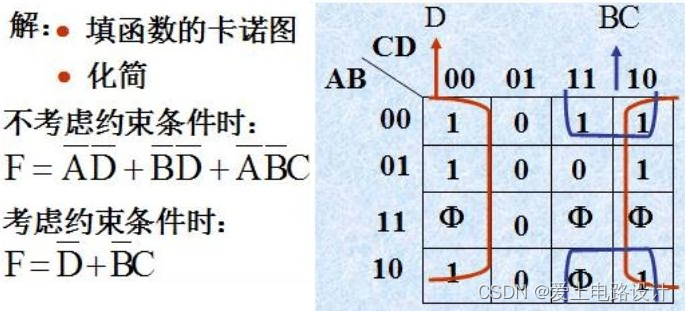化简结果为：$F = \bar{B} + AC$

5. 手动化简总结与软件工具

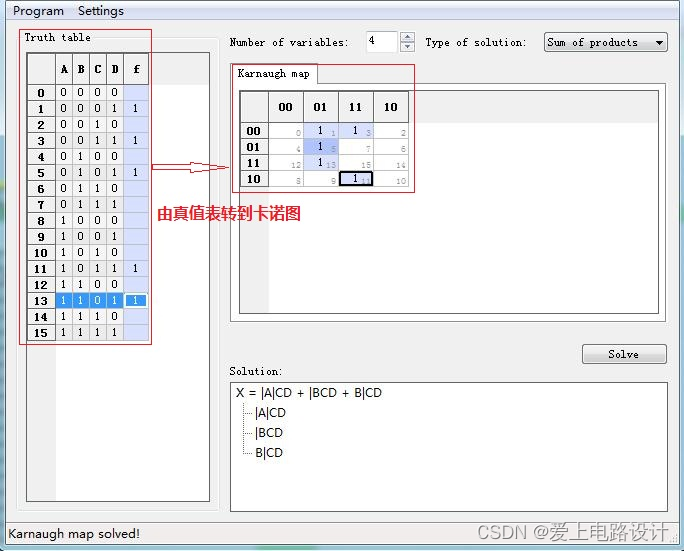
• 总结：卡诺图法直观简单，但通常适用于变量数 ≤ 5 的情况。变量过多时，图形过于复杂，可借助算法/数据结构思想或软件工具辅助。
• 软件工具：可使用专门的逻辑函数化简软件（如 K-map minimizer）。基本流程是输入真值表或最小项表达式，软件自动生成化简结果。
  

二、逻辑代数化简法

逻辑代数化简法（公式法）运用布尔代数的基本定律和规则进行推导化简，适用于各种复杂函数，但要求熟练运用公式。

1. 逻辑代数的基本定律

以下定律成对出现，互为对偶式。

• 0-1律、交换律、结合律：
  
  

• 分配律、互补律、重叠律、还原律：
  

• 反演律（摩根定理）、吸收律：
  
  

• 冗余定律（多余项定理）：
  
  推论：$AB + \bar{A}C + BC = AB + \bar{A}C$

2. 逻辑代数的三个基本原则

1. 代入规则：等式中的任一变量都可用另一个函数替代，等式依然成立。
2. 对偶规则：将函数式 $F$ 中所有的 · 与 + 互换，0 与 1 互换，变量保持不变，得到的新式子 $F‘$ 称为 $F$ 的对偶式。
3. 反演规则：求函数 $F$ 的反函数 $\bar{F}$ 时，将 $F$ 中所有的 · 与 + 互换，0 与 1 互换，原变量与反变量互换，并保持原运算顺序。

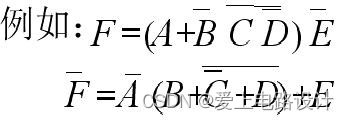
3. 逻辑函数式的化简

代数化简的目标是得到最简与或式：与项个数最少，且每个与项内的变量数最少。

常用化简技巧：

• 并项法：利用 $AB + A\bar{B} = A$
• 吸收法：利用 $A + AB = A$ 或 $A + \bar{A}B = A + B$
• 消去法：利用 $AB + \bar{A}C + BC = AB + \bar{A}C$
• 配项法：乘以 $(A+\bar{A})$ 增加项，以便与其他项合并化简。

化简示例：
$F = A\bar{B} + \bar{A}B + B\bar{C} + \bar{B}C$
$= A\bar{B} + \bar{A}B(C+\bar{C}) + B\bar{C} + \bar{B}C(A+\bar{A})$ （配项）
$= A\bar{B} + \bar{A}BC + \bar{A}B\bar{C} + B\bar{C} + A\bar{B}C + \bar{A}\bar{B}C$
$= A\bar{B}(1+C) + B\bar{C}(1+\bar{A}) + \bar{A}C(B+\bar{B})$
$= A\bar{B} + B\bar{C} + \bar{A}C$

三、竞争与冒险

在组合逻辑电路中，信号经过不同路径产生的延迟可能导致瞬时错误输出，这种现象称为冒险。

1. 产生原因

当某个输入变量通过两条或以上路径到达输出端，且各路延迟时间不同时，就会产生“竞争”。若竞争导致输出出现不应有的尖峰脉冲（毛刺），则称为“冒险”。

2. 类型与判断

• “0”型冒险：输出产生负向尖脉冲。表现为化简后函数在特定条件下出现 $F = A + \bar{A}$ 的形式。
• “1”型冒险：输出产生正向尖脉冲。表现为化简后函数在特定条件下出现 $F = A · \bar{A}$ 的形式。

判断方法：检查函数中每个具有竞争条件的变量（以原、反变量形式出现），令其他变量为特定值（0或1），看函数是否能化为 $A+\bar{A}$ 或 $A·\bar{A}$ 的形式。

示例：判断 $F = AC + \bar{A}B + \bar{A}\bar{C}$ 是否存在冒险。

• 考虑变量A：令 B=1， C=0，则 $F = A·0 + \bar{A}·1 + \bar{A}·1 = \bar{A}$，不会出现 $A+\bar{A}$。令 B=0， C=1，则 $F = A·1 + \bar{A}·0 + \bar{A}·0 = A$，也不会。但，令 B=1， C=1，则 $F = A·1 + \bar{A}·1 + \bar{A}·0 = A + \bar{A}$，存在“0”型冒险。
• 考虑变量B和C：它们不具备竞争条件（未同时以原、反变量出现）。

3. 消除方法

1. 修改逻辑设计：增加冗余项。例如对上例，增加冗余项 $BC$，则 $F = AC + \bar{A}B + \bar{A}\bar{C} + BC$。当 B=1，C=1时，$BC=1$，封锁了 $A+\bar{A}$ 产生的毛刺。
2. 输出端接滤波电容：在输出端并联一个几十到几百皮法（pF）的小电容，可以滤除高频的窄脉冲毛刺。
3. 引入选通脉冲：在电路输出稳定后，才让选通脉冲有效，读取输出值。