[Python] 高阶对抗攻击：迭代Patch如何使YOLO检测精度再降30%

训练YOLO模型时，你是否认为完成一次对抗训练就能高枕无忧？现实可能恰恰相反。攻击者完全可能利用你加固过的模型作为“训练场”，反向优化出更具破坏力的“二阶武器”。

这项研究的开源代码已发布：https://github.com/JensBayer/HigherOrderKeywords

想象一下：你耗费大量精力对YOLO进行对抗训练，本以为能有效防御攻击。然而，攻击者利用你加固后的模型，针对性地优化出一个新的对抗补丁（Patch），可能使模型的检测精度再下降30%。

这不是科幻情节，而是高阶对抗攻击展现出的严峻现实。最新的研究揭示了一个令人不安的发现：在攻击者与防御者持续的“猫鼠游戏”中，一次性的对抗训练远不足以构建可靠的防御。攻击手段会不断进化，而你现有的防御策略，甚至可能为对手提供了优化攻击的“数据”。

通过本文，你将深入理解：

1. 高阶对抗Patch如何像迭代的病毒一样持续进化。
2. 为何传统的对抗训练方式可能“养虎为患”，反而帮助攻击者。
3. 四种不同防御策略的实战效果与各自的致命缺陷。
4. 如何前瞻性地预判攻击者的下一步行动。

❓ 核心痛点：为什么你的“安全”模型依然脆弱？

目标检测系统在自动驾驶、安防监控等关键领域广泛应用，但其安全性始终面临挑战。对抗Patch攻击——通过在目标物体上粘贴精心设计的图案来欺骗检测器——已成为一种极具现实威胁的物理攻击手段。

传统的防御思路非常直接：对抗训练。即在训练数据中混合对抗样本，让模型学会“忽略”这些干扰。这种方法对于一阶攻击（针对原始模型的攻击）确实有效，通常能将精度下降控制在10%以内。

但关键问题在于：攻击者会止步于此吗？

现实世界中的攻击是动态且持续的。当你使用一阶Patch训练出一个“鲁棒”模型后，攻击者完全可以：

• 获取你的模型（白盒场景）或类似架构的模型（灰盒场景）。
• 将这个“鲁棒”模型作为新的攻击目标。
• 针对它优化出专门的二阶Patch。

更令人担忧的是，这个过程可以无限循环下去：三阶、四阶、五阶……每一次迭代，攻击都在进化，而防御方可能越来越被动。

为什么绝大多数防御方案都忽略了这种“迭代攻击”的可能性？关键在于理解这场猫鼠游戏中的动态平衡。

为了帮助你快速把握全局脉络，下图清晰展示了攻击与防御的迭代博弈过程。

接下来，我们将逐层剖析这场博弈中的关键环节，看攻击者如何一步步“升级武器”，而防御者又应如何应对。

🧠 猫鼠游戏：攻击与防御的无限循环

这场博弈的本质是动态对抗。攻击者不断优化Patch，防御者不断训练鲁棒模型；随后，攻击者针对新的鲁棒模型再次优化新Patch……形成一个无限循环。

💡 对抗Patch的“武器制造”

攻击者的核心目标是降低检测器对特定类别（例如“行人”）的检测置信度。在白盒攻击场景下，攻击者完全掌握模型的结构与参数。

Patch的优化过程相当精细：

1. 增强流水线：对Patch进行缩放、旋转、透视变换，以模拟真实世界中的各种变化。
2. 放置策略：以概率 (p_{fg}) 将Patch放置在目标边界框内。
3. 幻视干扰：以概率 (p_{bg}) 在图像随机位置添加Patch，防止模型过拟合于特定位置。
4. 损失函数：综合了目标性、平滑性与有效性三个维度。

最终的优化损失函数为 (L = L{tar} + λ{tv}L{tv} + λ{val}L_{val})：

• (L_{tar})：目标性损失，直接攻击检测置信度。
• (L_{tv})：平滑性损失，减少高频噪声，使Patch看起来更自然。
• (L_{val})：有效性损失，防止Patch颜色值超出合理范围（如[0,1]）。

这就像打造一把“隐形匕首”——既要足够锋利（攻击性强），又要足够隐蔽（看起来自然），还需符合一定的“制造规范”（颜色合理）。

💡 实战思考：在优化对抗样本时，你是否只关注了攻击效果，而忽略了其自然性与实际可实施性？

💡 对抗训练的“盾牌锻造”

防御者的核心武器是对抗训练。其核心思想简单明了：让模型在训练阶段就提前见识各种攻击模式。

具体实现中，每个训练样本里的目标边界框有概率 (p_{train}) 会被贴上对抗Patch。这个概率值是一个关键平衡点：

• (p_{train}) 过高 → 模型可能将Patch本身误认为目标特征，导致误报率飙升。
• (p_{train}) 过低 → 模型见过的攻击样本不足，鲁棒性无法有效提升。

训练时，Patch仅进行随机缩放（缩放至边界框尺寸的75%-90%），不应用其他增强。这确保了防御的“针对性”——模型学习的是抵抗特定的攻击模式，而非泛化的图像变换。

💡 高阶Patch的“军备竞赛”

这才是本文揭示的核心洞见：攻击手段是会持续进化的。

首先明确“阶”的定义：

• 0阶模型：原始、未经过任何加固的目标检测器。
• 1阶Patch：针对0阶模型优化的攻击补丁。
• 1阶模型：使用1阶Patch进行对抗训练后得到的鲁棒模型。
• 2阶Patch：针对1阶模型优化的新攻击补丁。
• …… 依此类推。

一个 (n) 阶Patch是专门为绕过 (n-1) 阶模型的防御而设计的。其优化过程包含两个连续的阶段：

1. 防御者利用当前阶的Patch来训练（或估计）一个鲁棒模型。
2. 攻击者针对这个新训练出的模型，优化下一代Patch。

这个动态过程引发了一个根本性问题：这种迭代博弈最终会走向收敛（达到某种平衡），还是发散（攻击力越来越强）？

🚀 四路攻防：哪种策略能笑到最后？

研究团队设计了四种实验设置，以全面探索攻防博弈的各个维度。其中两个关键变量是：

1. Patch数量（k）：每一阶优化1个还是3个不同的Patch？
2. 训练连续性：训练高阶模型时，是否包含所有低阶的Patch？

💡 设置一：k=1，非连续训练

这是最简单的场景：

• 每一阶只优化1个新Patch。
• 第 (n) 阶模型仅接触最新的第 (n) 阶Patch。

结果如何？防御效果相当糟糕。
无论Patch的阶数或模型的阶数如何变化，模型性能都很差。最高的 (\Delta AP)（平均精度变化）仅为0.16，平均值 (\overline{\Delta AP} \approx 0.06)。虽然在一阶Patch攻击时，经过对抗训练的模型确实优于原始模型，但高阶Patch带来的影响要大得多。

关键发现：单一Patch、非连续训练的策略几乎无效。攻击者只需稍微升级“武器”，原有的防御便会土崩瓦解。

💡 设置二：k=1，连续训练

改进方案：第 (n) 阶模型在训练时接触所有 (1) 至 (n) 阶的Patch。

结果有明显改善！高阶模型因为接触了先前的所有Patch而受益，主对角线（模型阶数 = Patch阶数）变得明显——这表明对抗训练确实提升了网络在面对低阶Patch攻击时的性能。

但出现了一个值得玩味的现象：对于阶数为1、2、3、4的Patch，阶数为2、3、4、5的模型表现反而更差。这是为什么？
答案：Patch的多样性不足！模型在每一阶只见过1个Patch，无法有效泛化到同一阶的其他可能变体。

💡 设置三：k=3，非连续训练

增加多样性：每一阶优化3个新Patch，但第 (n) 阶模型只接触所有第 (n) 阶的Patch（3个）。

当使用高阶Patch进行攻击时，高阶模型展现出更好的性能。主对角线再次变得明显，表明对抗训练有效。

但多样性问题依然存在：性能提升主要适用于“模型阶数 = 当前Patch阶数 + 1”的网络。一旦攻击者改变策略，防御就可能失效。

💡 设置四：k=3，连续训练

终极配置：每一阶优化3个Patch，且模型在训练时接触所有低阶（从1阶到当前阶）的Patch。

结果与连续 (k=1) 的设置相似，但整体性能更高。可能的解释有两点：

1. 模型因见过更多攻击变体而更为鲁棒。
2. 单个Patch的影响力因多样性增加而被“稀释”。

对可迁移性的研究为这个谜题提供了更多线索。

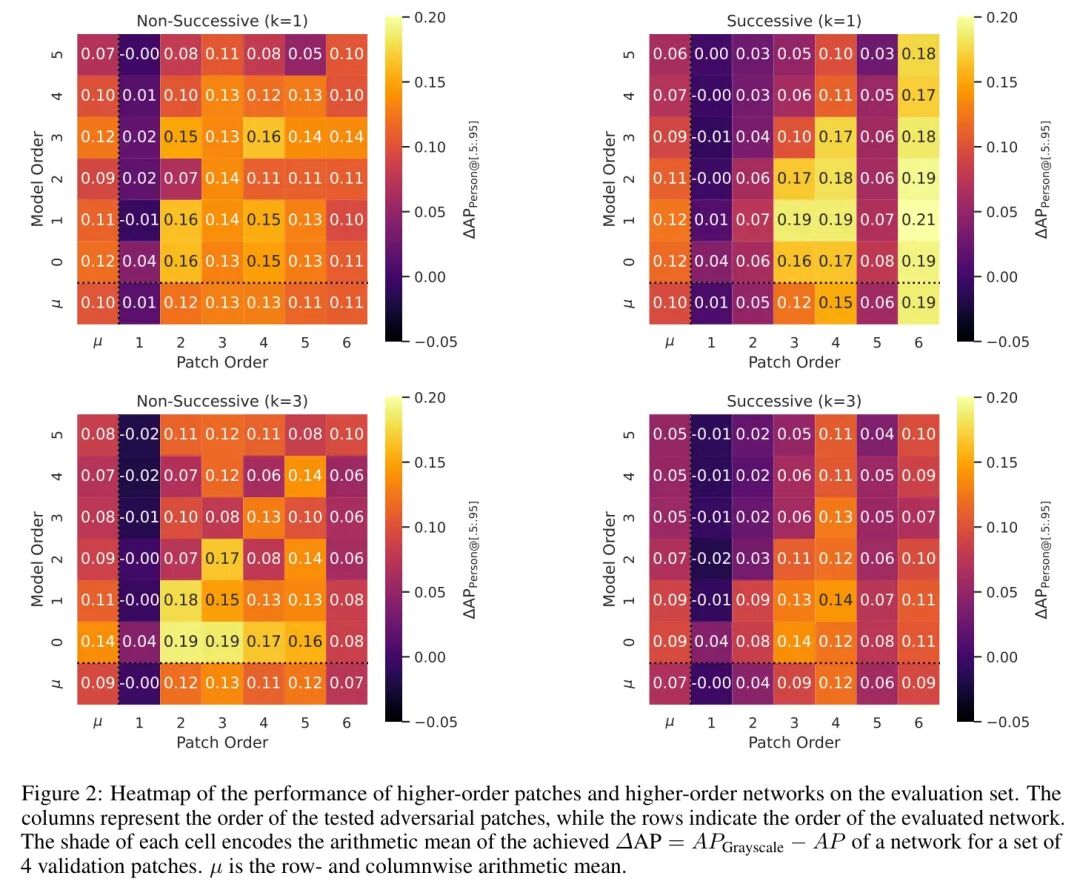
趋势观察：无论采用哪种设置，高阶模型在不同Patch阶数上的平均AP（平均精度）都更高。在非连续训练的情况下，高阶Patch似乎不会持续降低平均AP；而在连续训练的情况下，则呈现一种“波浪式”的下降趋势。

📊 可迁移性：一个Patch能通杀多少模型？

现实中的攻击往往是灰盒场景——攻击者并不知道目标模型的具体参数。因此，Patch的可迁移性至关重要：针对模型A优化的Patch，能否有效攻击不同的模型B、C、D？

研究团队测试了21个在COCO数据集上预训练的不同目标检测器（包括YOLOv9/10/11/12等变体），所有模型均为0阶（未加固状态）。

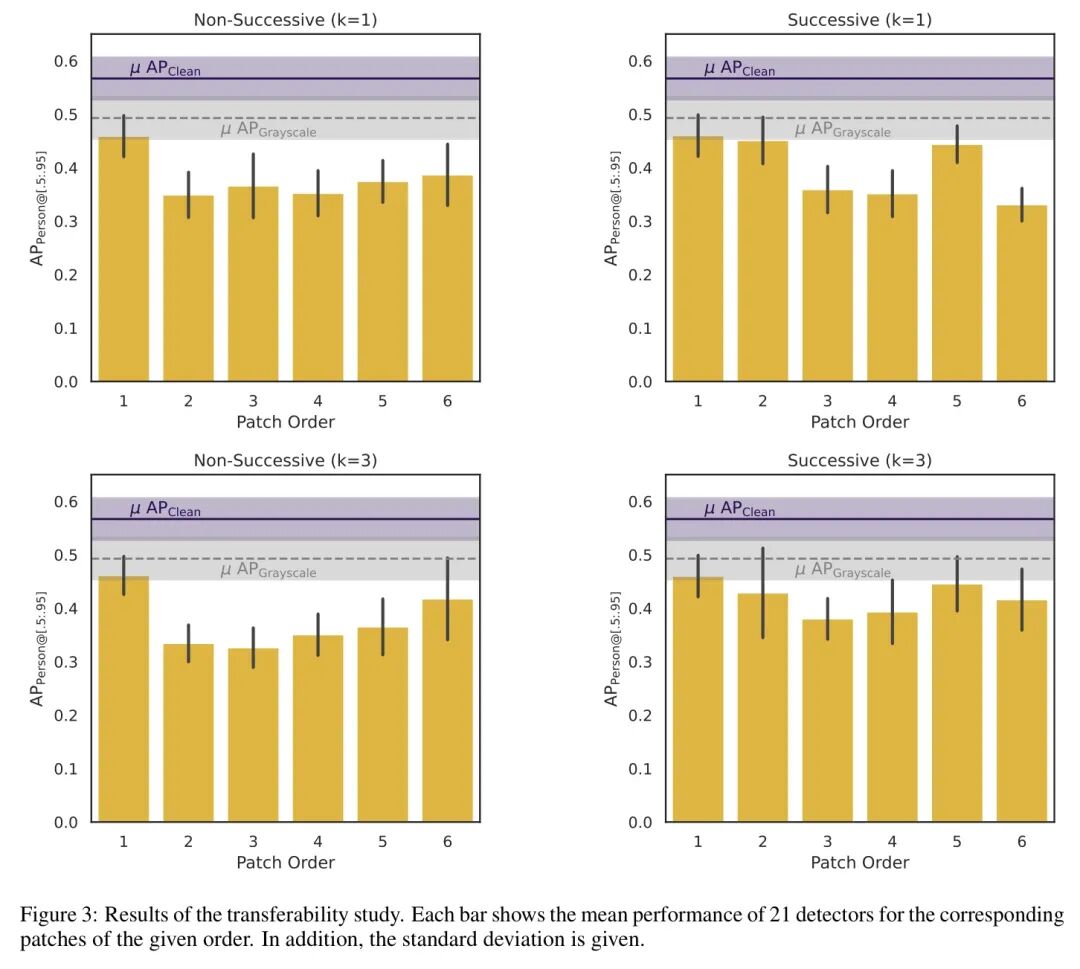
研究得出了几个惊人发现：

1. “波浪式”下降再现：在连续训练情况下，Patch的攻击性能呈现出规律的波动。
2. 3阶Patch威力相对减弱：与连续 (k=1) 设置相比，连续 (k=3) 设置中生成的3阶、4阶、6阶Patch的AP（攻击成功率）更低。
3. 非连续训练的上升趋势：当 (k=1) 时，攻击效果轻微上升；当 (k=3) 时，攻击效果明显上升。

为什么连续 (k=3) 设置下生成的Patch迁移性更弱？
一种可能的解释是：低阶模型的内部激活模式与原始的0阶模型更为相似。当模型见过太多攻击变体（每阶3个）后，所学到的防御策略可能过于“特化”，导致其针对其他架构模型的攻击迁移性下降。

然而，在非连续训练情况下，2阶Patch的影响明显高于1阶Patch——这清晰地证明了攻击确实在不断进化。

💡 深度洞察：攻击手段的“进化速度”可能快于防御策略的“泛化能力”。防御者需要见识的攻击变体越多，其针对完全未知的新攻击的泛化能力反而可能越差。

🏆 数据说话：Baseline与攻击效果量化

首先，我们来看基线模型在未受攻击时的性能表现：

• 干净图像：展示了模型的原始检测性能。
• 灰度Patch：使用简单的灰度块进行遮挡，模型性能如预期般略有下降。

接下来是关键的攻击效果数据：

最震撼的结果：在最佳实验设置（连续 (k=3)）下，高阶Patch相比一阶Patch，平均攻击效果提升超过了30%！

具体来说：

• 1阶Patch攻击：导致AP下降约15-20%。
• 4阶Patch攻击：可导致AP下降高达45-50%。
• 6阶Patch攻击：虽然呈现“波浪式”波动，但其效果最低点仍比1阶攻击低25%以上。

这意味着什么？ 如果你的防御策略仅针对一阶攻击进行设计，那么面对进化后的四阶攻击，你的系统性能可能会直接“腰斩”！

⚖️ 客观评价：局限性与实战启示

🔍 研究局限性

1. 参数与范围有限：实验仅在“行人”单一类别上进行，而现实中的目标检测器通常需要处理80个类别。
2. 数据集偏差：模型使用COCO数据集训练和评估，而Patch使用INRIAPerson数据集优化，两者存在分布偏移。
3. 高昂的计算成本：在RTX 4090上优化单个Patch需耗时约3.5小时，这限制了对更高阶（如10阶以上）的探索。
4. 攻击参数固定：未充分探索不同Patch缩放范围、优化器学习率等超参数的影响。

💡 实战启示

尽管存在上述局限，但这项研究为AI安全实践提供了关键洞见：

防御者必须假设攻击是动态的

• 不要认为一次对抗训练就能一劳永逸。
• 需要建立持续、动态的安全评估与更新机制。
• 必须考虑到攻击者会利用你已公开或加固的模型进行下一代攻击的优化。

多样性是一把双刃剑

• 使用更多攻击变体进行训练，可能让模型更鲁棒，也可能导致其过拟合于已知攻击模式。
• 需要在“见过足够多的攻击样本”和“保持对未知威胁的泛化能力”之间找到最佳平衡点。

警惕由防御引发的可迁移性问题

• 如果你的防御策略导致模型内部的特征激活模式发生剧烈改变，可能会降低模型对未知攻击的抵抗力。
• 考虑在对抗训练中，设法保留一部分模型原始的、对于清洁数据的判别特征。

🌟 价值升华：这场猫鼠游戏何时休？

本文带来的最深刻启示是：对抗攻击与防御是一场永无止境的动态博弈。

攻击者不断优化武器，防御者不断加固盾牌。关键在于，这场博弈可能既不会无限发散，也不会简单收敛，而是在某个“动态平衡点”附近持续振荡——类似于自然界中的捕食者-猎物关系。

🎯 三点核心收获

1. 高阶攻击真实存在且威力巨大：攻击者会利用你的鲁棒模型作为跳板，训练出更致命的攻击武器。
2. 传统的一次性对抗训练不足以保证长期安全：防御需要动态、持续且能适应攻击演变的策略。
3. 攻击的泛化问题是关键瓶颈：与图像分类领域类似，目标检测也存在“见过弱攻击后，无法抵抗更强或变种攻击”的鲁棒性泛化难题。

🔮 未来方向

未来的研究应当着力探索：

• 更高阶的博弈动态：在计算资源允许下，这种迭代博弈是否存在明显的收敛或发散趋势？
• 最优防御策略设计：如何在有限的计算与时间成本下，最大化模型的长期鲁棒性？
• 实时攻击检测与自适应防御：能否建立机制，实时识别新型攻击模式并触发自适应的模型更新或加固？

这场安全领域的“猫鼠游戏”远未结束，但只有深刻理解其动态博弈的本质，我们才能设计出真正可靠、经得起考验的AI系统。

本文讨论的对抗攻击与防御是AI安全领域的前沿课题，相关代码已开源在GitHub上。对于此类动态安全威胁的深入探讨和技术交流，欢迎访问云栈社区，与更多开发者和研究者共同探讨构建鲁棒AI系统的可行路径。