非参数方法估算期权希腊字母：机器学习在风险管理中的应用

传统期权定价依赖Black-Scholes模型计算Greeks进行风险对冲，但该模型的核心假设——对数正态分布与恒定波动率——与市场现实严重脱节。本文提出了一种基于机器学习的非参数Greeks估计框架，利用累积局部效应（Accumulated Local Effects, ALEs）从市场数据中直接提取期权敏感性指标。研究发现：市场隐含的Vega在高波动率区间趋于饱和，Gamma在平值附近呈现更尖锐的峰值，Theta衰减呈现非线性模式——这些发现揭示了传统模型在捕捉真实市场风险敞口方面的重大局限性，为量化交易者提供了一种更贴近市场实际的风险度量工具。

背景与现象

自Black and Scholes (1973)开创性工作以来，期权定价理论已发展近半个世纪。尽管Black-Scholes模型因其解析形式的Greeks而在实务中广泛应用，但其底层假设——标的资产价格服从对数正态分布、波动率恒定——与市场经验证据存在根本性矛盾。

实证研究表明，真实市场收益率分布呈现显著的尖峰厚尾特征，极端事件发生频率远高于正态分布预测。论文展示的S&P 500日收益率分布与高斯分布的对比清晰表明：实际分布在均值附近更为集中，尾部更为肥厚，符合Mandelbrot (1963)所描述的Pareto-Lévy稳定分布特征。

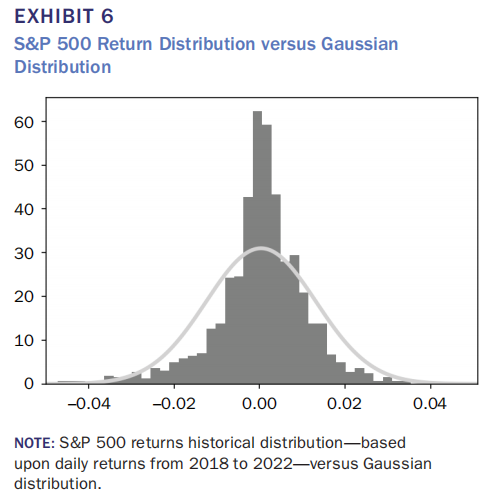
Exhibit 6 说明S&P 500实际收益率分布与高斯分布的显著差异，揭示Black-Scholes模型分布假设的失效。

这一分布偏差直接导致了两个核心问题：

1. 定价偏差：Black-Scholes模型系统性地高估期权价格，特别是在高波动率和长期限情景下；
2. Greeks失真：基于错误分布假设计算的敏感性指标无法准确反映市场隐含的风险敞口。

传统上，量化研究者尝试通过引入随机波动率模型（如Heston模型）或跳跃扩散模型来修正这些偏差。然而，这些方法仍需指定特定的数据生成过程，无法完全摆脱参数假设的约束。本文另辟蹊径，采用机器学习方法直接从市场数据中学习定价函数，并利用可解释性技术提取市场隐含的Greeks。

核心逻辑

方法论创新：从ALE到Greeks

本文的核心技术贡献在于将累积局部效应（ALE）——一种用于解释黑箱模型的可视化工具——重新定位为Greeks的计算基础。

与传统的部分依赖图（Partial Dependence Plots）不同，ALE方法能够正确处理特征之间的相关性问题。在期权数据中，波动率与到期时间等变量往往高度相关，ALE通过计算条件于实际数据分布的边际效应，避免了外推到不现实的特征组合区域。

ALE的计算过程如下：首先将特征 (x_j) 的取值范围划分为 (K) 个等频分箱，然后计算每个分箱内模型预测值的平均变化量：

[\hat{f}{j, ALE}(x) = \sum{k=1}^{k_j(x)} \frac{1}{nj(k)} \sum{i: x_{j}^{(i)} \in Nj(k)} \left[ f(z{k,j}, x{-j}^{(i)}) - f(z{k-1,j}, x_{-j}^{(i)}) \right]]

其中 (z_{k,j}) 为分箱边界，(N_j(k)) 为落入第 (k) 个分箱的观测索引集合。该公式累积了从第一个分箱到当前位置的局部效应，刻画了特征 (x_j) 对模型输出的整体影响。

ALE的金融校准

原始ALE方法生成的是相对于某个未知常数的依赖关系。为使其具有金融意义，作者利用期权定价的边界条件进行校准：

• 当 (S \to 0) 时，(C(S, \sigma, \tau, K) \to 0) （标的无价值时看涨期权无价值）
• 当 (S \to \infty) 时，(P(S, \sigma, \tau, K) \to 0) （标的价格趋于无穷时看跌期权不会被执行）
• 当 (\tau \to 0) 时，价格收敛于内在价值
• 当 (\sigma \to 0) 时，期权退化为远期合约

从ALE到Greeks的有限差分

获得校准后的ALE值后，Greeks可通过有限差分近似得到：

Delta（对标的价格的一阶敏感性）：
[\Delta \approx \frac{\partial \widehat{ALE}_S}{\partial S}]

Vega（对隐含波动率的敏感性）：
[\mathcal{V} \approx \frac{\partial \widehat{ALE}_\sigma}{\partial \sigma}]

Theta（对时间的敏感性，注意负号）：
[\Theta \approx -\frac{\partial \widehat{ALE}_\tau}{\partial \tau}]

Gamma（Delta的二阶导数）：
[\Gamma \approx \frac{\partial^2 \widehat{ALE}_S}{\partial S^2}]

关键区别：与参数Greeks假设“其他变量保持不变”的偏导数定义不同，ALE-based Greeks反映的是条件于实际市场环境的平均边际效应。这一差异使得非参数Greeks能够捕捉市场隐含的真实风险敞口，而非理论化的ceteris paribus敏感性。

实证证据

数据与模型

作者采用两组数据进行验证：

1. 模拟数据：200万条基于Black-Scholes公式生成的欧式看涨期权价格，用于验证方法在理想条件下能否还原理论Greeks；
2. 实证数据：来自OptionMetrics的约1400万条S&P 500欧式期权数据（2018-2022），包含看涨和看跌期权的日终中间价。

机器学习模型采用XGBoost（梯度提升树），通过网格搜索优化超参数。模型输入为标准化后的特征向量 (\mathbf{x})，输出为标准化期权价格 (C/K) 或 (P/K)。

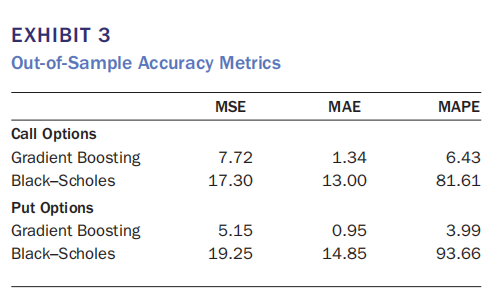
Exhibit 3 说明梯度提升模型在样本外预测中显著优于Black-Scholes模型（MSE、MAE、MAPE三项指标均大幅领先）。

模拟数据验证

在Black-Scholes假设成立的模拟环境中，非参数方法精确还原了理论Greeks。这一结果至关重要——它证明了当数据生成过程符合参数模型时，ALE方法不会引入系统性偏差。

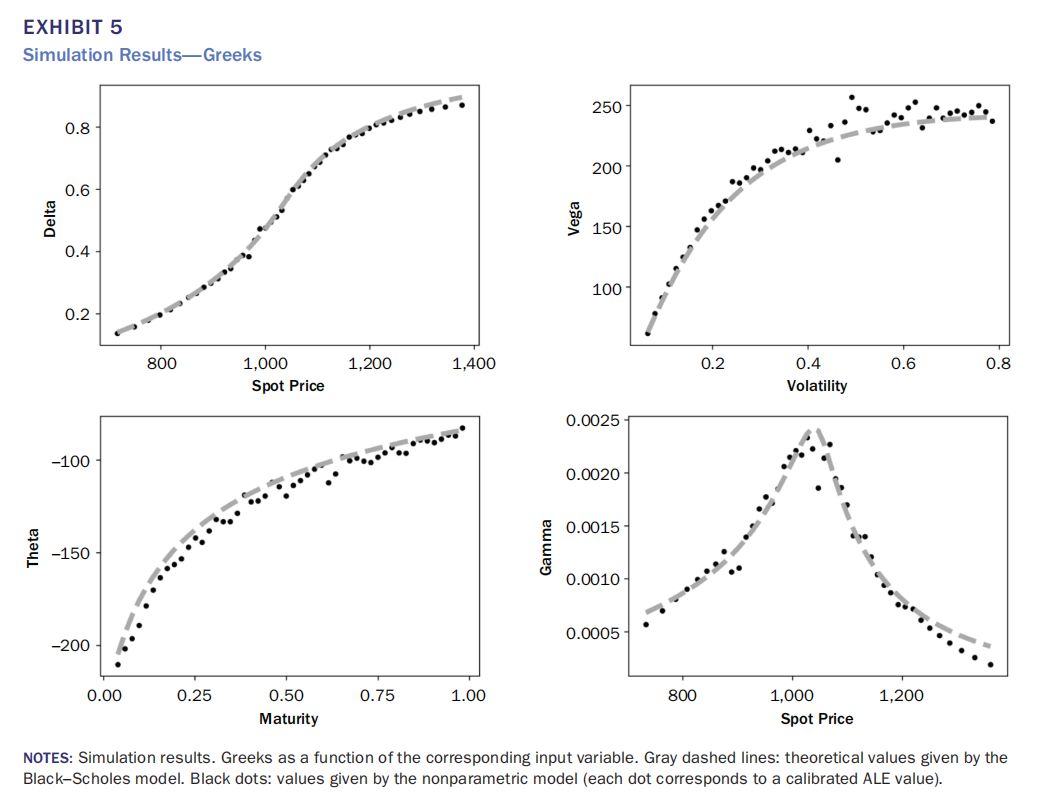
Exhibit 5 说明模拟数据下非参数Greeks（黑点）与Black-Scholes理论值（灰色虚线）的高度吻合，验证方法的理论有效性。

实证数据的关键发现

将方法应用于真实市场数据后，系统性偏离Black-Scholes预测的现象浮出水面：

1. 期权价格的凸性增强

市场价格相对于标的价格呈现更强的凸性，这与实际收益率分布的尖峰特征一致。Black-Scholes模型在整个定价域内系统性高估期权价格，偏差在高波动率和长期限情景下尤为显著。

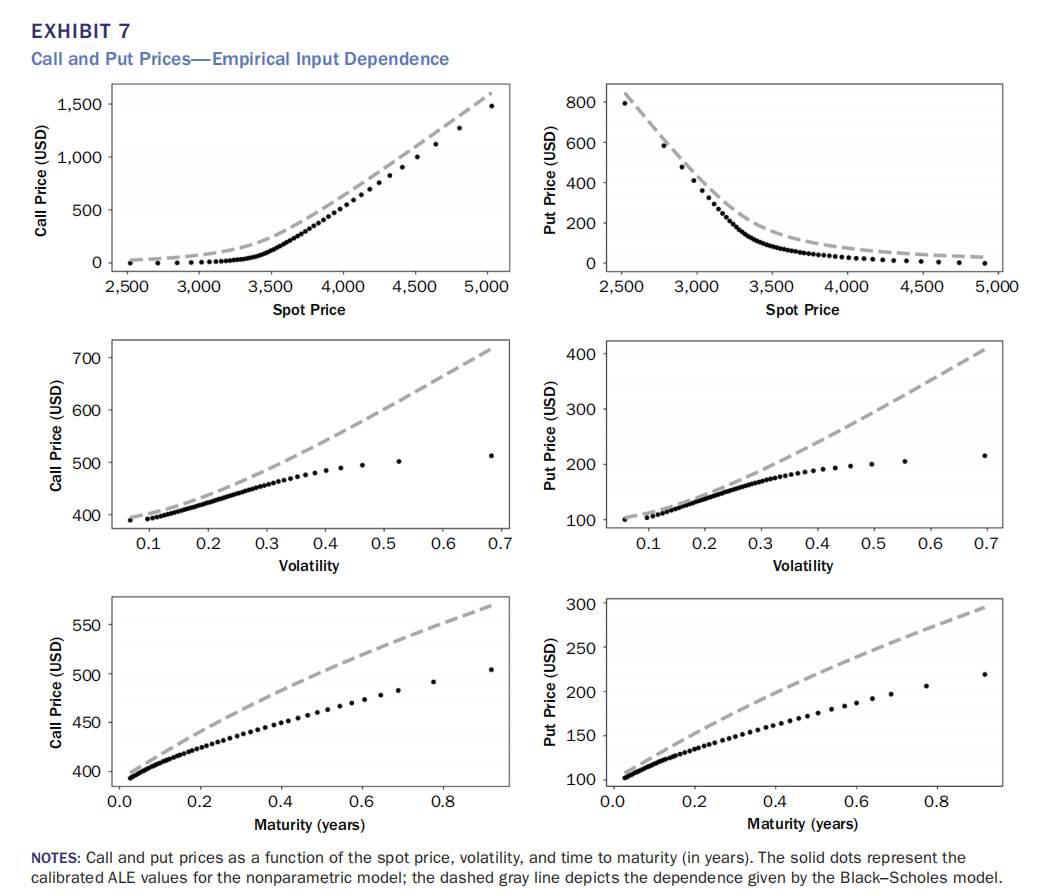
Exhibit 7 上排两图说明看涨/看跌期权价格相对于标的价格的依赖关系，揭示市场价格的凸性显著高于Black-Scholes预测。

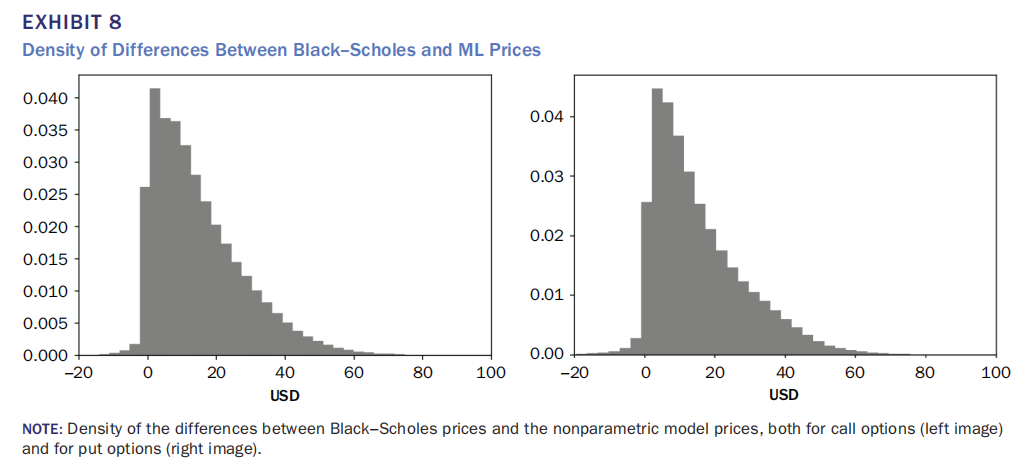
Exhibit 8 说明Black-Scholes模型与机器学习模型定价差异的分布，揭示系统性高估的幅度（均值约为正值）。

2. Vega在高波动率区间趋于饱和

这是最具实践意义的发现之一。Black-Scholes模型预测Vega随波动率单调递增，而市场隐含的Vega在波动率超过0.4-0.5后明显趋于平缓甚至下降。

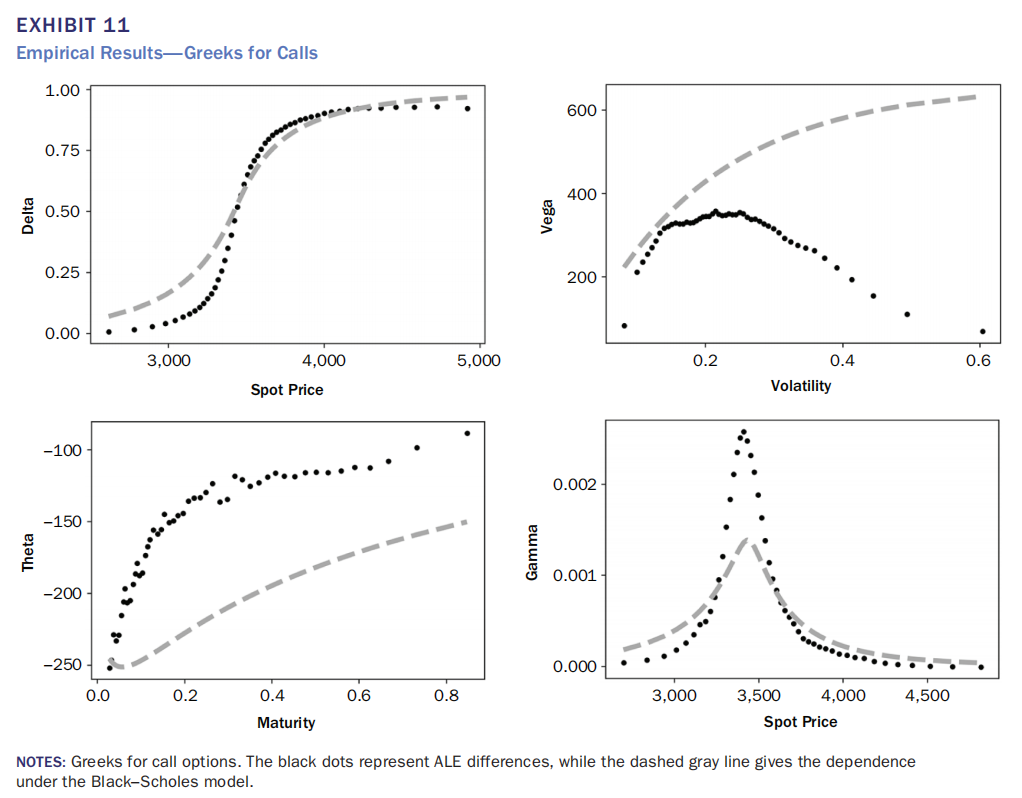
Exhibit 1.1（右上图，Vega vs Volatility） 说明市场隐含Vega在高波动率区间的饱和效应，与Black-Scholes的单调递增预测形成鲜明对比。

这一现象的经济学解释：当波动率已处于高位时，市场参与者可能认为进一步的波动率冲击信息量较低（均值回复预期），或已通过波动率风险溢价将极端波动率的影响折现。从对冲角度看，高波动环境下Vega对冲头寸可能被传统模型高估。

3. Delta曲线更陡峭，Gamma峰值更尖锐

非参数Delta呈现更明显的S形曲线，在平值附近的过渡更为陡峭。相应地，Gamma在平值附近呈现更高更窄的峰值。

Exhibit 1.1 左上图Delta、右下图Gamma 说明市场隐含的Delta曲线陡峭化和Gamma峰值尖锐化现象。

这意味着市场对大幅价格变动的定价比Black-Scholes模型更为敏感，可能反映了尾部风险（如崩盘风险）的溢价。对Delta中性策略而言，平值附近的Gamma风险可能被低估。

4. Theta衰减呈现非线性特征

市场隐含的Theta绝对值普遍小于Black-Scholes预测，且长期限期权的时间衰减速度更慢。

Exhibit 1.1 左下图Theta vs Maturity，用于说明市场隐含Theta的非线性衰减模式与Black-Scholes假设的差异。

这一现象与波动率期限结构密切相关：长期限期权的隐含波动率系统性低于短期限期权（见Exhibit 9），导致其对时间的敏感性降低。

模型推导（简述）

本文的机器学习框架采用梯度提升机作为非参数定价模型。该方法通过迭代地添加决策树来修正前序模型的预测误差：

[
\hat{y}^{(m)}(\mathbf{x}) = \hat{y}^{(m-1)}(\mathbf{x}) + \eta h_m(\mathbf{x})
]

每棵新树 (h_m) 通过最小化正则化损失函数确定：

[
\mathcal{L}^{(m)} = \sum_{i=1}^n l(y_i， \hat{y}^{(m-1)}(\mathbf{x}_i) + h_m(\mathbf{x}i)) + \gamma J + \frac{1}{2} \lambda \sum{j=1}^J w_j^2
]

其中 (l) 为平方误差损失，(\gamma) 惩罚叶节点数量 (J)，(\lambda) 惩罚叶节点权重 (w_j) 的幅度，防止过拟合。

作者利用价格同质性假设对输入输出进行标准化处理：模型学习 (C/K) 与 (S/K, \sigma, \tau) 之间的关系，预测后再乘以执行价 (K) 还原为货币单位。

值得强调的是，虽然本文采用XGBoost实现，但ALE方法本身是模型无关的——理论上可应用于任何机器学习模型，包括神经网络、随机森林等。这为方法的推广应用提供了灵活性。

结论与启示

核心结论

1. 方法论贡献：本文首次将ALE方法应用于期权Greeks估计，提出了一种完全非参数的、数据驱动的风险敏感性度量框架；
2. 经验发现：市场隐含的Greeks与Black-Scholes预测存在系统性偏离——Vega在高波动环境下饱和、Gamma在平值附近更为尖锐、Theta衰减呈非线性——这些偏离与市场微观结构、行为偏差、波动率动态等因素相关；
3. 模型表现：梯度提升模型在样本外预测精度上显著优于Black-Scholes模型，验证了机器学习方法在期权定价中的实用价值。

对量化投资策略的实际建议

1. 对冲策略调整

• Vega对冲：在高波动率环境下，传统模型可能高估Vega对冲需求。建议采用非参数方法重新评估波动率敞口，避免过度对冲导致的成本损耗；
• Gamma对冲：平值期权的Gamma风险可能被低估，特别是短期限合约。应增加平值附近的Gamma监控频率；
• Delta中性策略：考虑到Delta曲线的陡峭化，在标的价格穿越执行价时需更频繁地调整头寸。

2. 定价与做市

• 对于做市商而言，Black-Scholes定价在高波动率和长期限区域系统性偏高，可能导致卖方头寸积累；
• 建议采用机器学习定价模型作为Black-Scholes的补充校准工具，特别是在波动率期限结构倒挂时期。

3. 风险管理

• 传统Greeks无法充分捕捉市场隐含的尾部风险溢价，VaR和ES计算可能低估极端情景下的损失；
• 建议将非参数Greeks纳入情景分析框架，特别关注高波动环境下的Vega饱和效应。

4. 方法扩展方向

• 本文方法理论上可扩展至美式期权、奇异衍生品和结构化产品——这些工具缺乏解析Greeks，非参数方法具有独特优势；
• 结合随机波动率模型与机器学习方法，可能实现参数与非参数的优势互补。

局限性

作者诚实地指出方法的局限：需要大量高质量数据进行训练，在低流动性市场的应用受限；存在过拟合风险（尽管通过正则化缓解）。未来研究方向包括数据高效实现、路径依赖衍生品的扩展、以及与其他资产类别的应用。

随着金融数据量日益增长和机器学习技术不断成熟，这种数据驱动的非参数方法有望成为传统理论模型的重要补充，帮助从业者更精准地度量和应对市场风险。对这类交叉领域研究感兴趣的开发者，可以在 云栈社区 的人工智能与算法板块找到更多相关讨论和资源。