集群行为探秘：从SAC原则到多智能体系统与机器人设计

假设你是电影制片人，你想让电影特效中的鸟群飞得像自然界一样灵活自然，你会为每个个体预设好飞行路线吗？1986年，计算机图形学教授克雷格·雷诺兹为探索更逼真的鸟群动画特效，研究粒子间的运动规则，却意外揭示了复杂系统领域著名的“Boids模型”。

国庆阅兵时，自家的小鸽子是跟着邻居飞走了，还是“拐带”了新成员回家？鱼群在海中游弋，真的有固定的领导者吗？当面对多种方向选择时，鱼群会游向何方？在研究令人揪心的踩踏事故时，为何在出口处合理设置障碍柱反而能打破拥堵、加快疏散速度？

从夜空中绚烂的无人机表演，到阅兵式上震撼人心的无人系统方阵，这些科技奇观背后的集群系统隐藏着怎样的奥秘？古人云“道法自然”，此处的“道”，或许正是那套贯穿于自然生物与人造系统之间、支配着个体互动与群体涌现的底层法则。

关键词：自组织、生物集群的多主体建模、唯像描述、集群实验与应用

唯像描述

谈到自然集群，动物行为学研究者必然会进入我们的视线。动物学不算小众，但具体到物种和行为方向则各不相同。当研究行为的学者偶尔感慨“做行为就是写观察日记”时，一个听起来有些跨界的场景出现了：一群理论物理或应用数学的研究者，纷纷携手自己钟情的动物，登上了顶尖期刊的封面。

这群人也可以这样形容：一群系统科学的研究者，以“唯像描述”为起点，将鱼群、鸟群、蚁群、蝗虫群、蜂群等各种动物群体，带到了《自然》（Nature）、《科学》（Science）等顶级期刊的封面上。

那么，究竟什么是唯像描述？

何为唯像描述？

唯像理论，是指“解释物理现象时，不探究其内在原因，而是使用概括试验事实得到的物理规律”。唯像理论是实验现象的提炼与概括，但尚无法用已有的科学理论体系做出完全解释。

对于集群运动，基于观察或实验直接得到的宏观（群体）层面的规律，便是集群运动的唯像理论。然而，目前尚缺乏足够普适的唯像理论，在不同的实验条件下往往得到不同的规律，因此称之为集群运动的“唯像描述”更为妥当。

唯像描述在科学史上具有重要意义：

约翰内斯·开普勒在17世纪初提出的行星运动三大定律，就是基于天文观测的归纳总结。开普勒没有深入解析行星运动背后的力学原因，而是通过观察和归纳得出规律：

1. 轨道定律：行星沿椭圆轨道围绕太阳运动，太阳位于椭圆的一个焦点上。
2. 面积定律：行星与太阳的连线在相等时间内扫过的面积相等。
3. 周期定律：行星轨道周期的平方与其轨道半长轴的立方成正比。

这些规律仅是基于观测的总结，并未揭示行星运动背后的动力学原因。从这个意义上说，开普勒的工作体现了唯像理论的精髓——依赖实验事实和观察，而非深入探讨引力的本质。

后来，牛顿在《自然哲学的数学原理》中提出的万有引力定律，成功解释了开普勒的行星运动定律，揭示了这些运动背后的原因——引力。

在集群运动研究中，科学家们常常遇到类似情境。实验中观察到的群体行为（如鸟群、鱼群或人群的运动）可以用某些规律来描述，但这些规律未必揭示了行为背后的微观机制。甚至在不同的实验条件下，可能会得出不同的集群行为规律。此时，我们可以称这些观察到的规律为“集群运动的唯像描述”。

例如，研究者可能发现集群的密度、速度、相互作用等影响整体表现，但并不知道这些表现的内在物理或生物机制。唯像描述提供了一种总结和预测这些复杂现象的工具，但仍需要进一步的研究来揭示其本质。微观机制的科学性大致取决于两点：它本身得到什么程度的实证支持，以及由该机制推演出的理论结果得到什么程度的实证支持。后文中Couzin关于群体中“有思想”个体的研究，先在《自然》上发表理论工作，后续又有猿类生物学家给出了实证分析，堪称微观机制研究的巧合与典范。

唯像描述的数学工具

研究者们发展了一系列数学工具来量化描述集群行为：

1. 个体的运动方向向量：
   
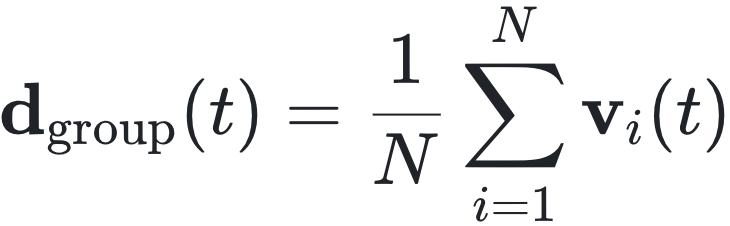
   其中，N 是粒子数，v_i(t) 是第 i 个粒子在时间 t 的速度向量。这个方向向量代表了从群体中心 c_group(t) 指向群体的整体运动方向。

2. 群体极化度：
   
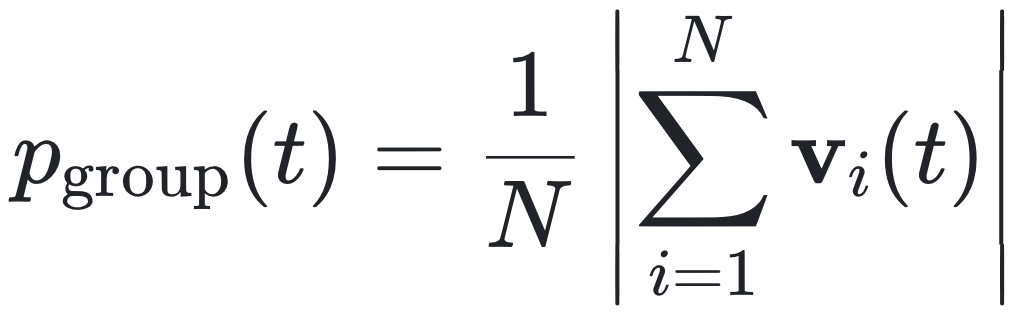
   用来度量粒子群体整体方向的一致性，反映了群体运动的极化程度。在生物研究中，Iain Couzin对鱼群做了类似的建模：极化序参量 O_p。
   
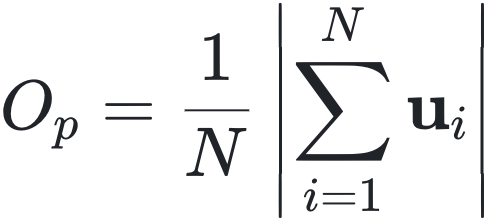
   其中，u_i 是鱼 i 的单位方向向量。O_p 的值在 [0, 1] 之间：O_p = 0 表示没有平均对齐（即无序）；O_p = 1 则表示所有个体完全对齐（即有序）。

3. 群体角动量：
   
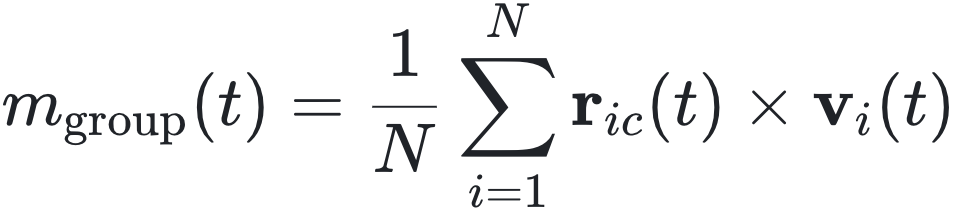
   提供了集体旋转运动的量度。其中，r_ic 是从集体中心到第 i 个粒子的位置矢量：r_ic = c_i - c_group。集体中心位置计算公式：
   
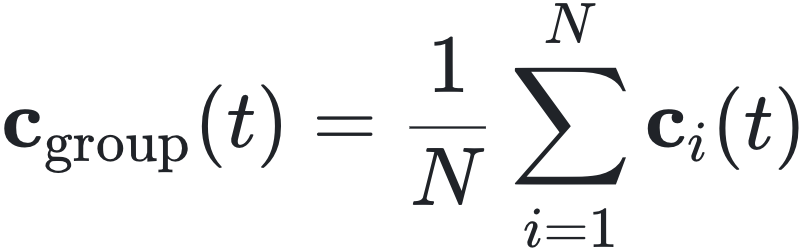
   其中，c_i(t) 是第 i 个粒子在时间 t 的位置向量。
   质心 c_group 被定义为全部个体位置向量的平均值：
   
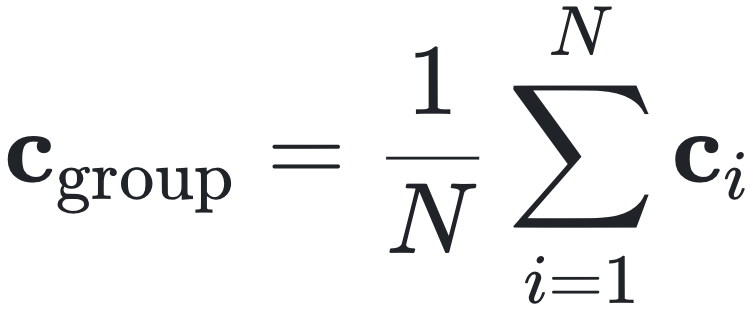
   类似地，有旋转序参量 O_r。
   
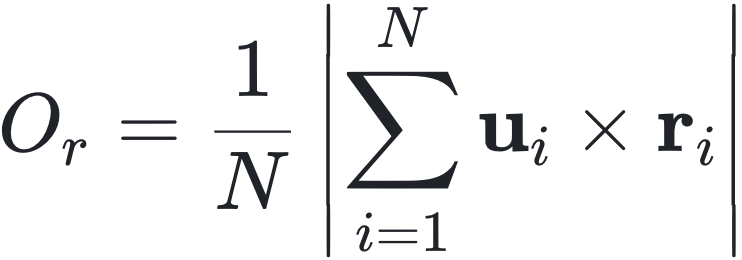
   其中，r_i 是一个单位向量，指向个体 i 相对于质心的方向。
   
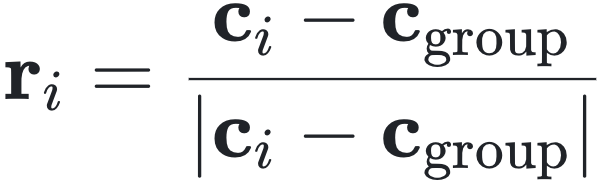
   其中，|c_i - c_group| 是从群体质心到个体 i 的距离。

4. 集群对称破缺：
   Altshuler等人在2005年对蚂蚁进行的实验发现，当实验平台有两个出口时，蚁群在疏散时会出现使用一个出口多于另一个的对称破缺现象。研究发现，正常情况下，蚂蚁从两个出口出去的数量基本相等；但若在中间放置驱虫剂（如香茅油），蚂蚁出于恐慌会集中从一个出口疏散，导致某个出口的疏散数量明显多于另一个，这就是一种对称破缺现象。

5. 集群规模与集群数量：
   描述了系统中形成的子集群的特征，集群规模通常定义为其包含的个体数量。

6. 空间关联与标度律：
   空间关联分析用于研究个体间位置和运动的相互影响，可以联想信号处理中的自相关与互相关函数来理解。
   空间关联函数 C(r) 通常表示为：
   
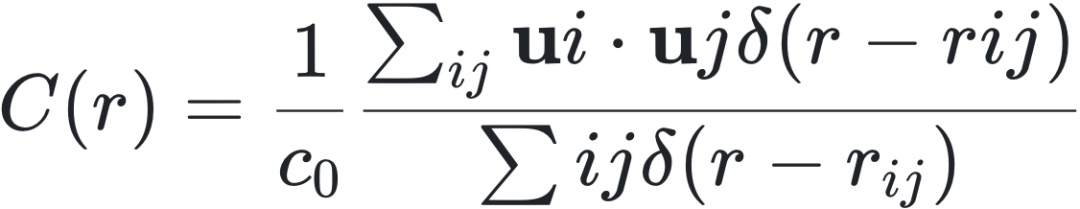
   其中 δ(r - r_ij) 是一个平滑的 Dirac δ-函数，用于选择相互距离为 r 的“个体对”，u_i · u_j = u_ix u_jx + u_iy u_jy + u_iz u_jz，c_0 是一个归一化因子。
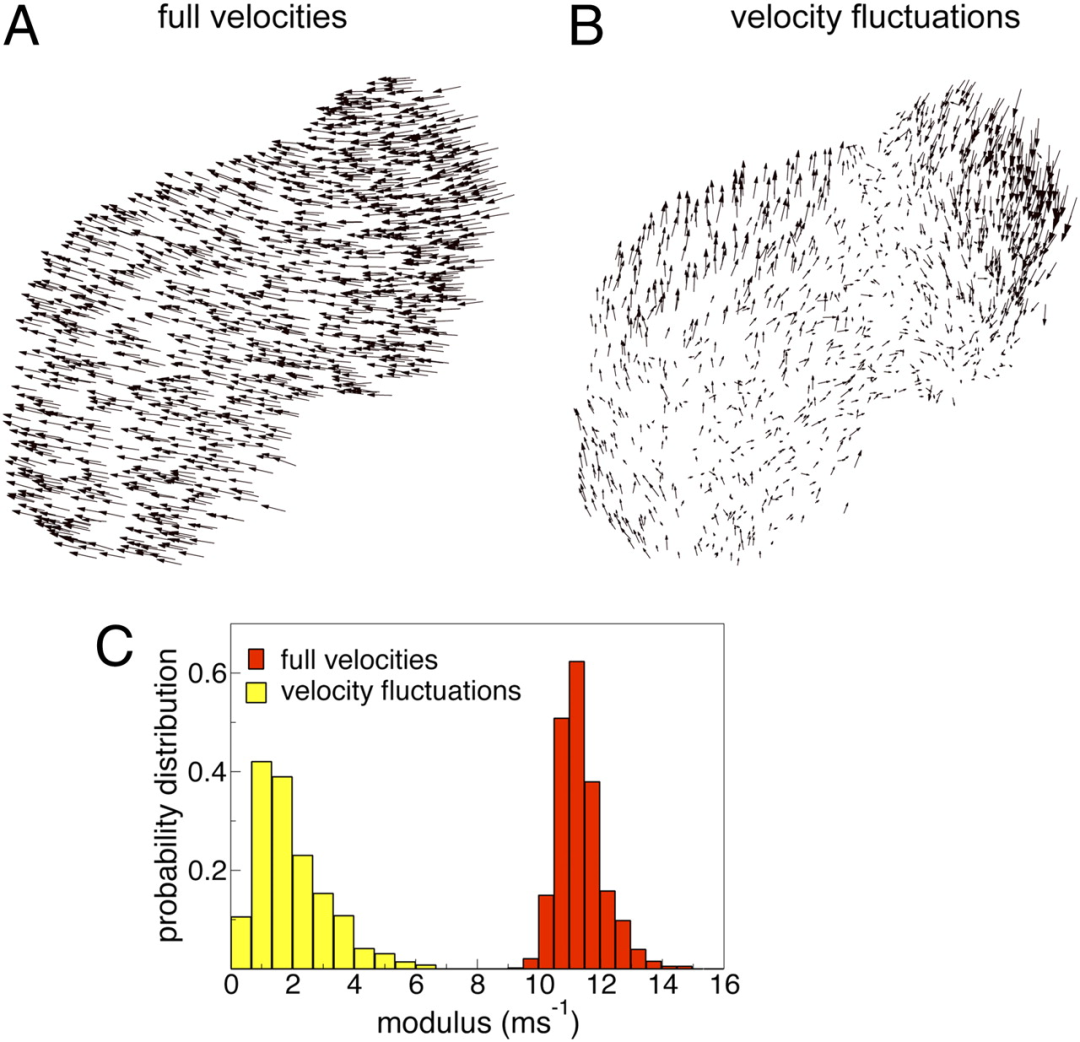
   相关函数测量个体在距离 r 处的速度波动的平均内积。C(r) 的大值意味着波动几乎是平行的，因此强相关；负值意味着反相关；平均值趋近于零则意味着不相关。

空间关联研究的是这样的问题：一个动物的行为状态变化，会影响并受到群体中其他所有动物行为状态变化的影响，他们互相影响的尺度是怎样的？比如，鱼群中的一个个体是只能影响周围邻居，还是能影响整个群体（无论群体规模多大）？

标度是指系统特征与其规模（如大小、长度、时间等）之间的关系。标度性主要分为以下几类：

1. 无标度：描述系统中某些特征不随尺度改变而变化。例如，无标度网络中的节点连接数遵循幂律分布。在动物群体行为中，无标度行为关联意味着个体的行为会影响其他个体，无论群体的大小如何。
2. 标度变化：指随着系统规模的变化，其特定性质或行为表现出一定的规律性。
3. 分形：在不同尺度上都显示出相似的模式，具有自相似性。

集群实验

鱼我所欲

法国图卢兹大学的泰赫拉斯教授与北京师范大学的研究人员合作，展开了一项关于鱼群U-turn（转向）行为的实验和模型研究。实验在一个环形鱼缸中进行，使用相对较少的水以确保鱼群在二维平面上游动（由于环形设计，可近似理解为一维空间）。

研究者选择了数量较少的鱼群（仅5条），以便深入观察个体间的相互作用。当鱼群数量较多时，观察和建模个体互动会变得复杂，因此通过较少数量的鱼来具体验证假设。

在实验中，5条鱼在鱼缸中游动时，其中一条会突然转向反方向游动。这会影响到其他鱼，使它们也开始折返，从而形成整个鱼群的U-turn现象。研究团队通过分析，识别出在这些相互作用中，哪条鱼对其余鱼的行为影响最大，并对影响力进行排序，揭示了“领导者”的存在。

后续研究进一步采用机器人模型来模拟鱼群游动。通过构建相应模型指导机器人实验，发现仅需一条具有最大影响力的“鱼”，即可使机器人群体表现出与真实鱼群相似的U-turn行为模式。

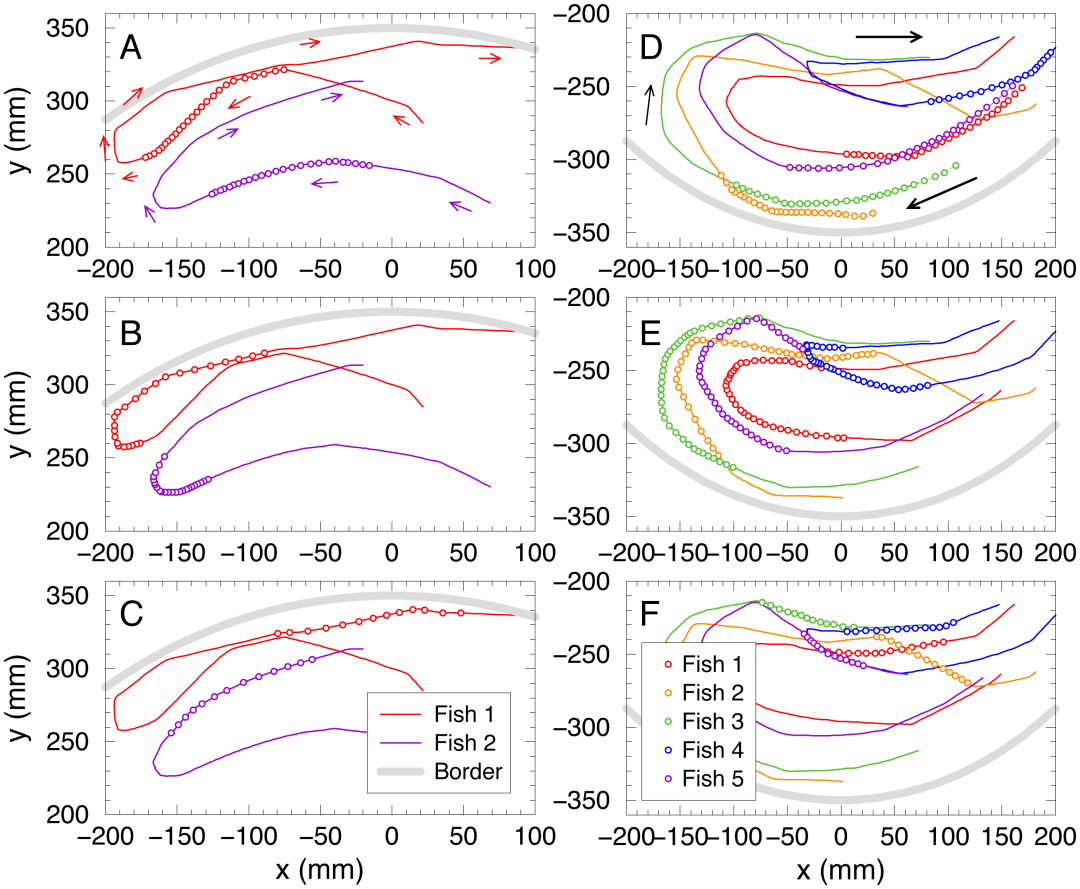
下文在Couzin模型中，也有鱼群的身影。我国系统科学的领军高校北京师范大学也有一支团队（韩战钢教授团队）围绕复杂系统视角下的鱼群开展了系列研究。

鸽（各）有鸽（各）意

匈牙利学者T. Vicsek等人进行了一项关于鸽子群体飞行的实验。他们在鸽子身上安装了小型差分GPS系统以跟踪飞行信号。结果显示，鸽子在飞行时出现了前面一只领头飞行，后面的鸽子逐级分化为次领和跟随者的社会结构。

在另一项鸟群飞行实验中，戴维·桑普特等人将鸽子从巢穴分别在10英里和20英里的距离处放飞。他们发现单只鸽子的归巢过程各不相同，有些能直线飞回，有些会绕路，还有一些飞得非常远（被称为“crazy bird”）。

研究人员随后将鸽子成对放飞观察。发现当将沿着短路径飞回的鸽子与“crazy bird”一起放飞时，开始时两只鸽子会跟随“crazy bird”飞行，但经过一段时间后，识路的鸽子最终会意识到方向错误，从而在半道上折返，直接飞回巢穴。这一现象反映了在知识共享的情况下，鸽子个体之间如何进行合作与决策。

蚁亦有慧

实验人员在蚂蚁觅食的路径上搭建了一个可折叠的小桥，利用几个关节控制桥的高度和角度。当蚂蚁通过小桥抵达食物源并搬回巢穴后，经过一两次往返，它们会在小桥的中间位置，自组织地搭建起一座蚁桥。

蚂蚁能够根据实际需要调整搭建蚁桥的高度。因为如果搭建得过高，蚂蚁需要走的路径会变长；而如果搭建得过低，则需要使用更多的蚂蚁来搭建桥梁。这个实验展示了蚂蚁在觅食过程中的自组织能力，能够通过调整高度达到一个最优的平衡状态。

集群运动的理论建模

群集运动建模主要有两种方法：

第一种是基于群体的宏观方法，其建模对象为整个群体，采用偏微分方程来描述群体密度场和速度向量场的反应-扩散现象，据此研究群体整体的稳定性和运动性质。该方法通常不考虑个体的具体交互行为，因而不能从个体视角分析群体行为。

第二种是基于个体的微观方法，其建模主体为个体，通过常微分方程（连续型）或差分方程（离散型）来描述个体的运动及交互规律，可同时考虑运动随机性、外部环境影响、个体的生理及心理特异性等诸多现实因素，因而是对群集最直观和自然的一种建模方法。微观群集模型均是在探讨群集运动的发生机理问题，即个体遵循什么样的局部交互规则才能产生协调有序的宏观群集运动。

西北工业大学的刘明雍老师给出了如下分类：

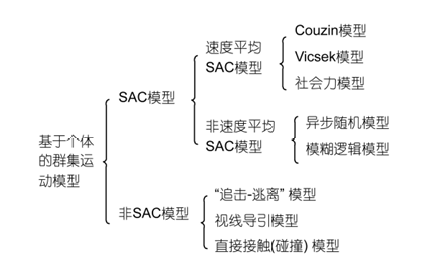
SAC原则是指：
(1) 避撞：避免与邻近个体发生碰撞。
(2) 结队：与邻居运动方向保持一致。
(3) 聚集：向周围邻居靠拢。
这三者共同作用，便可模拟出与实际鸟群或鱼群颇为相似的集体运动形式。

实际上，SAC这个名称源于Boids模型。Boids模型源自Reynolds在1986年发表的重要论文《Flocks, Herds, and Schools: A Distributed Behavioral Model》。

Boids模型

Boids（bird-oid object），是一种模拟鸟集群行为的计算机算法。克雷格·雷诺兹是一位计算机科学家，以其在计算机图形学和人工智能领域的工作而闻名，尤其是他于1986年提出的“Boids”模型。这个模型模仿了鸟类群体的运动，成为群体行为模拟中的经典案例。

当时研究计算机动画的Reynolds等人希望计算机动画中的鸟群不要飞得太不自然，他们希望能像自然界的鸟一样，做到自然生动。2026年电影《哪吒之魔童闹海》的导演饺子看到此模型，大概要大呼同道中人。

可以讲，这是电影人对真实自然的跨越时空的共同追求。

1986年的Reynolds提出：鸟在飞行时互相不能离得太远（否则形不成鸟群），也不能距离过近（否则会相撞），在距离适中的情况下，鸟儿们要对齐飞行。这样就可以形成计算机动画中比较自然的鸟群飞行状态。这就是上文所简称的SAC原则，也是Boids模型的核心思想。

而在2026年，从央视对哪吒团队的采访中，我们发现电影中“束缚所有海妖的锁链”这一名场面的达成也有集群行为的身影（电影制片人刘潘提到：“锁链如何跟这些海妖交互，就是一锅粥…导演想要的是乱中又有序，还要好看。锁链要像头发丝一样在空中随着风，有点微弱的摇曳感。”）。

Boids模型在计算机图形学、游戏开发、生物学研究、机器人学等领域得到了广泛应用。

Vicsek模型

Vicsek模型是一种用于模拟自组织运动的二维动力学模型，由物理学家 Tamas Vicsek 及其合作者在1995年提出，旨在研究简单的局部交互如何导致复杂的全局行为。

模型的基本假设为：每个粒子在每个时间步长 t 更新其位置和方向：X_i(t + 1) = X_i(t) + V_i(t) Δt。其中 X_i(t) 是第 i 个粒子在时刻 t 的位置；V_i(t) 是其速度；Δt 是时间步长。

粒子在每个时间步长的运动方向更新公式：θ(t + 1) = 〈θ(t) 〉_r + Δθ。其中 〈θ(t) 〉_r 是距离为 r 的邻域内所有粒子的平均方向。Δθ 是一个随机扰动。

Vicsek模型展示了在简单的局部交互规则下，粒子如何自发形成有序的集体运动（如线性运动、旋转或更复杂的形状）。

微观群集模型围绕着局部交互规则产生协调有序的宏观群集运动展开，提出交互规则只是完成了思考的一部分，根据规则产生的结果则进一步佐证了该规则是否合理。

Couzin三区模型

Iain Couzin是一位著名的进化生态学家和动物行为学家，他提出了著名的Couzin模型。

Couzin认为每个个体试图在“排斥区”（zone of repulsion, zor）内与其他个体保持一个最小距离，该区域建模为一个以个体为中心、半径为 r_r 的球体。如果在时间 t 时，排斥区内存在 n_r 个邻居，个体 i 的反应是远离这些邻居。

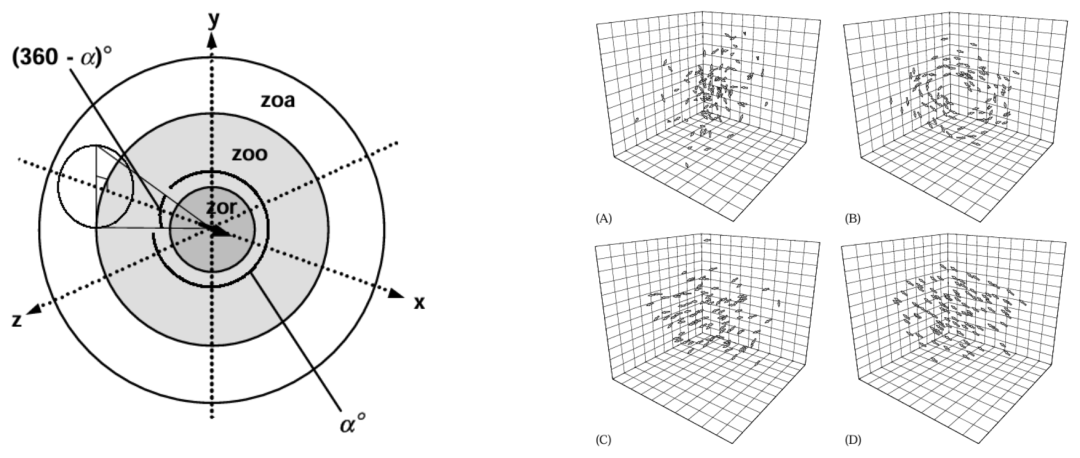
• “zone of repulsion” (zor): 排斥区，个体试图保持距离以避免碰撞。
• “zone of orientation” (zoo): 定向区，个体感知周围其他个体并调整方向的区域。
• “zone of attraction” (zoa): 吸引区，个体感知并朝向其他个体的区域。
• “blind volume”: 个体无法侦测到其他邻居的盲区。

在模型中，“排斥区”的行为规则优先级最高。
如果存在邻居（即 n_r > 0），那么个体的期望方向 d_i(t + τ) 将采用排斥区的计算结果 d_r(t + τ)。

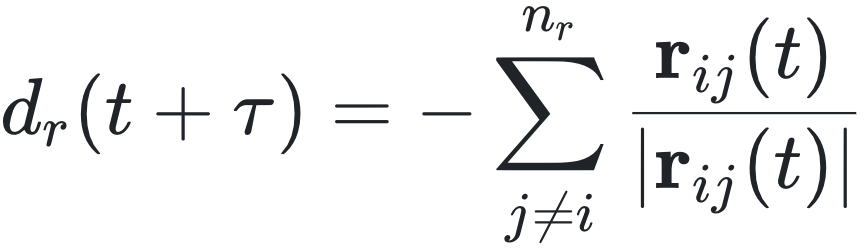
这一公式描述了个体 i 在时间 t + τ 的期望方向 d_r(t + τ)，是通过计算在“排斥区”内其他 n_r 个体的位置向量的合成，负号表示个体 i 会朝远离其他个体的方向移动。

如果在排斥区不存在邻居（即 n_r = 0）

• 如果邻居仅在定向区中（即 n = n_o），那么个体 i 的期望方向将由定向区决定：d_i(t + τ) = d_o(t+τ)。
• 如果邻居仅在吸引区中（即 n = n_a），那么个体 i 的期望方向：d_i(t + τ) = d_a(t+τ)。
  
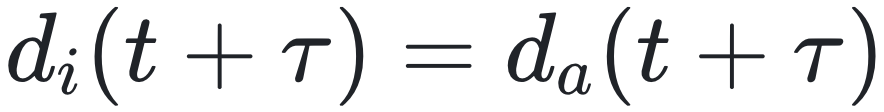
• 如果邻居同时出现在两个区域，个体 i 的期望方向将是两个方向的平均值：
  

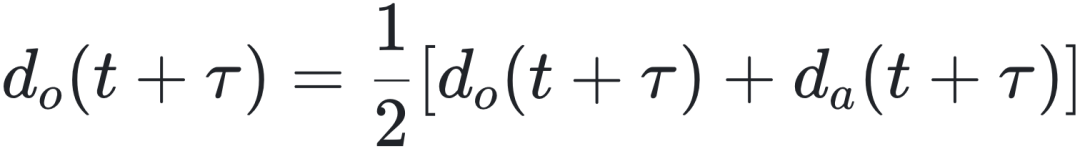
群集运动最突出的特征是大量个体能保持运动方向的协调一致，在SAC规则中，这主要由结队运动完成。根据结队运动实现方式的不同，SAC模型可分为两类：
(1) 基于“速度平均”的SAC群集模型：个体参照周围邻居的平均速度（方向）调整自身速度（方向）。
(2) 非速度平均SAC群集模型：采用随机耦合、选择耦合、模糊逻辑等“非平均化”方式实现结队运动。

Couzin有知识个体*个人影响力模型

Couzin考虑到个体的聚合能力，每个个体能根据周围邻居的运动（社交互动）来调整自己的运动。

模型假设：群体由 N 个个体组成。每个个体具有位置向量 c_i(t)、方向向量 v_i(t) 和速度 s_i，并试图在任何时候与个体 i 及其他个体 j 之间保持最小距离 α，通过远离该范围内的邻居来实现。

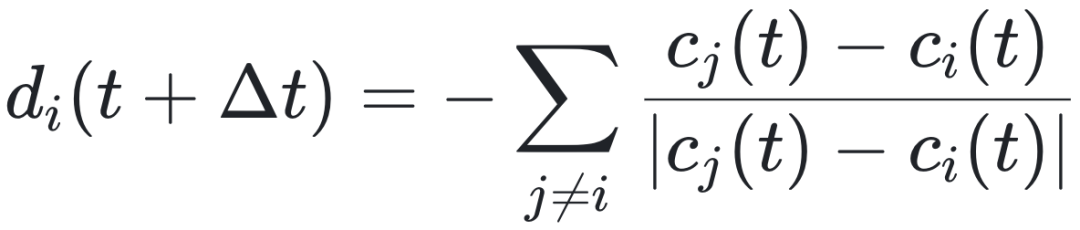
其中 d_i 代表期望的移动方向。避免碰撞是最高优先级。如果在该区域内没有检测到邻居，那么个体将倾向于与局部交互范围 ρ 内的邻居对齐。

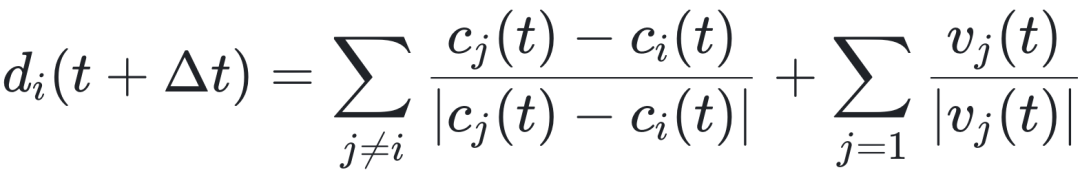
这里 d_i(t + Δt) 被转换为相应的单位向量 d̂_i(t＋Δt) = d_i(t＋Δt)/|d_i(t＋Δt)|。

为了考虑“知情”个体的影响，部分个体 p 被赋予关于偏好方向的信息（模拟为单位向量 g）。所有其他个体都是“天真”的，没有朝向特定方向的偏好，也不知道群体中哪些个体拥有信息。知情个体通过权重项 ω 平衡其偏好方向和社交互动的影响，并将 d̂_i(t＋Δt) 替换为 d'_i(t＋Δt)，其中：

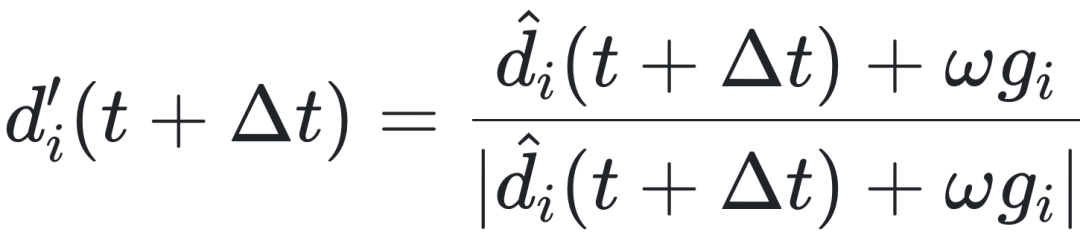
此时Couzin研究的问题是：如果一群个体中有一部分知道了“独家消息”，那么这部分个体的数目和个体影响力（权重）怎样的配置能够引导整个集体？如果有知识的个体做出的决策不一样，怎样的配置能够把群体分开呢？

2005年的《自然》杂志高度认同Couzin的这一理论方向，并给出了封面报道。而在2015年，《科学》杂志对此给出了实证的结果。

Cucker-Smale模型

CS模型是一种使用微分方程来描述自驱动粒子群体行为的数学模型，最早在2007年提出，专注于描述粒子之间的相互作用以及如何通过这些交互产生集体运动：
dx_i/dt = v_i

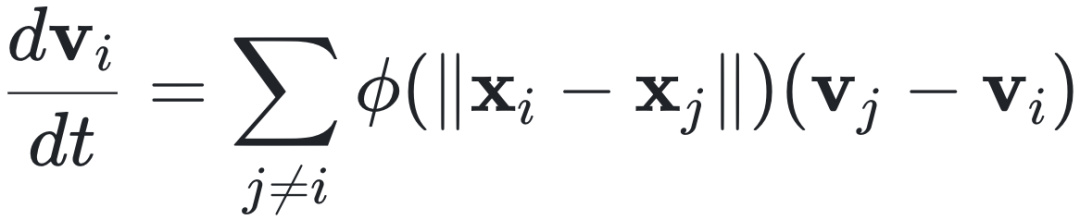
其中，x_i 是粒子 i 的位置，v_i 是其速度。Φ 是一个相互作用函数，通常依赖于粒子间的距离 ||x_i - x_j||。相互作用函数 Φ(r) 可以设置为：

• 短程相互作用（例如，作用范围有限）：
  
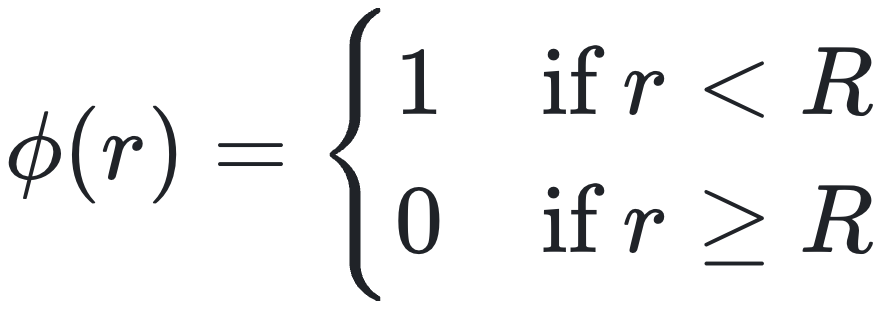
  其中 R 是粒子相互作用的范围。
• 光滑的相互作用（例如高斯型）：
  
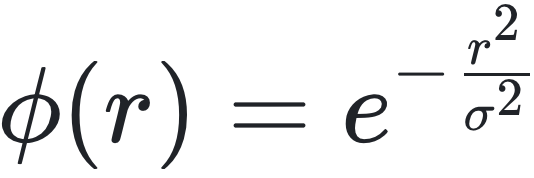
  这里 σ 是与作用强度相关的参数。

通过Cucker-Smale模型，可以观察到一致性、相变、极化等集体行为特征。该模型的一个重要特性是其系统的稳定性：在满足一定条件（如相互作用强度充足且在有限距离内）下，粒子群体最终会收敛到一个统一的速度和方向。

追逃问题

在集群行为研究中，追逃是一个重要问题。追逃现象在自然界和人工社会中频繁出现，包括动物之间的围捕。

莫斯科大学的研究学者通过理论研究表明，在一个格点空间中，若多个移动速度相同的捕食者追捕一个被捕食者：

• 当捕食者随机游走且视觉距离有限时，被捕食者在一定距离外应保持不动，待其临近时再移动。
• 当捕食者具有持续视觉能力时，数学计算表明，需要三只捕食者才能围捕住一个被捕食者。

当捕食者和被捕食者都是多对多的情况时，严格的数学解尚未得出。有东京学者研究指出，追捕者数量增加时，逃跑者的整体生存时间会下降。但捕食者的数目并非越多越好，群体数目过大时，整体的追捕效率反而会下降。

追逃问题对于捕捞学、航海等领域的研究者可能有天然的吸引力，希望本文能带来一点新的思考。

应用

所谓自组织，是指群体的有序时空结构或模式产生自个体之间的局部交互，而非外部指导、操作或全局集中控制的结果。这与无人系统中常见的外力驱动编队问题有本质不同。

行为应用·人群疏散

集群行为在人类中的一个典型现象是：拥挤踩踏事件。历史上多次踩踏事件造成了严重伤亡。

针对紧急事件中的人群疏散规律，多个国家已开展相关研究。研究发现，通过算法（如遗传算法）优化设计的封闭空间疏散通道可以显著提高效率。例如，在门口设置圆柱障碍物被证明能有效促进疏散。相关模拟实验表明，在80人聚集的体育馆中，设置不同数量障碍物对疏散速度有明显影响。

D. Helbing等人研究人群疏散时发现，在一个有两个出口的场馆中，人群会更倾向于使用其中一个出口。总体来说，正确设计疏散通道，尤其是在拥挤场景中，能够有效降低人群横向剪切力，促进更快速的疏散。这一研究发现被简化为“出口设柱，疏散快16%”被多家媒体报道。国际著名的咨询公司兰德公司在为卡塔尔世界杯做咨询时，也将此研究成果纳入了其报告，建议场馆设计遵循这样的原则。

算法

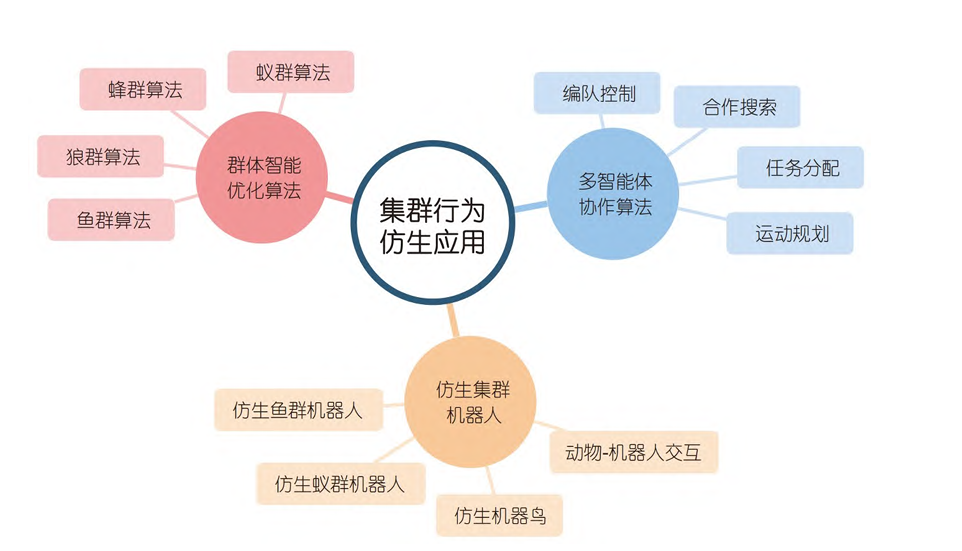
群体智能优化算法是一类启发式优化算法，灵感来源于群体行为中的集体智能。这类算法通过模拟生物体群体（如蚂蚁、鸟群、鱼群等）在求解问题时的协作来进行优化搜索。

粒子群算法就是一种基于群体智能的优化算法，由James Kennedy和Russell Eberhart于1995年提出。其核心思想是通过个体（粒子）间的社会信息共享（个体经验与群体经验）实现对非线性函数的优化。PSO算法结合了进化计算和群体智能的特点，具有简单性、低计算成本和广泛适用性等优势。

除粒子群算法外，还有人工鱼群算法、蚁群算法、鲸鱼算法等。群体智能算法在电影动画行业也有深远影响。以电影《哪吒》中的片段为例，在“洪流之战”中，大量妖兽的群体智能行为是通过分布式消息队列和Swarm算法等技术实现的。

集群机器人

与生物集群类似，集群机器人系统具备如下5个主要特点：

1. 系统由可自由运动的机器人组成。
2. 机器人可感知并改变周围环境。
3. 机器人功能相对简单，感知与通信能力有限。
4. 系统无中心控制、个体无全局信息。
5. 机器人通过合作形成群体以完成特定任务。

上述特征使集群机器人相比中心控制系统具备高鲁棒性（容错能力强）、可扩展性（规模变化不影响性能）和灵活性（能完成多种任务）等优势。

集群机器人基于行为的设计方法主要为2种：
(1) 虚拟物理力：机器人被抽象为物理实体，个体之间存在排斥、吸引与对齐等相互作用力，通过调节作用力参数实现宏观集群现象。例如Khatib等最早提出的人工势场概念。
(2) 随机有限状态机：将机器人的行为方式抽象为若干状态（如随机运动、静止等），机器人可在不同状态之间以一定概率进行转换。Sahin等给出了PFSM方法的典型形式，通过预先给定状态转移概率可实现机器人的聚集。

为了评价设计方法的性能，学者们提出了3种主要分析方法：
(1) 计算机模拟：借助计算机模拟环境与交互，验证设计方法的可行性并进行优化。
(2) 动力学模型：通过随机过程、动力学方法等经典理论工具验证设计方法的收敛性。
(3) 机器人实验：在实际机器人系统中验证设计方法的可行性与鲁棒性，这是必要手段。

希望本文对集群行为从理论到应用的介绍，能为大家在计算机科学与工程实践领域带来一些启发。关于更深入的讨论，欢迎在技术社区如云栈社区等平台交流。

参考文献

• 李耕，狄增如，韩战钢. 集群运动：唯像描述与动力学机制[J]. 复杂系统与复杂性科学， 2016， 13(002):1-13.
• Kolbjørn Tunstrøm, Yael Katz, et al. Collective States, Multistability and Transitional Behavior in Schooling Fish[J]. PLoS Computational Biology, 2013， 9(2):e1002915.
• Huang C ， Ling F ， Kanso E .Collective phase transitions in confined fish schools[J].Proceedings of the National Academy of Sciences, 2024， 121(44):8.
• Couzin I D .Collective cognition in animal groups[J].Trends in Cognitive Sciences, 2009， 13(1):36-43.
• Tamás Vicsek, et al. Collective motion[J].Physics Reports, 2012， 517( 3–4):71-140.
• Couzin I D , Krause J , James R ,et al.Collective memory and spatial sorting in animal groups.[J].Journal of Theoretical Biology, 2002， 218( 1):1-11.
• Reynolds C W .Flocks, Herds, and Schools: A Distributed Behavioral Model[J].ACM SIGGRAPH Computer Graphics, 1987， 21(4):25-34.
• Cavagna A , Cimarelli A , Giardina I ,et al.Scale-free correlations in starling flocks[J].Proceedings of the National Academy of Sciences, 2010， 107(26):11865-11870.
• 刘明雍，雷小康，杨盼盼，等. 群集运动的理论建模与实证分析[J]. 科学通报， 2014(25):20.
• 雷小康. 从组群到分群：自组织群集运动的理论建模与分析[D]. 西北工业大学，2015.
• Vicsek T， Czirók A， Ben-Jacob E， et al. Novel type of phase transition in a system of self-driven particles[J]. Physical review letters， 1995， 75(6): 1226.
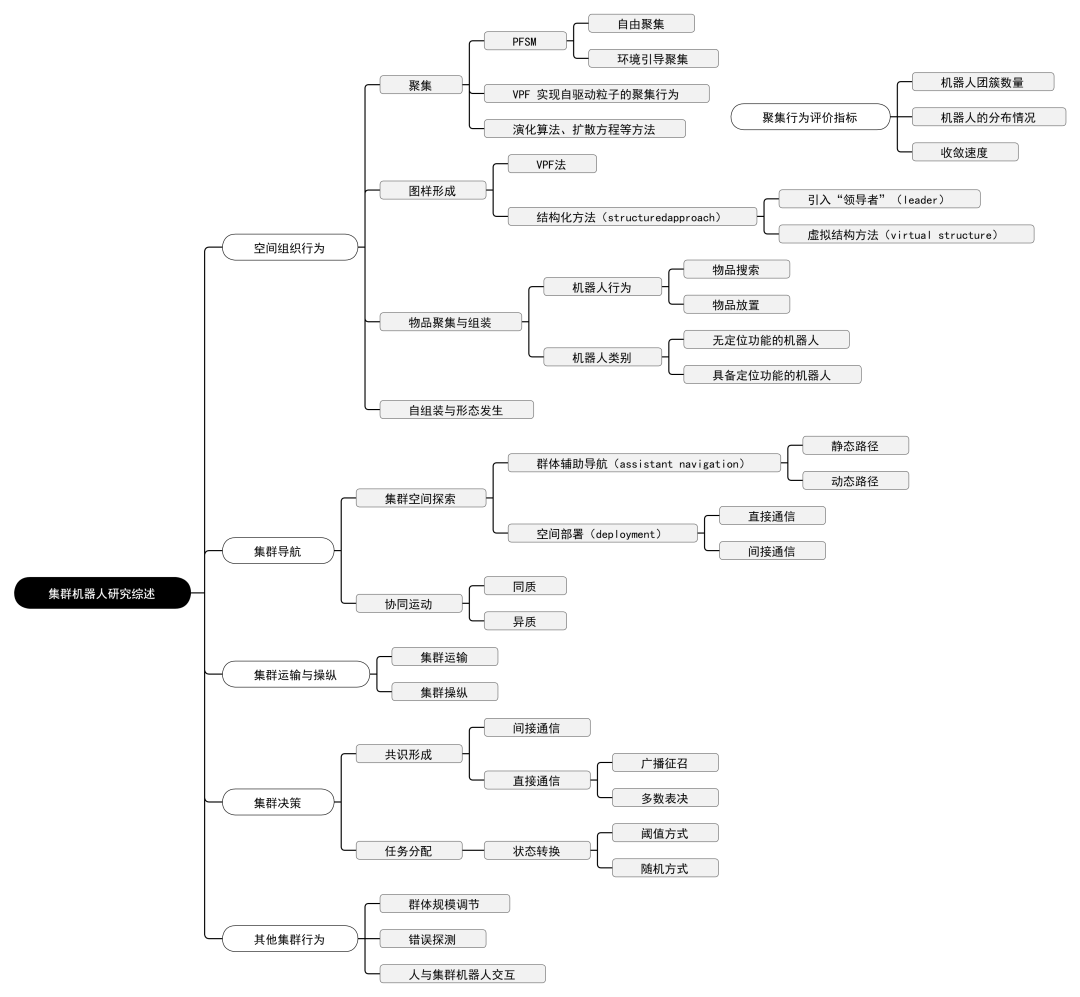
• 王伟嘉，郑雅婷，林国政，等. 集群机器人研究综述[J]. 机器人， 2020， 42(2):25.
• Helbing，Dirk，Farkas，et al.Simulating dynamical features of escape panic.[J].Nature， 2000.
• E. Altshuler; et al. (2005). "Symmetry breaking in escaping ants". American Naturalist. 166 (6): 643–649.
• 刘小峰，陈果，刘宇，等. 动物集群行为的机制和应用[J]. 科学通报， 2023， 68(23):3063-3076.
• Khatib O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International Journal of Robotics Research， 1986， 5(1): 90-98.
• Soysal O， Sahin E. Probabilistic aggregation strategies in swarm robotic systems[C]//Swarm Intelligence Symposium. Piscataway， USA: IEEE， 2005: 325.