刚刚,何恺明团队在arXiv上发布了一篇题为《Generative Modeling via Drifting》的论文,提出了一种全新的生成模型范式——漂移模型(Drifting Models)。

这篇论文的第一作者是来自麻省理工学院的博士生邓明扬,这也是他加入何恺明团队后以第一作者身份发表的首篇论文。该研究的核心创新在于,它将生成模型中分布演化的过程从昂贵的“推理阶段”转移到了神经网络的“训练阶段”,从而实现了真正意义上的单步生成(One-step Generation)。
生成模型新范式:漂移模型
漂移模型的核心思想可以概括为两点:
- 将迭代从推理转为训练:不同于扩散模型在生成时需要多次迭代去噪,漂移模型将深度学习固有的“迭代训练过程”本身视为分布演化的驱动力。这样一来,高质量生成在推理时仅需单步即可完成。
- 利用“漂移场”趋向平衡:模型通过引入一个受数据吸引和自身排斥的“漂移场”作为学习目标。当模型的生成分布与真实数据分布完全匹配时,这个漂移场会归零,达到动态平衡,标志着模型学习完成。
理解这一点,我们需要回到生成模型的本质。与判别模型学习样本到标签的映射不同,生成模型的核心是学习一个映射函数 f,将一个简单的先验分布(例如高斯噪声)变换为与真实数据匹配的推移分布。
当前主流的范式,如扩散模型或流匹配模型,将这种分布演变放在了推理阶段进行迭代。这意味着生成一张图片需要调用神经网络成百上千次,计算开销巨大。
漂移模型则提出了一种颠覆性的视角:将分布的演化从推理阶段转移至训练阶段。这一设计的可行性根植于深度学习的本质——神经网络的训练本身就是一个迭代优化的过程(例如随机梯度下降SGD)。
在传统视角下,我们只关心损失函数的下降。但在漂移模型中,训练的每一轮迭代都被赋予了新的物理意义:模型参数的微小更新,会直接驱动其输出样本在特征空间或像素空间中产生位移。论文将这种随训练步数发生的样本位移定义为漂移。
这意味着,映射函数 f 随着参数不断优化,它所产生的推移分布也随之自然地动态演变。模型训练的轨迹,本质上就等价于分布演化的路径。既然训练过程已经完成了演化,推理时自然无需多步迭代。
由此,漂移模型将原本昂贵的迭代开销“内化”在了训练阶段,使得模型在推理时仅需一次前向传播即可生成高质量样本,不仅大幅提升了效率,也避免了GAN对抗训练的不稳定性。
通过漂移场引导样本移动
在具体实现上,论文引入了漂移场来量化并引导这种样本移动,从而控制推移分布的演变。
与流匹配中在推理阶段引导样本移动的向量场不同,漂移场是一个作用于训练阶段的函数,用于刻画样本空间中的演化趋势。给定一个由当前模型生成的样本,漂移场会计算出一个用于修正该样本位置的位移向量 V。
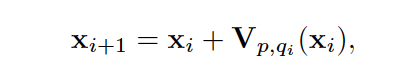
这个位移向量本质上是为神经网络的参数更新提供“导航”。通过在训练迭代中不断最小化这个漂移量,模型被强制在训练完成时就将其输出分布与目标数据分布对齐,从而实现“一出厂就达标”的单步生成。
训练的目标是建立一种平衡:当生成分布与真实数据分布完全匹配时,漂移场处处为零。论文巧妙地将这一更新规则转化为一种基于梯度停止的损失函数。
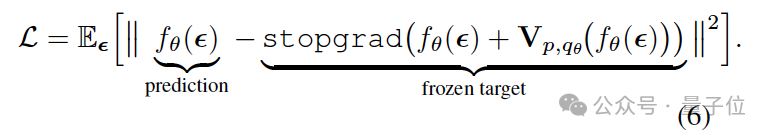
该损失函数并不直接对复杂的漂移场求导,而是将“当前样本位置 + 漂移向量”计算出的位置视为一个冻结的目标,然后驱使模型的预测向这个目标靠拢,从而间接地最小化漂移量。
在算法层面,每个训练步骤可以概括为:
- 生成样本:从先验分布(如高斯分布)采样噪声,通过当前网络生成样本
x。
- 获取参考:从数据集中采样真实样本作为正样本
y+,并从生成分布或其他分布采样作为负样本 y-。
- 计算漂移:根据正、负样本的分布,计算出当前位置
x 的漂移向量 V。
- 优化更新:将
(x + V) 设为目标值(并停止其梯度),然后更新网络参数,使其输出向该目标靠近。
为了处理像图像这样的高维数据,论文还引入了几项关键设计:
- 特征空间映射:不再局限于像素空间,而是利用MAE等预训练自监督模型构建的特征空间。在更高维的语义层面进行分布匹配,显著提升了生成结果的语义保真度。
- 吸引与排斥场:漂移场被具体定义为吸引场和排斥场的结合。生成的样本受到真实数据分布的吸引力以确保细节准确,同时又受到当前生成分布中其他样本的排斥力,以维持样本多样性并防止模式坍缩。
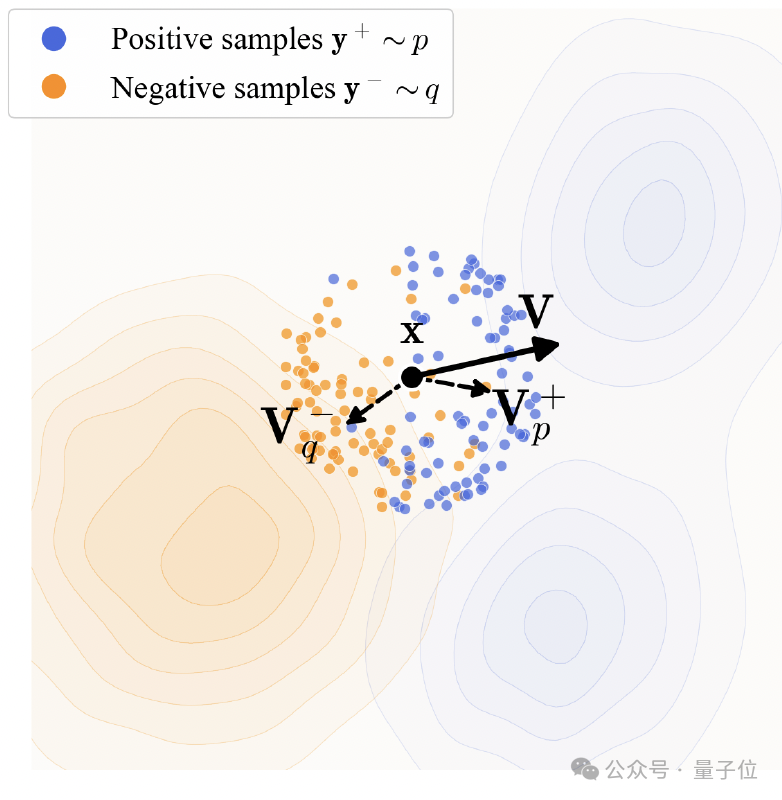
- 核函数与归一化:为了精确稳定地估计这种“力场”,研究引入了指数核函数来衡量样本间的相似度,并借鉴对比学习的思想,通过Softmax进行归一化处理。
- 内置的CFG机制:更巧妙的是,该范式将分类器自由引导机制直接内化于训练阶段。通过在计算漂移时向负样本中混入无条件的真实数据,模型在训练迭代中就自发学会了条件外推。这使得模型在推理时无需额外步骤,单步采样就能获得极强的引导效果。
实验结论
在最具挑战性的ImageNet 256×256基准测试中,漂移模型展现了卓越的性能。
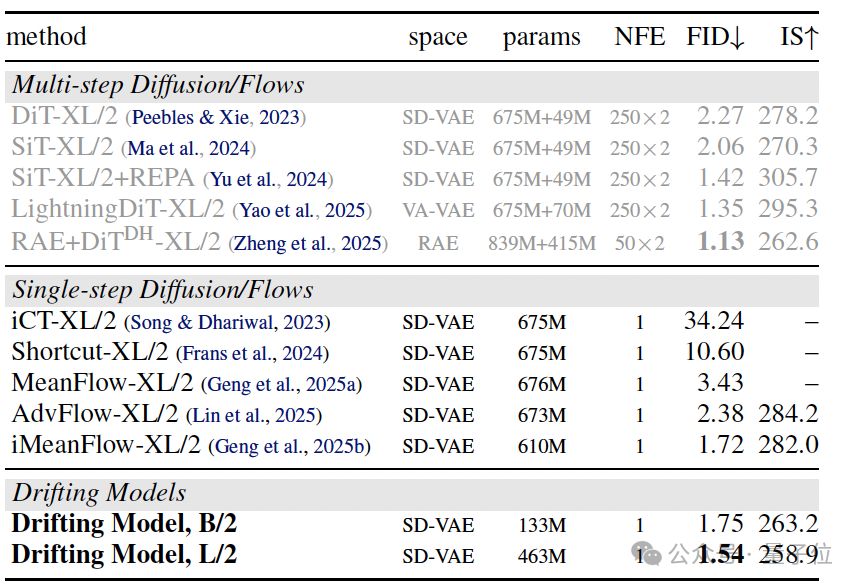
如表所示,漂移模型在单步推理下,于潜空间取得了1.54的FID分数,在像素空间取得了1.61的FID分数。这一成绩不仅刷新了单步生成的纪录,甚至优于许多需要250步迭代推理的传统扩散模型或流匹配模型。
除了图像生成,该范式在机器人控制等序列决策任务中也表现出极强的泛化能力。
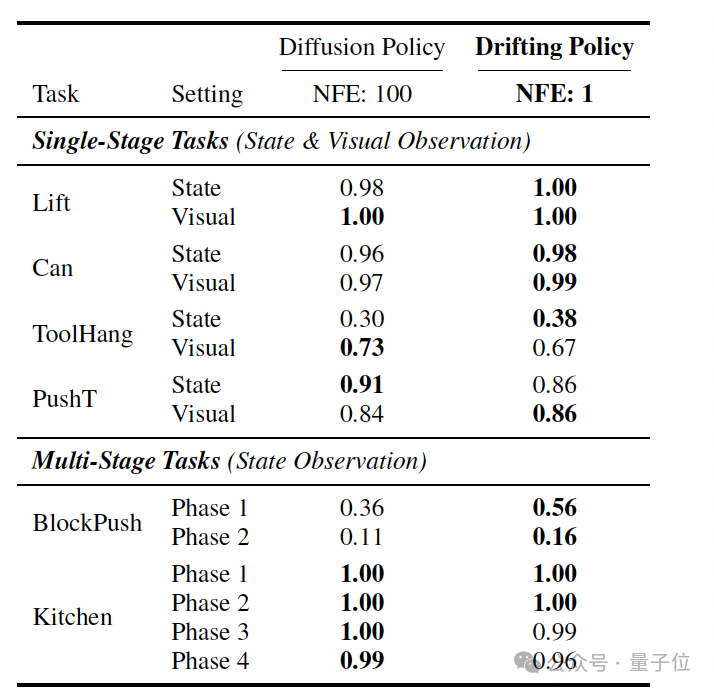
实验表明,采用漂移策略的模型,其单步推理的决策质量即可匹配甚至超越需要100步推理的Diffusion Policy,这为对延迟要求极高的实时控制系统提供了新的可能。
总结来看,漂移模型成功地将生成所需的“迭代压力”从推理阶段转移至训练阶段,实现了真正意义上的“一步到位”。这一工作不仅提供了一种不同于传统SDE/ODE微分方程框架的生成新视角,更将神经网络的训练过程本身,重新诠释为驱动分布演变的动力机制。对于计算机视觉和生成式AI领域的研究者与开发者而言,这无疑开启了一扇值得深入探索的新大门。
论文信息