在数学中,线性代数往往被视为一门“基础而工具化”的学科。然而,当研究从矩阵运算、线性方程组逐步推进到更抽象的结构层面时,一个概念会反复出现,并逐渐显露其深层意义——内积空间。内积空间提供了一套在抽象线性结构中讨论“几何性质”的精密语言,使得距离、正交、投影、最优化等思想能够在高度一般的环境中被严格表述与系统研究。理解内积空间,实际上是在理解一种将代数结构与几何思想进行深度统一的方式;而这一方式,又在分析、概率、数值计算、信号处理等领域持续发挥基础性作用。
1 线性空间为何还不够
在数学结构的层级中,线性空间是最为基础且核心的概念之一。它通过向量加法和标量乘法的封闭性以及满足一系列代数公理,为研究者提供了对向量及其组合关系的形式化描述。通过这些公理,可以定义线性组合、线性相关性、基与维数,进而研究向量空间的维度、子空间及其交并性质。然而,当我们尝试在这种纯代数环境中讨论更几何化的问题时,线性空间的结构表现出显著的局限性。
首先,考虑“向量长度”的概念。在日常几何中,向量长度是测量方向性量的基本工具,它允许比较向量的大小、确定单位向量,并在计算距离时起核心作用。然而,仅是线性空间并没有提供任何测量“大小”的机制。给定任意向量 v,线性空间的公理无法赋予 v 一个数值化的“长度”。因此,讨论两向量间的距离 d(u, v) 或在空间中移动的路径长都缺乏定义基础。
其次,向量间的角度与方向关系在纯线性结构中并没有明确意义。几何直观告诉我们,两个向量可以“垂直”或者形成某种角度,但在纯线性代数中,“垂直”并没有内在定义。我们仅知道向量可以被加起来形成新向量,或可以按比例缩放,但无法判断某种组合是否构成角度意义上的独立方向。换句话说,线性空间无法区分方向上的独立性,只能判断线性相关性,而线性相关性仅反映代数上的依赖,而非几何上的正交性。
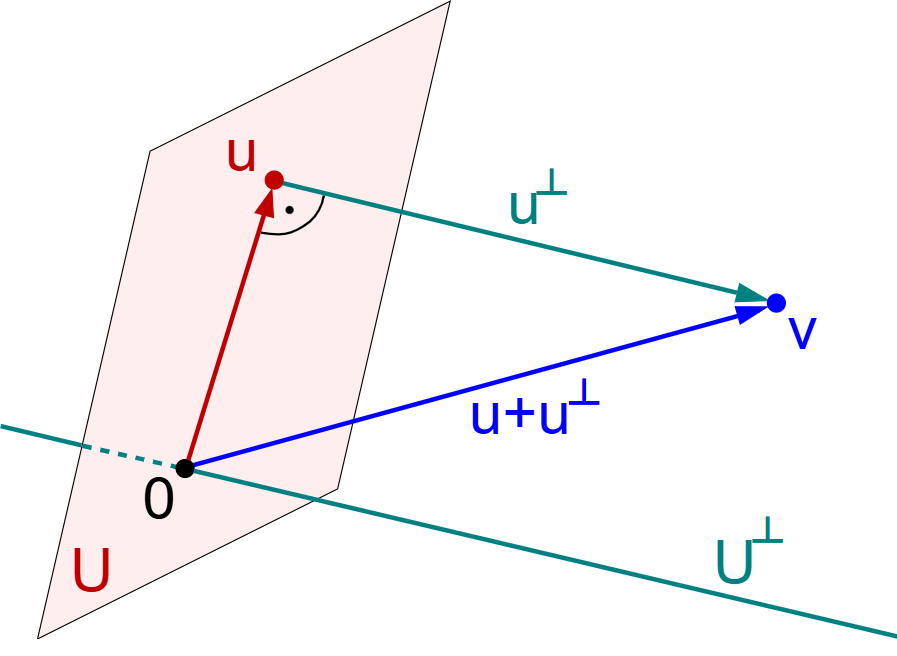
再次,考虑向量在子空间中的投影问题。假设 U 是 V 的子空间,对于向量 v,我们希望定义“在 U 上的分量”。在欧几里得空间中,这一分量是通过垂直投影得到的:v = u + u⊥,其中 u ∈ U,u⊥ ⊥ U。在纯线性空间中,虽然可以找到 U 的某种分解 v = u + w 使得 u ∈ U,w ∈ W,但没有规范方法去选择唯一的分解,也无法定义 u 与 w 的正交性。投影的概念因缺乏“角度”或“垂直”的结构而无法严格定义。
这些问题表明,线性空间在代数操作上足够完备,但在几何解释上明显不足。直观上,我们希望在向量空间中讨论长度、角度、正交性、投影和距离等概念,而这些概念都依赖于一种额外的结构:内积。这种结构不仅提供了长度的度量标准,也赋予向量间相互关系以定量描述,使得代数与几何可以在同一框架下统一。
可以形式化地理解为:在一个线性空间 V 中,若我们定义一个映射
⟨·, ·⟩: V × V → ℝ(或 ℂ)
并赋予它特定的性质(如正定性、线性性与共轭对称性),那么它可以诱导出以下几何概念:
- 长度(范数):
∥v∥ = √⟨v, v⟩
- 距离:
d(u, v) = ∥u - v∥
- 角度与正交性:
cos θ = ⟨u, v⟩ / (∥u∥ ∥v∥),若 ⟨u, v⟩ = 0 则正交
- 投影:在子空间
U 上的正交投影 u 由条件 ⟨v - u, w⟩ = 0 (∀ w ∈ U) 唯一确定。
这些结构在纯线性空间中是无法定义的,因此内积的引入是必然的需求。如果不引入内积,我们无法从代数结构过渡到几何分析,也就无法在向量空间中讨论误差最小化、最优近似、信号分解、傅里叶展开等问题。
再考虑一个具体例子:在二维实线性空间 ℝ² 中,向量 (1, 0) 和 (1, 1) 线性独立,我们可以得到整个空间的基。但在没有内积的情况下,我们无法判断 (1, 0) 与 (1, 1) 是否“垂直”,也无法定义它们的长度。如果我们希望计算 (2, 3) 在 (1, 0) 方向上的分量,或者求 ∥(2, 3)∥,则线性空间的公理无法提供任何指导。只有当定义内积
⟨(x1, y1), (x2, y2)⟩ = x1*x2 + y1*y2
之后,长度、正交与投影才得以严格定义,并与我们直观的几何理解完全一致。
更一般地,在高维或无限维空间中,例如函数空间 L²([a, b]),线性组合和加法依然成立,但没有内积,我们无法讨论函数间的“角度”、“长度”或“最优逼近”。通过定义内积
⟨f, g⟩ = ∫_a^b f(x) g(x) dx
这些概念被严谨地引入,并允许使用正交展开、傅里叶级数等工具进行分析。
因此,总结来看,线性空间提供了代数框架,允许我们讨论组合、相关性、维数等代数性质,但几何性质如长度、角度、正交、投影等依赖于内积结构。没有内积,线性空间是“几何贫瘠”的;有了内积,线性空间便获得了丰富的几何结构,代数与几何得以深度统一。这也解释了为什么在学习和研究中,内积空间是理解线性代数与分析之间连接性的核心概念。
内积的引入不仅仅是增加一种运算,更是一种赋予抽象向量空间以度量和方向感的方法,使得线性空间的元素能够被“量化”与“比较”,从而使投影、正交展开、最优化等分析方法在任意维度上都能严密成立。这正是线性空间在代数层面之上必须扩展到内积空间的根本原因。
2 内积的定义及其数学约束
在对线性空间的局限性进行深入分析后,内积的引入成为自然选择。内积不仅为向量空间提供“几何维度”,还使代数与几何的概念能够在严格的数学框架下统一。因此,理解内积及其数学约束,是掌握内积空间概念的关键步骤。
2.1 内积的公理化定义与基本性质
设 V 是定义在实数域 ℝ 或复数域 ℂ 上的线性空间。内积是一个映射:
⟨·, ·⟩: V × V → 𝔽 (𝔽 = ℝ 或 ℂ)
其中 𝔽 是 ℝ 或 ℂ,使得以下性质成立:
-
共轭对称性(Hermitian symmetry)
⟨u, v⟩ = \overline{⟨v, u⟩}
这一性质保证了在复数空间中,向量间的“相互关系”不会依赖于顺序。换句话说,如果 u 与 v 的关系是某种方向上的度量,那么反向测量得到的是复共轭,保证了模长和角度的合理定义。
-
线性性(第一变量)
⟨αu + βv, w⟩ = α⟨u, w⟩ + β⟨v, w⟩ (∀ α, β ∈ 𝔽, u, v, w ∈ V)
对于实内积空间,线性性是双线性的,而对于复内积空间,通常第一变量满足线性,第二变量满足共轭线性(即 ⟨u, αv + βw⟩ = \bar{α}⟨u, v⟩ + \bar{β}⟨u, w⟩)。线性性保证了向量组合与内积测量之间的协调性,这对于投影、展开以及最小化问题至关重要。
-
正定性(Positive-definiteness)
⟨v, v⟩ ≥ 0, 且 ⟨v, v⟩ = 0 ⇔ v = 0
正定性确保内积可以诱导出一个合理的“长度”度量。对于任意非零向量 v,⟨v, v⟩ 总是严格正数,从而定义的范数 ∥v∥ 保证非负性。
这些公理是经过严格逻辑推敲后得到的最低约束条件,使得内积能够引导出一致的几何结构。若放宽其中任一条件,许多基础概念将失去意义。例如,如果舍弃正定性,则长度可能为负数,投影与最小误差计算将不再具有单调性与唯一性;若摒弃共轭对称性,则在复数空间中角度概念将无法保持稳定;若摒弃线性性,则投影、展开等操作将失去可操作性和代数一致性。
实例:实向量空间 ℝ^n 的标准内积
在 ℝ^n 中,定义内积为:
⟨x, y⟩ = Σ_{i=1}^n x_i y_i
验证公理:
- 共轭对称性:实数域下
⟨x, y⟩ = ⟨y, x⟩
- 线性性:
⟨αx + βy, z⟩ = α⟨x, z⟩ + β⟨y, z⟩
- 正定性:
⟨x, x⟩ = Σ x_i² ≥ 0,且 = 0 ⇔ x = 0
这个例子显示了内积公理在最常见的欧几里得空间中成立,也是内积理论的直观来源。
2.2 内积的几何意义与条件的不可替代性
内积不仅提供一种双线性映射,更是一种几何工具:
-
长度与距离由内积定义的范数:
∥v∥ = √⟨v, v⟩
为向量赋予数值化大小,使得距离:
d(u, v) = ∥u - v∥ = √⟨u-v, u-v⟩
成为有效度量。
-
正交性与角度若 ⟨u, v⟩ = 0,则称 u 与 v 正交。更一般地,可定义角度:
cos θ = ⟨u, v⟩ / (∥u∥ ∥v∥)
在实内积空间中为标准余弦公式,在复内积空间中考虑实部以保证几何解释合理。
-
投影与最小化设 U 是子空间,向量 v 的正交投影 u 满足:
u ∈ U, 且 ⟨v - u, w⟩ = 0 (∀ w ∈ U)
投影向量是 v 在 U 上的最佳近似:
∥v - u∥ ≤ ∥v - w∥ (∀ w ∈ U)
这里最小化性质完全依赖于内积定义,它保证误差度量的合理性。
条件不可随意删改的分析
- 若缺乏正定性:
⟨v, v⟩ 可能为负,范数无法定义,距离不再具有度量意义,投影最小化失效。
- 若缺乏共轭对称性:在复数空间中,
⟨u, v⟩ ≠ \overline{⟨v, u⟩},导致角度不对称,几何解释矛盾。
- 若缺乏线性性:向量组合的内积无法被拆解,正交投影公式、最小二乘法推导、傅里叶展开等运算将失效。
因此,内积公理不仅定义了一类函数,更是内积空间几何与分析工具的基石。它的三个核心条件相互补充,保证了从代数运算到几何解释再到分析应用的完整闭合性。
2.3 内积与柯西–施瓦茨不等式的联系
内积定义后,一个立即可得的重要结论是柯西–施瓦茨不等式:
|⟨u, v⟩| ≤ ∥u∥ ∥v∥
这一不等式不仅是内积空间的基础工具,还确保角度和距离概念的稳定性。它保证内积不会“过大”,使得向量间的关系不会超过几何直觉允许的范围。在应用中,这一结果用于证明三角不等式、最小二乘解唯一性、正交展开收敛性等关键结论。
证明略示意如下:对任意 λ ∈ ℝ 或 ℂ,考虑向量 u - λv 的范数:
0 ≤ ∥u - λv∥² = ⟨u - λv, u - λv⟩ = ∥u∥² - 2Re(λ⟨u, v⟩) + |λ|²∥v∥²
通过选择最优 λ,即可得到:
|⟨u, v⟩|² ≤ ∥u∥² ∥v∥²
即柯西–施瓦茨不等式。
这一推导显示了内积条件与几何性质之间的紧密联系:线性性允许展开,正定性保证非负性,共轭对称性保证复数情况下取模正确。
3 从内积到范数与距离
3.1 范数的诱导
一旦内积被给定,就可以定义范数:∥v∥ = √⟨v, v⟩。
这一范数满足非负性、齐次性和三角不等式。后者依赖于一个关键结果——柯西–施瓦茨不等式:|⟨u, v⟩| ≤ ∥u∥ ∥v∥。
这一不等式不仅是内积空间理论的核心结论之一,也在统计、概率与数值分析中反复出现。它保证了内积不会“过大”,从而使角度与距离的概念具有稳定意义。
3.2 距离结构的出现
由范数进一步定义距离:d(u, v) = ∥u - v∥。
于是,一个内积空间成为一个度量空间。这一结果意味着极限、连续性、收敛性等分析概念可以被引入到线性代数环境中。这也是为何在函数空间研究中,内积空间常常被视为分析与代数之间的重要接口。
4 正交性与几何结构
4.1 正交的定义与含义
在内积空间中,两个向量 u, v 若满足 ⟨u, v⟩ = 0,则称它们正交。正交性是一种通过内积严格定义的关系。它描述了向量之间在结构层面上的“独立方向性”。
4.2 正交基与结构简化
若一个基由两两正交的单位向量组成,则称为正交规范基。这样的基使得向量的坐标表示与内积运算极为简洁:若 v = Σ α_i e_i, u = Σ β_i e_i,则 ⟨u, v⟩ = Σ α_i \bar{β_i}。
在此背景下,许多计算问题可以被拆解为分量级别的独立问题。这种结构上的简化是内积空间几何特性带来的直接结果。
5 投影、最小化与近似思想
5.1 正交投影的定义
设 U 是内积空间 V 的一个子空间。对于任意 v ∈ V,有唯一的分解:v = u + w,其中 u ∈ U,w ∈ U⊥。
向量 u 被称为 v 在 U 上的正交投影。这个结论不仅具有形式上的美感,更为最小二乘法等方法提供了理论依据。
5.2 最优近似的内在解释
正交投影满足如下性质:∥v - u∥ = min_{w ∈ U} ∥v - w∥。
这说明投影是在所有可能近似中给出误差最小的选择。这里并未使用任何额外假设,仅依赖内积结构本身。这一思想在函数逼近、数据拟合等问题中具有广泛影响。
6 复内积空间与实内积空间的差异
6.1 共轭结构的重要性
在复数域上,若仍采用完全对称的双线性形式,则正定性将无法保持。因此,共轭对称性的引入是结构稳定性的必要条件。
6.2 相位因素的影响
在复内积空间中,⟨u, v⟩ 本身是复数,其模长与相位分别携带不同信息。模长与“相似程度”相关,而相位则反映更细致的结构关系。这一特性使得复内积空间在信号分析、量子理论等方向具有不可替代的表达能力。
7 内积空间与线性算子的关系
7.1 伴随算子的定义
给定线性算子 T: V → V,若有算子 T* 使得⟨Tu, v⟩ = ⟨u, T*v⟩, 则称 T* 为 T 的伴随算子。
7.2 自伴随算子与谱结构
自伴随算子满足 T = T*。这类算子具有实特征值、正交特征向量等重要性质,使得复杂算子可以在适当基下被对角化。此类结果构成算子理论的重要内容。
8 结语
在基础线性代数中,内积常常被介绍为点积的推广。然而,从更高层次看,内积空间的真正价值在于:它为线性结构提供了一种可度量、可比较、可优化的方式,使得代数操作与分析思想在同一框架中协同工作。这种统一性,正是内积空间在现代数学中反复被使用的根本原因。若你对这类深入探讨数学结构与算法思想的话题感兴趣,欢迎持续关注云栈社区。