在现代数学结构、数值体系与高维数据处理框架的讨论中,任何复杂系统只要涉及线性运算,其背后往往便有一段关于分解方法的历史。无论是在科学计算、工程仿真、数据分析、优化算法、信号建模,还是在大型模型训练与数值求解任务中,矩阵分解都提供了一种将复杂结构重新组织的方式,使研究者能够在清晰、可调控、便于推断的框架中探索高维线性映射的内部逻辑。
当维度增长、参数耦合加深、误差随计算路径逐步累积时,直接处理一个复杂矩阵往往变得困难。其参数并非孤立,而是通过结构化关系共同作用,这种耦合关系使高维问题常常失去直观表达。矩阵分解的核心价值便是在维持整体信息的前提下,将矩阵拆解为若干结构良好的成分,使不同成分之间的角色更加分明,使研究者能够从结构规律中分析其行为。
在诸多分解方法中,LU、QR 与 SVD 是最具代表性的三类:LU 对线性系统求解提供了一条高效路径;QR 在正交化、最小二乘、稳定化计算等诸多问题中保持核心功能;SVD 则提供了最完备的结构表达,使任何矩阵的几何作用逻辑都能被清晰描述。它们不仅是计算技术,更是理解线性映射本质的关键工具。
这些方法的价值并不局限于“拆分矩阵”这一表层功能,而在于它们为研究者提供了一种分析框架,使得复杂问题得以转化为结构化问题。例如:LU 让线性系统解算从高维混合计算变为层次化处理;QR 通过正交结构控制误差,使最小二乘问题的结果更加可靠;SVD 则揭示了矩阵内部的尺度方向,使得数据在高维空间的主要规律得以突出,从而形成有效降维、压缩与结构分析路径。
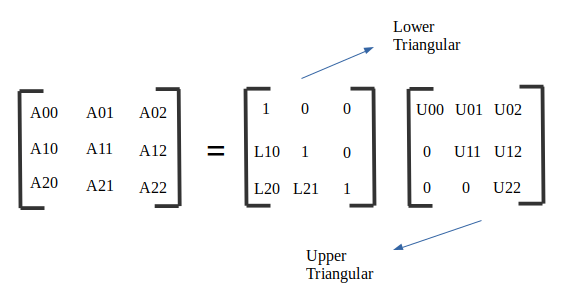
1 矩阵分解在数学体系中的角色
矩阵分解作为线性体系中的关键方法,其价值不仅在于提供一种便于推断的结构表示,更在于通过结构化方式重写原始映射,使研究者能够以更具解析性与更可调控制的形式处理高维问题。
无论研究线性系统求解、最小二乘分析、特征结构、数据降维、算子稳定性,还是研究模型的尺度方向与子空间构造,矩阵分解都为这些主题提供了可解释的基础框架。从抽象数学角度看,它们是一类将矩阵向更规则、结构更明确方向映射的“结构化算子”。从工程与数值角度看,它们是高维问题在有限精度环境中仍可计算、可预期的关键原因。
1.1 将矩阵还原为更易处理的构成元素
许多高维矩阵本身不具备友好结构,其内部参数可能呈现耦合状态,难以直接从原始形式中提取其几何意义、稳定性性质或子空间结构。矩阵分解的核心任务,便是将矩阵拆解为一系列具有明显可处理特征的成分,使得后续分析能够借助更明确的构造进行。
1.1.1 LU、QR、SVD 的结构作用
- LU 分解将矩阵拆成下三角矩阵与上三角矩阵,使线性系统求解可以分为前代与回代两步完成。 例如:若 $A = LU$ ,则求解 $Ax = b$ 等价于逐步求解 $Ly = b$ 与 $Ux = y$,三角结构保证其计算路径具备极高效率与低复杂度。
- QR 分解将矩阵写成正交矩阵与上三角矩阵的乘积,即 $A = QR$,其中 $Q$ 满足 $Q^T Q = I$。 正交结构提升几乎所有相关算法的稳定性,是最小二乘与特征值算法的核心方法。
- SVD将矩阵剖分为旋转—尺度伸缩—旋转的组合:$A = U \Sigma V^T$,其中 $\Sigma$ 的对角值决定矩阵的尺度方向, $U$ 与 $V$ 提供了输入与输出空间的正交基表示。
这三类分解实际上构成了线性代数体系的“结构语言”,使研究者能够以统一方式讨论矩阵的作用规律。
1.1.2 线性映射的几何结构:以 SVD 为代表
线性映射的几何意义往往需要通过坐标变换才能显现。例如 SVD $A = U \Sigma V^T$:
- $V^T$ 将输入向量旋转至奇异值方向;
- $\Sigma$ 决定各方向伸缩程度;
- $U$ 再将伸缩后的向量映射至输出正交基。
因此 $A$ 的几何作用可概括为:
向量$V^T$旋转$\Sigma$伸缩$U$旋转
该解释使高维线性映射的作用具备可视化逻辑:矩阵的影响可以分为几个彼此独立的几何步骤,从而使研究者能够分析其方向、尺度与稳定性。
SVD 的这一性质不仅在理论中常用,也服务于 PCA 分析、矩阵压缩、数据降维、系统辨识、信号滤波等大量工程任务。在现代AI和机器学习中,它更是理解数据结构和设计高效算法的基石。
1.2 计算可行性的基础:降低复杂度
若直接对矩阵应用高维运算,运算成本往往过高。例如直接求解线性系统的复杂度通常是 $O(n^3)$,在大规模问题中难以接受。而通过分解可大幅度减少计算量,提高处理效率。
1.2.1 LU 分解降低求解线性系统的复杂度
LU 分解允许一次分解、多次重复使用。在许多工程场景中,需要求解如下多右端问题:
$A x_1 = b_1, \quad A x_2 = b_2, \quad \dots$
若使用 LU 分解 $A = LU$,则只需一次分解,重复执行三角求解即可,每次仅成本 $O(n^2)$。因此在需要大量求解的结构化问题中,LU 是速度最优的选择之一。
1.2.2 QR 分解使最小二乘问题更高效
最小二乘问题:
$\min_x \|Ax - b\|_2$
若直接形成 $A^T A$,会导致病态程度增强。而利用 QR 分解 $A = QR$:
$A^T A x = A^T b \Rightarrow R^T Q^T Q R x = R^T Q^T b$
可化为:
$R x = Q^T b$
该流程避免了平方矩阵 $A^T A$ 的形成,使问题保持稳定且高效。这类优化技术在基于Python的数据分析和科学计算项目中尤为常见。
1.2.3 SVD 的低秩近似提升效率
在大多数数据集、中高维信号与图像问题中,矩阵通常具备低秩规律。若将矩阵写为:
$A_r = U_r \Sigma_r V_r^T$
则当 $r$ 远小于原始维度时,矩阵压缩比与运行速度都会显著提升。
因此,SVD 常常被用于:
- 压缩大规模矩阵;
- 构建低维模型;
- 提供高效特征提取方法;
- 减少计算量与存储成本。
1.3 数值稳定性的核心来源:正交结构
在高维数值计算场景中,误差累积往往是影响结果可靠性的关键因素。而正交结构使计算中的误差不会被放大,因此构成了许多稳定化算法的基础。
1.3.1 正交矩阵保持向量长度
若 $Q$ 为正交矩阵,则:
$\|Qx\|_2 = \|x\|_2$
这意味着:
- 正交矩阵不放大初始误差;
- 数据在映射后保持尺度一致;
- 迭代算法中误差不会指数级累积。
1.3.2 QR 与 SVD 在浮点环境中的优势
在浮点计算中,数值条件差的矩阵会导致严重误差放大。QR 与 SVD 使用的正交结构使得相关算法更具优势:
- QR 分解经常被用于最小二乘、正交投影、稳定滤波;
- SVD 用于判断矩阵是否病态,并给出误差敏感方向;
- 特征值算法依赖 QR 迭代保证稳定收敛。
在工程实践中,正交结构通常意味着更可靠的数值表现。
2 LU 分解:方程求解与结构化分析的基础工具
LU 分解是求解线性系统的核心方法之一,通过将矩阵拆成下三角矩阵 $L$ 与上三角矩阵 $U$,使复杂的消元操作变为明确的层次结构。
从数学体系看,LU 提供了矩阵的结构化表达,使线性系统求解、矩阵逆推演、数值算法的构造均变得可管理。从工程体系看,LU 的高效性使其成为大型科学计算与矩阵库实现的标准路径。
2.1 LU 分解的基本形式
一个满秩且满足适当条件的矩阵 $A$,可以写成:
$A = LU$
其中:
- $L$ 为下三角矩阵(对角线为 1 或其他约定值);
- $U$ 为上三角矩阵。
这意味着 $A$ 的作用被分成两步:
- 下三角矩阵 $L$ 的前代过程;
- 上三角矩阵 $U$ 的回代过程。
以此便能在 $O(n^2)$ 内求解任意线性系统 $Ax=b$。
2.1.1 LU 的代数构造逻辑
LU 分解本质上是高斯消元的矩阵形式表达。若高斯消元将矩阵写为:
$E_{n-1} \dots E_2 E_1 A = U$
其中每个 $E_k$ 为消元矩阵,则:
$A = (E_1^{-1} E_2^{-1} \dots E_{n-1}^{-1}) U$
定义:
$L = E_1^{-1} E_2^{-1} \dots E_{n-1}^{-1}$
即可得到 $A = LU$。
因此 LU 分解的背后,是高斯消元将原始矩阵重写为易处理结构的过程。
2.2 LU 分解为何是方程求解的核心方法?
在工程环境中,求解线性系统往往是最常见、最基础、最依赖效率的任务。LU 之所以成为核心方法,原因在于:
2.2.1 可重复使用性强
假设要解多个系统:
$A x_1 = b_1, \quad A x_2 = b_2, \quad \dots$
只需一次 LU 分解 $A = LU$,而后执行多次三角求解即可,整体效率大幅提高。
2.2.2 结构友好,易于存储与分块
三角矩阵的存储结构简单,与现代 CPU 缓存、并行计算策略高度契合。许多矩阵库(如 LAPACK)都针对 LU 进行了深度优化。
2.2.3 便于构造逆矩阵(尽管工程中通常避免直接计算逆)
若需要构造逆矩阵 $A^{-1}$,则每列都可通过三角求解获得:
$A X = I$
其中 $X = A^{-1}$。这同样依赖 LU 的重复利用特性。
2.3 LU 分解的数值稳定性问题与主元策略
相比 QR 与 SVD,LU 的数值稳定性不完全理想,因此在实际使用中通常采用主元策略。
2.3.1 部分主元策略
通过对矩阵做置换,使得:
$PA = LU$
其中 $P$ 为置换矩阵,用于选择更大主元,避免误差放大。
主元策略可显著增强数值鲁棒性,使 LU 分解成为可在工程环境安全使用的方法。
2.3.2 完全主元策略
完全主元策略允许选取最大绝对值作为主元,但成本更高,工程上较少使用。多数高性能库采用部分主元策略即可获得足够稳定性。
2.3.3 与 QR、SVD 的稳定性对比
- LU:速度最快,但稳定性依赖主元策略
- QR:稳定性明显优于 LU
- SVD:最稳定,但成本最高
因此在实际应用中:
- 需要最大稳定性 → 使用 SVD
- 需要稳定与效率平衡 → 使用 QR
- 需要最高效率且问题允许 → 使用 LU
3 QR 分解:正交化、最小二乘、稳定算法的核心
3.1 QR 分解的结构
QR 分解将矩阵写为:
$A = QR$
其中 $Q$ 为正交矩阵, $R$ 为上三角矩阵。
QR 分解的核心用途:
- 最小二乘问题;
- 正交化;
- 求特征值的 QR 迭代;
- 稳定的列空间分析。
3.2 为什么 QR 比 LU 稳定?
原因在于正交矩阵具有优异的浮点性质:
因此在许多情境中,QR 是数值稳定化处理的必要结构。
3.2.1 最小二乘问题中的应用
最小二乘问题:
$\min_x \|Ax - b\|_2$
若直接计算 $A^T A$ 会导致严重的病态增幅,而 QR 分解允许直接进行:
$A = QR \Rightarrow \|QRx - b\|_2 = \|Rx - Q^T b\|_2$
此路径稳定且高效,是工程标准做法。
3.3 QR 分解与特征值计算
QR 迭代算法是矩阵特征值计算的核心步骤。其结构如下:
- 将矩阵写为 $A_0 = A$
- 迭代:
$A_k = Q_k R_k$
$A_{k+1} = R_k Q_k$
其中 $A_k = Q_k R_k$ 为其 QR 分解。
该迭代过程能够在保证稳定性的同时提取特征值,是现代 LAPACK 库与大型科学计算平台的主算法。
4 SVD:最强结构化分解与数据科学核心标准
4.1 SVD 的定义
矩阵 $A$ 的奇异值分解:
$A = U \Sigma V^T$
其中:
- $\Sigma$ 为非负奇异值构成的对角矩阵;
- $U$ 与 $V$ 为正交矩阵。
SVD 是所有分解中结构最完整、性质最优良的。
4.2 SVD 的低秩近似能力
在信号处理、图像压缩、数据降维中最常用的结构是:
$A_r = \sum_{i=1}^{r} \sigma_i u_i v_i^T$
这里 $r$ 为秩限制。
该近似是所有矩阵近似中误差最小的(Frobenius 范数意义下)。 正因如此,SVD 在 PCA、推荐系统、矩阵压缩中占据中心位置,是处理高维数据不可或缺的工具,其思想也深刻影响了现代机器学习模型的设计。
4.3 SVD 的几何意义
其几何意义如下:
- $V$ 的列构成输入空间的正交基;
- $U$ 的列构成输出空间的正交基;
- $\Sigma$ 的对角值是伸缩比例。
因此矩阵的整个结构被重写为“旋转—伸缩—旋转”的组合。
4.4 SVD 与机器学习中的结构
SVD 在数据科学中的应用:
- PCA(对协方差矩阵进行 SVD)
- 噪声抑制(低秩部分保留主要结构)
- 推荐算法(矩阵分解)
- 文本分析(LSA 使用 SVD)
这些应用背后的共同逻辑: 高维数据常常具备某种低维规律,而 SVD 能有效抽取这些规律。
5 分解方法的数值稳定与工程价值
5.1 浮点计算为何必需分解?
浮点误差不可避免,而分解的结构提供了可调控的误差传播路径:
- 正交矩阵的稳定性使得 QR 与 SVD 成为稳健选择;
- LU 分解通过主元策略减少误差累积;
- 分解结构使得矩阵运算不再直接依赖全部元素,而是依赖更具结构的构成部分。
5.2 条件数分析与矩阵分解
条件数反映矩阵对误差的敏感性。 通过 SVD 可得到矩阵的最重要指标:
$\text{cond}(A) = \frac{\sigma_{\max}}{\sigma_{\min}}$
条件数越大,矩阵越接近病态。 工程分析常常需要判断矩阵是否可用于可靠计算,而 SVD 是检测病态程度的核心路径。
5.3 分解实现高维问题的可操作性
在超大规模矩阵场景中(例如稀疏矩阵、核矩阵、图拉普拉斯矩阵),直接计算往往不现实。 分解技术使得:
- 稀疏结构得以保持;
- 子空间投影得以高效实现;
- 算法可分块执行;
- 能有效利用高性能计算环境。
这些特征保证了分解技术在实际工程中的重要位置。
6 结语
矩阵分解(LU、QR、SVD)作为线性代数体系的三类核心技术,覆盖计算、几何解释、数据分析、数值稳定性、信号处理、模型压缩等多个方向。
LU 提供了最基础的高效方程求解路径;QR 提供了稳健的正交化与最小二乘计算结构;SVD 则以最完整的结构解析能力支撑高维数据分析。
它们的重要性不仅体现在算法功能,更体现在它们所揭示的矩阵深层结构,使得原本难以处理的高维问题重新获得可分析、可计算、可理解的形式。 因此在数学、工程、科学、数据处理领域,矩阵分解长期保持其关键位置,并将在数据规模持续扩大的未来继续发挥其不可替代的功能。