Transformer旋转位置编码RoPE原理与实战：从数学推导到LLaMA源码解析

旋转位置编码RoPE（Rotary Position Embedding）是Transformer模型中的一种创新位置编码策略，已广泛应用于LLaMA、ChatGLM等主流大模型。本文将从实现步骤、源码分析到数学原理进行全面解析，帮助读者深入理解这一关键技术。

位置编码基础概念

由于Transformer的Self Attention机制具有排列不变性，模型无法感知输入序列中单词的位置信息。为了解决这个问题，需要引入位置编码让模型理解词序关系。

位置编码主要分为两大类：

绝对位置编码：根据单个token的绝对位置定义编码，每个位置分配独立的位置向量。实现方式又分为：

• 固定式：如原生Transformer的sin-cos三角函数编码，通过固定公式计算
• 可学习式：如BERT和GPT，通过训练自适应学习位置向量

相对位置编码：对两个token之间的相对位置进行建模，将相对位置信息注入Self Attention结构中，代表模型包括Transformer-XL和DeBERTa。

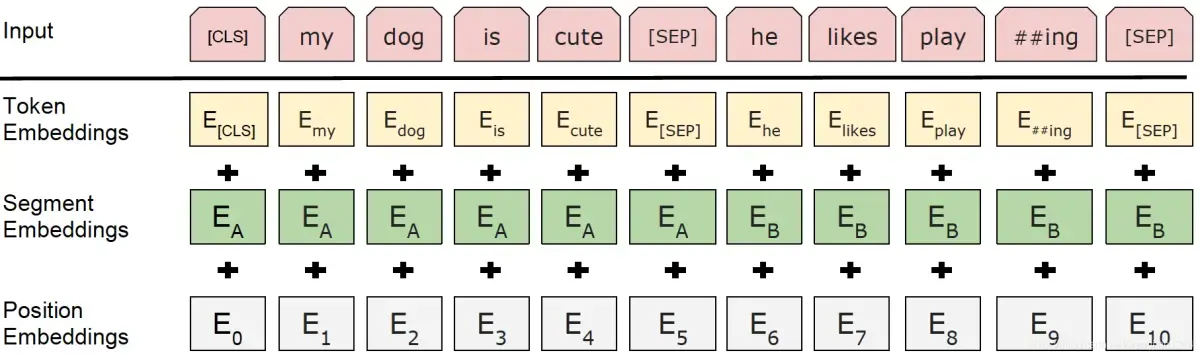
RoPE的本质与计算流程

旋转位置编码RoPE是一种固定式的绝对位置编码策略，但其巧妙之处在于：通过绝对位置编码的实现方式，配合Attention内积机制，最终达到相对位置编码的效果。

RoPE的核心思想是对Query和Key向量进行变换，使变换后的向量自动携带位置信息，而无需修改Attention的内积结构。这种设计既保持了实现的简洁性，又兼具了相对位置编码的优势。

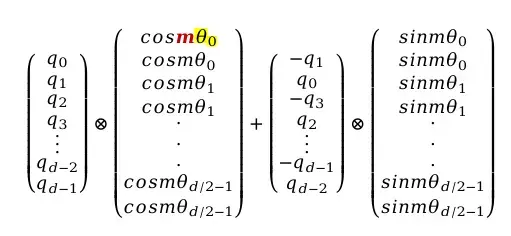
RoPE的计算公式如下：

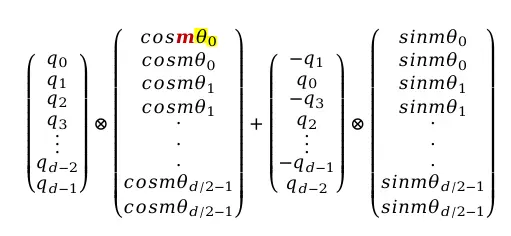
公式解读：

• 第一项：位置为m的token的原始Query向量
• 第二项：包含cos三角函数的向量，与Query逐位相乘
• 第三项：由原始Query变换而来
• 第四项：包含sin三角函数的向量

位置信息由参数m和θ共同表征，其中m为token在句子中的位置，θ与向量各元素位置相关：

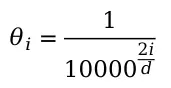
计算示例

以"我爱你"中的第二个词"爱"为例，假设词向量维度d=4，向量表征为[0.2, 0.1, -0.3, 0.7]，RoPE变换的计算过程如下：

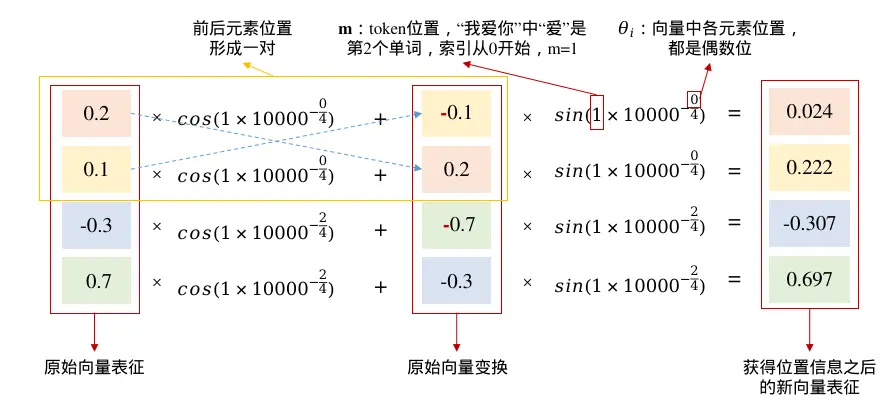
公式中的第三项由原始向量变换而来，将前后两个元素位置构成一对，交换位置并对偶数位取相反数。每个元素位的位置信息注入，可以看作该元素和其相邻元素分别经过sin、cos三角函数加权求和的结果。

RoPE如何表达相对位置信息

RoPE与传统sin-cos位置编码的对比：

实现途径不同：

• sin-cos编码：三角函数性质天然具备表达相对距离的能力
• RoPE编码：本身不能表达相对距离，需结合Attention内积激发相对位置表达能力

融合方式不同：

• sin-cos编码：直接与原始输入相加
• RoPE编码：采用类似哈达马积的相乘形式

RoPE的关键特性：带有RoPE位置编码的两个token，其Query向量和Key向量进入Self Attention后，内积结果可以恒等转化为一个函数，该函数仅与Query向量、Key向量以及两个token位置之差相关。这使得RoPE在不改变Attention结构的前提下，实现了相对位置信息的感知。

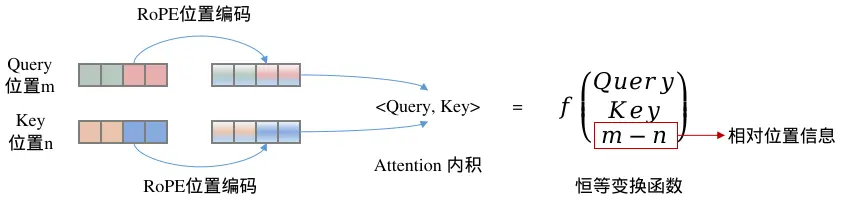
LLaMA源码实现解析

在HuggingFace的LLaMA大模型实现中，RoPE的计算分为三个步骤：

步骤一：初始化cos向量和sin向量

根据上下文窗口大小m和每个头的向量维度d，生成cos和sin向量。在LLaMA2中，上下文窗口m=4096，每个头的向量维度d=128。

class LlamaRotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
        super().__init__()
        # dim=128, max_position_embeddings=4096
        inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
        self.register_buffer("inv_freq", inv_freq)

        self.max_seq_len_cached = max_position_embeddings
        # 生成位置索引 [0, 1, 2, ..., 4095]
        t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device, dtype=self.inv_freq.dtype)
        # 笛卡尔积生成mθ组合矩阵
        freqs = torch.einsum("i,j->ij", t, self.inv_freq)
        # [4096, 64] => [4096, 128]
        emb = torch.cat((freqs, freqs), dim=-1)
        # [1, 1, 4096, 128]
        self.register_buffer("cos_cached", emb.cos()[None, None, :, :], persistent=False)
        self.register_buffer("sin_cached", emb.sin()[None, None, :, :], persistent=False)

通过m向量和θ向量的笛卡尔积构造mθ组合矩阵，最终形成[4096, 128]的二维矩阵，再转换为四维以匹配多头注意力中Query和Key的形状[batch_size, num_heads, seq_len, head_dim]。

步骤二：截取对应长度的向量

根据输入Query的实际长度截取cos和sin向量。例如上下文窗口为4096，但实际输入句子长度仅为10，则截取前10个位置的向量。

def forward(self, x, seq_len=None):
    return (
        self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
        self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
    )

步骤三：改造Query和Key

使用cos和sin向量，根据RoPE公式对原始Query和Key进行变换：

def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

def rotate_half(x):
    """旋转向量的一半维度"""
    # 前半部分
    x1 = x[..., : x.shape[-1] // 2]
    # 后半部分
    x2 = x[..., x.shape[-1] // 2 :]
    # 后半部分取负号，与前半部分拼接
    return torch.cat((-x2, x1), dim=-1)

值得注意的是，HuggingFace的实现与论文公式在元素配对方式上有所不同：

• 论文公式：q0与q1配对
• 代码实现：q0与q64配对（前半部分与后半部分配对）

这两种方式在数学上是等价的，因为RoPE本质是以元素对为单位进行旋转变换，只要配对策略不重复且维度为偶数，Attention内积都能感知相对位置信息。

在完成Query和Key的改造后，直接输入标准的Attention结构：

attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.head_dim)
attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype)
attn_output = torch.matmul(attn_weights, value_states)

注意：Attention结构无需任何修改，且Value向量不参与RoPE变换。

数学原理推导

RoPE的数学推导涉及复数运算、欧拉公式和旋转矩阵等概念。

推导目标

设位置m的token1的Query为q，位置n的token2的Key为k，改造函数为f，目标是找到一个改造函数，使得：

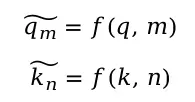
并且Attention内积能够恒等转化为：

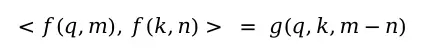
二维情况推导

从最简单的二维向量入手，将q和k用复数表示（第一维为实部，第二维为虚部）。两者的内积等于q和k的共轭复数相乘的实部：

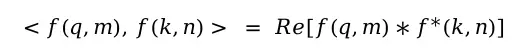
将三个复数用三角形式表示：

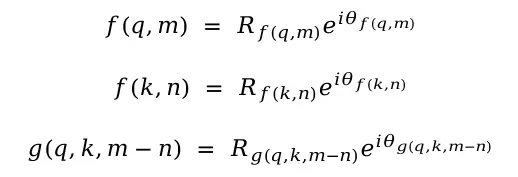
其中R代表向量模长，根据欧拉公式：

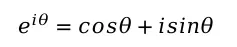
根据复数相乘的性质（模长相乘，幅角相加），可得：

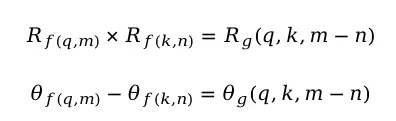
取特例m=n=0，得到：

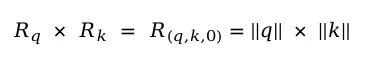
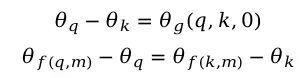
可得θ是关于位置参数m的等差数列函数。将求解的R和θ代入，得到f的一般形式：

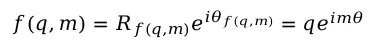
根据欧拉公式展开，该变换对应向量的旋转操作，改写成矩阵形式：

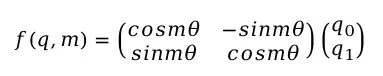
旋转矩阵验证

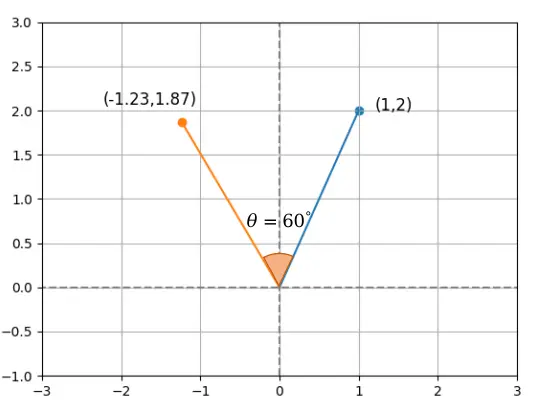
以二维向量[1, 2]旋转60度为例：

import numpy as np

def rotary_matrix(xita):
    matrix = np.array([[np.cos(xita), -np.sin(xita)],
                       [np.sin(xita), np.cos(xita)]])
    return matrix

m = rotary_matrix(np.pi / 3)
one = np.array([[1], [2]])
two = np.matmul(m, one)
print(two)
# array([[-1.23205081],
#        [ 1.8660254 ]])

验证模长不变：

np.linalg.norm(one)  # 2.236
np.linalg.norm(two)  # 2.236

验证旋转角度为60度：

np.dot(one.T, two) / (np.linalg.norm(one) * np.linalg.norm(two))
# array([[0.5]])  # cos(60°) = 0.5

推广到任意偶数维

由于内积满足线性叠加性，任意偶数维向量都可以表示为多个二维情形的拼接，因此RoPE的最终公式为：

从旋转矩阵的角度理解：RoPE本质上是对各个位置的token向量根据自身位置m计算旋转角度，在Attention的内积操作中，内积能够感知旋转后两个向量之间的夹角，这个夹角就是相对位置信息。

总结

旋转位置编码RoPE通过巧妙的数学设计，实现了以下优势：

1. 高效性：无需额外可学习参数，计算开销小
2. 兼容性：无需修改Attention结构，易于集成
3. 表达力：通过绝对位置编码实现相对位置感知
4. 可扩展性：支持任意偶数维度的向量

这些特性使得RoPE成为当前大模型位置编码的主流选择，在LLaMA、ChatGLM等模型中得到广泛应用。理解RoPE的原理和实现，对于深入掌握Transformer架构和大模型技术具有重要意义。

转自 CSDN 作者 AI大模型datian