CUDA编程实战：详解线程全局索引的计算方法与公式推导

在CUDA编程和代码阅读过程中，计算偏移坐标（offset）或全局索引（Global Index）是一项频繁遇到的核心任务。这种计算至关重要，因为它建立了线性内存数据结构与并行计算线程之间的精确映射关系。CUDA通过分层、三维的线程组织模型（Grid, Block, Thread）来实现这种高效的映射，其核心涉及四个内置变量：gridDim、blockDim、blockIdx和threadIdx。

本文将深入解析CUDA的线程组织方式，并详细介绍如何计算线程的全局索引。内容包括：在使用三维网格（3D Grid）和三维线程块（3D Block）时，如何进行全局坐标计算；以及解释当数据指针（如 *src）传递给CUDA核函数（kernel）后，各个线程如何依据计算出的全局索引，准确无误地访问其对应的数据元素。

本文主要内容包括：

1. 线程组织核心概念
2. 全局索引计算公式推导
3. 多种维度组合的示例代码

Part 1: 线程组织核心概念

在CUDA的编程模型中，使用Grid（网格）和Block（线程块）作为线程组织的两级单位。一个Grid包含多个Block，一个Block包含多个Thread（线程）。

相关内置变量为：

• gridDim: 表示Grid中Block的数量维度，类型为dim3。
• blockDim: 表示一个Block中Thread的数量维度，类型为dim3。
• blockIdx: 表示当前Block在Grid中的索引，类型为dim3。
• threadIdx：表示当前Thread在其所在Block中的索引，类型为dim3。

gridDim规定了Block的分布形状，blockDim规定了Thread在Block内的分布形状。这些变量在核函数内部可以直接访问。我们在启动核函数（kernel launch）时，就需要指定Grid和Block的维度，示例如下：

__global__ void kernel(float *src){
   //do something
}
// 定义Grid和Block的形状：
dim3 BlocksPerGrid(N, N, N);  // gridDim 对应 gridDim.x、gridDim.y、gridDim.z
dim3 threadsPerBlock(M, M, M);  // blockDim 对应 blockDim.x、blockDim.y、blockDim.z
// 调用核函数：
kernel<<<BlocksPerGrid, threadsPerBlock>>>(*src);

下图给出了一个具体的示例，其中 gridDim.x=2, .y=2, .z=3； blockDim.x=4, .y=2, .z=4。

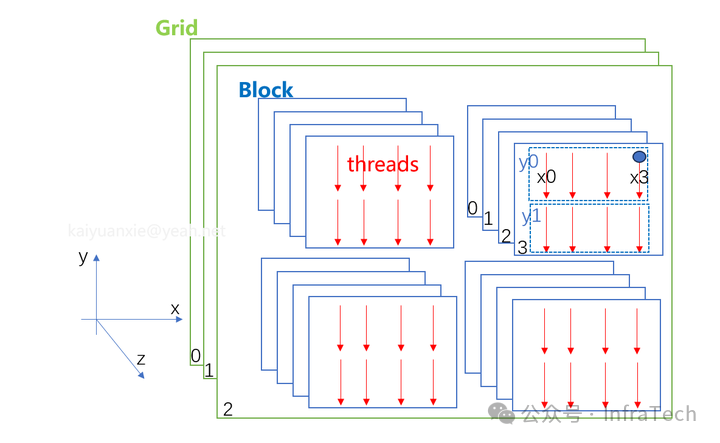
图1：CUDA网格（Grid）与线程块（Block）组织结构示例

这样，整个Grid包含的Block总数为：2*2*3 = 12；每个Block包含的线程总数为：4*2*4 = 32；因此，线程总数为：12 * 32 = 384。

若要唯一标识一个线程，可以通过其所在的Block索引和线程索引来定位。例如，上图中标记为蓝色的线程，其索引表示为：blockIdx.x=1, .y=0, .z=2； threadIdx.x=3, .y=0, .z=3。

而要获得该线程在所有384个线程中的线性位置（即全局索引），则需要通过公式进行计算。

Part 2: 全局索引计算公式推导

我们的目标是让每个线程通过计算得到的全局索引来访问数据（例如一个一维数组）。由于线程组织结构是两层三维的，计算可以拆分为以下几步：

1. 计算线程在其所属Block内的线性位置 (threadInBlock)。
2. 计算该Block在整个Grid中的线性位置 (blockInGrid)。
3. 计算一个Block包含多少线程 (oneBlockSize)。
4. 综合以上信息，求解线程的全局索引 (idx)。

第一步公式：计算线程在Block内的位置

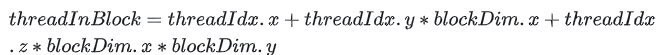
图2：线程在块内的位置计算公式

其中，threadIdx是线程的索引，blockDim是Block的尺寸。以上图为例，单独看一个Block（如下图所示），blockDim.x=4, .y=2, .z=4，threadIdx.x=3, .y=0, .z=3，那么该线程在Block内的位置 threadInBlock 的结果为：

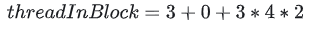
图3：代入具体数值的计算示例

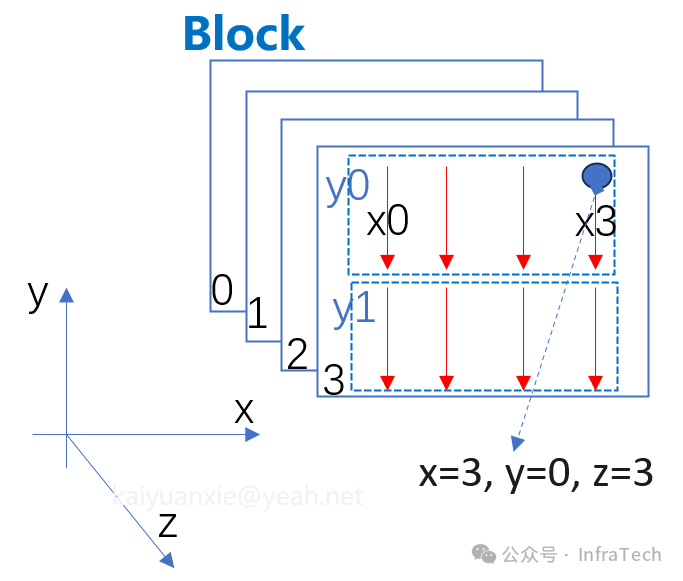
图4：三维线程块（Block）索引示意图

第二步公式：计算Block在Grid中的位置

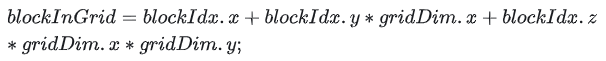
图5：块在网格中的位置计算公式

计算该Block在Grid中的线性位置，需要知道blockIdx和gridDim。继续上面的示例，已知gridDim.x=2, .y=2, .z=3；blockIdx.x=1, .y=0, .z=2；即可得：

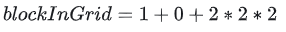
图6：代入具体数值的计算示例

第三步公式：求解全局索引

图7：全局索引计算公式

2.1 全3D结构：3D Grid与3D Block

这是最通用的形式，代码如下：

__global__ void kernel3D3D(float *input, int dataNum)
{
    // 线程在Block中位置计算：
    int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    // Block在整个Grid中的位置计算：
    int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    // 一个Block有多少个线程：
    int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    // 全局位置索引：
    int idx = threadInBlock + oneBlockSize*blockInGrid;
}

基于这个全3D的通用公式，通过将不需要的维度大小设为1，对应的索引设为0，可以推导出所有其他维度的组合公式。简化顺序一般是从Z维度开始，再到Y维度。

2.2 全2D结构：2D Grid与2D Block

令 threadIdx.z = 0; blockIdx.z = 0; blockDim.z = 1; gridDim.z = 1;，代入3D公式简化：

__global__ void kernel2D2D(float *input, int dataNum)
{
    // int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    // int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    // int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    // int idx = threadInBlock + oneBlockSize*blockInGrid;
    // when:
    // threadIdx.z = 0; blockIdx.z = 0;
    // blockDim.z = 1; gridDim.z = 1;
    // then:
    // int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x;
    // int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x;
    // int oneBlockSize = blockDim.x*blockDim.y;
    int idx = threadIdx.x + threadIdx.y*blockDim.x + blockDim.x*blockDim.y*(blockIdx.x + blockIdx.y*gridDim.x);
    // 线程溢出偏移量 = blockDim.x*blockDim.y*gridDim.x*gridDim.y;
}

2.3 全1D结构：1D Grid与1D Block

令 threadIdx.y = 0; threadIdx.z = 0; blockIdx.y= 0; blockIdx.z = 0; blockDim.y = 1; blockDim.z = 1; gridDim.y = 1; gridDim.z = 1;，代入3D公式简化：

__global__ void kernel1D1D(float *input, int dataNum)
{
    // int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    // int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    // int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    // int idx = threadInBlock + oneBlockSize*blockInGrid;
    // when:
    // threadIdx.y = 0; threadIdx.z = 0; blockIdx.y= 0;  blockIdx.z = 0;
    // blockDim.y = 1; blockDim.z = 1; gridDim.y = 1; gridDim.z = 1;
    // then:
    // int threadInBlock = threadIdx.x;
    // int blockInGrid = blockIdx.x;
    // int oneBlockSize = blockDim.x;
    int idx = threadIdx.x + blockIdx.x * blockDim.x;
    // 线程溢出偏移量 = blockDim.x*gridDim.x;
}

2.4 其他混合维度结构

你可以根据数据结构的需求，构建任意维度的线程组织形式。方法依然是：需要的维度保留计算，不需要的维度将其大小设置为1，索引设置为0，然后从通用3D公式推导即可。

例如，2D Grid与3D Block：Grid的Z维度未使用，设置 blockIdx.z=0; gridDim.z=1；

__global__ void kernel2D3D(float *input, int dataNum)
{
    // int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    // int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    // int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    // int idx = threadInBlock + oneBlockSize*blockInGrid;
    // when
    // blockIdx.z = 0;
    // then
    int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x;
    int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    int idx = threadInBlock + oneBlockSize*blockInGrid;
}

再如，3D Grid与2D Block：Block的Z维度未使用，设置 threadIdx.z=0; blockDim.z=1;

__global__ void kernel3D2D(float *input, int dataNum)
{
    // int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x + threadIdx.z*blockDim.x*blockDim.y;
    // int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    // int oneBlockSize = blockDim.x*blockDim.y*blockDim.z;
    // int idx = threadInBlock + oneBlockSize*blockInGrid;
    // when
    // threadIdx.z=0; blockDim.z=1;
    // then
    int threadInBlock = threadIdx.x + threadIdx.y*blockDim.x;
    int blockInGrid = blockIdx.x + blockIdx.y*gridDim.x + blockIdx.z*gridDim.x*gridDim.y;
    int oneBlockSize = blockDim.x*blockDim.y;
    int idx = threadInBlock + oneBlockSize*blockInGrid;
}

类似地，还有1D Grid-2D Blocks（矩阵计算中常用）、1D Grid-3D Blocks等，方法相同，此处不再赘述。

Part 3: 示例代码

3.1 打印线程的全局索引

可以通过打印所有线程的索引来检验计算是否正确，例如打印一个2D Grid与2D Block的线程结构：

__global__ void printIdx2D2D()
{
    int i = threadIdx.x + threadIdx.y*blockDim.x + blockDim.x*blockDim.y*(blockIdx.x + blockIdx.y*gridDim.x);
    printf("Global idx %d, threadIdx.x: %d, threadIdx.y: %d threadIdx.z: %d, blockIdx.x: %d, blockIdx.y: %d,  blockIdx.z: %d \n",\
    i, threadIdx.x, threadIdx.y, threadIdx.z, blockIdx.x, blockIdx.y, blockIdx.z);
}

使用 grid 3 x 3, block 2 x 2，总线程数为36 (3x3x2x2)，调用方式如下：

printIdx2D2D<<<dim3(3, 3), dim3(2,2)>>>();

打印结果如下所示。可以看到Global idx (0~35) 每个线程的全局索引都相互独立，且各不相同：

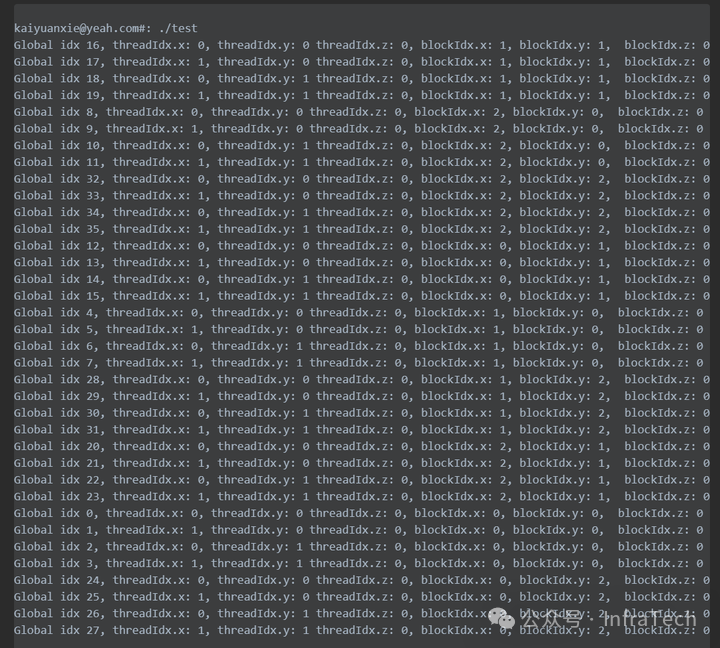
图8：全局索引打印输出示例

3.2 构建功能测试用例

计算目标：用CUDA线程对数组中的每个元素执行加1运算。通过CPU的运算结果来校验CUDA核函数的正确性。
如果全局索引映射关系计算错误，可能导致数据被重复计算或漏算，最终结果错误；如果映射正确，则GPU计算结果应与CPU结果完全一致。测试代码逻辑如下：

#define TOTAL_SIZE 5000
#define N 4
#define M 4
using kernel = void (*)(float *, int);

bool test(kernel func, dim3 BlocksPerGrid, dim3 threadsPerBlock) {
    unsigned int totalSize = TOTAL_SIZE;
    float* hostData = (float*) malloc(sizeof(float) * totalSize); // 主机数据
    float* checkData = (float*) malloc(sizeof(float) * totalSize);  // 校验数据
    float* devicePtr;
    checkCudaErrors(cudaMalloc((void**)&devicePtr, sizeof(float) * totalSize));
    for (int i =0; i < totalSize; ++i) {
        hostData[i] = i;
        checkData[i] = i + 1; // 校验数据增加1
    }
    checkCudaErrors(cudaMemcpy(devicePtr, hostData,  totalSize * sizeof(float), cudaMemcpyHostToDevice));
    func<<<BlocksPerGrid, threadsPerBlock>>>(devicePtr, totalSize); // 通过GPU进行运算
    checkCudaErrors(cudaMemcpy(hostData, devicePtr, totalSize * sizeof(float), cudaMemcpyDeviceToHost));
    // check result: 此处校验结果
    bool rst = true;
    for (int i =0; i < totalSize; ++i) {
        if (!areFloatsEqual(checkData[i], hostData[i])) {
            rst = false;
            printf("The result not equal in data index %d. expect:%f  result:%f\n", i, checkData[i], hostData[i]);
            break;
        }
    }
    checkCudaErrors(cudaFree (devicePtr));
    free(hostData);
    free(checkData);
    return rst;
}

源码位置：threads_hierarchy_calc.cu

编译与运行：

nvcc -lcuda threads_hierarchy_calc.cu -o test && ./test

---

参考文献:

• [1] https://github.com/CalvinXKY/BasicCUDA/blob/master/common_methods/threads_hierarchy_calc.cu
• [2] https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html
• [3] https://www.cnblogs.com/tiandsp/p/9458734.html

希望这篇关于CUDA线程索引计算的详细解析能帮助你更好地理解并行计算机基础中的内存访问模型。如果你对更多C/C++底层优化或高性能计算话题感兴趣，欢迎在云栈社区交流探讨。