找回密码
立即注册
搜索
热搜: Java Python Linux Go
云栈社区»论坛 › 技术文档「 Note & Doc 」 › GPU Merge Path并行归并排序：原理、CUDA实现与性能优化 ...
发回帖 发新帖
云栈大前端

1852

积分

0

好友

240

主题

GPU Merge Path并行归并排序：原理、CUDA实现与性能优化

发表于 15 小时前 | 查看: 2| 回复: 0

本文深入探讨GPU Merge Path算法，这是一种专门为图形处理器设计的并行合并算法。我们从传统归并排序的局限性出发，详细推导了GPU Merge Path的数学模型和算法原理。通过二维网格表示、对角线分割和并行路径查找，该算法实现了高效的负载均衡和内存访问优化。本文包含完整的数学公式推导、Python伪代码实现、CuPy实际代码示例以及性能分析，展示了算法在大规模数据处理中的优势。

1. 传统归并排序的局限性

传统归并排序采用分治策略，其核心是合并两个有序序列的过程。给定两个有序序列：

其中 ，。传统合并算法的伪代码如下：

def merge_serial(A, B):
    m, n = len(A), len(B)
    C = [0] * (m + n)
    i = j = k = 0

    while i < m and j < n:
        if A[i] <= B[j]:
            C[k] = A[i]
            i += 1
        else:
            C[k] = B[j]
            j += 1
        k += 1

    while i < m:
        C[k] = A[i]
        i += 1
        k += 1

    while j < n:
        C[k] = B[j]
        j += 1
        k += 1

    return C

该算法具有固有的串行性，体现在：

  1. 每次比较-复制操作依赖于前一次操作的结果
  2. 循环变量i和j的更新是顺序的
  3. 输出位置k是顺序递增的

时间复杂度为 ，空间复杂度为 。在CPU上，这种串行算法是高效的，但在GPU上，由于拥有数千个计算核心，串行算法无法充分利用硬件资源。

2. GPU Merge Path的数学基础

2.1 二维网格表示法

将合并过程表示为一个 的二维网格。网格中的每个单元格 表示一个状态：

  • ：已从序列 中取出的元素数量
  • ：已从序列 中取出的元素数量

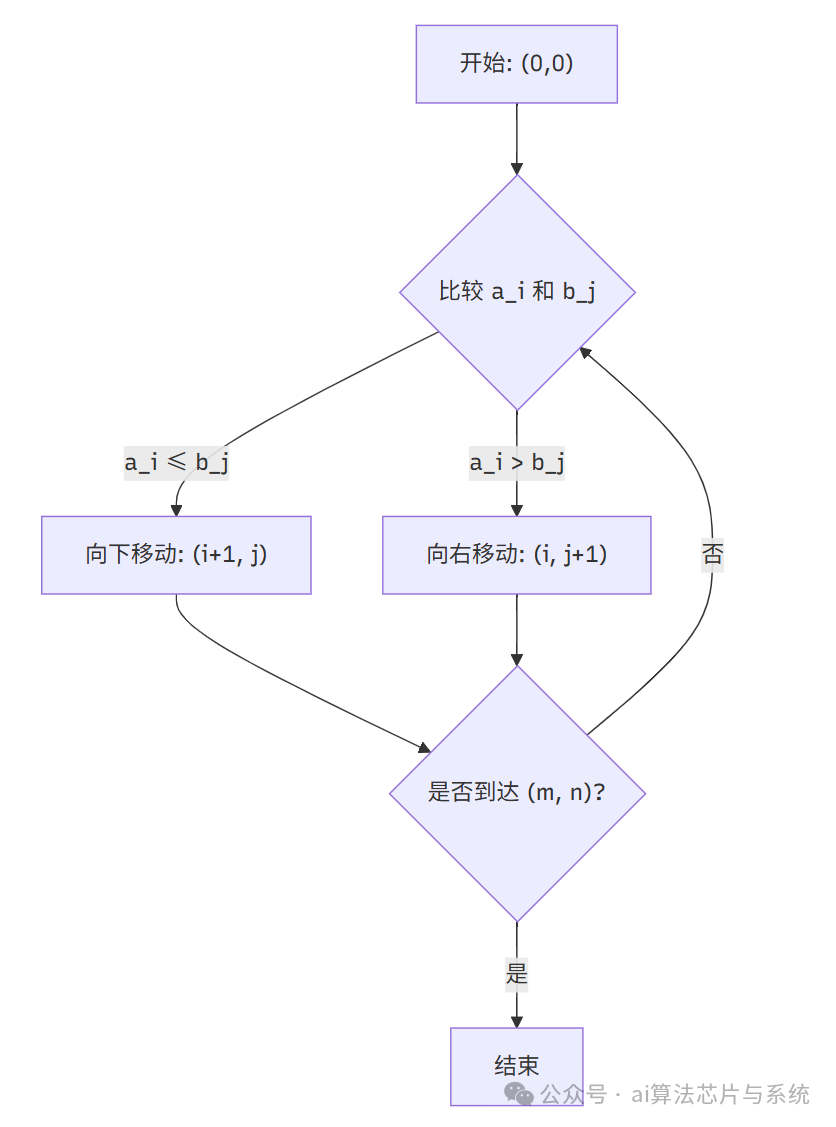
GPU Merge Path算法流程图-路径选择

从起点 到终点 的每一条路径都代表一种可能的合并顺序。

2.2 对角线定义

定义对角线 为满足 的所有点 的集合。对角线 对应合并后的第 个位置。

数学表达式：

对于 ，总共有 条对角线。

2.3 合并路径定义

合并路径 是从 到 的一条特定路径，满足以下条件：

对于路径上的每个点 ，其中 ：

  1. 起始条件：
  2. 终止条件：
  3. 对角线约束：
  4. 路径规则：
    • 如果 ，则 （向下移动）
    • 否则 （向右移动）

2.4 路径点性质

对于对角线 ，合并路径上的点 满足：

其中定义边界条件：

  • 当 时，
  • 当 时，
  • 当 时，
  • 当 时，

这个性质是GPU Merge Path算法的核心，它允许我们并行计算每个对角线的分割点。

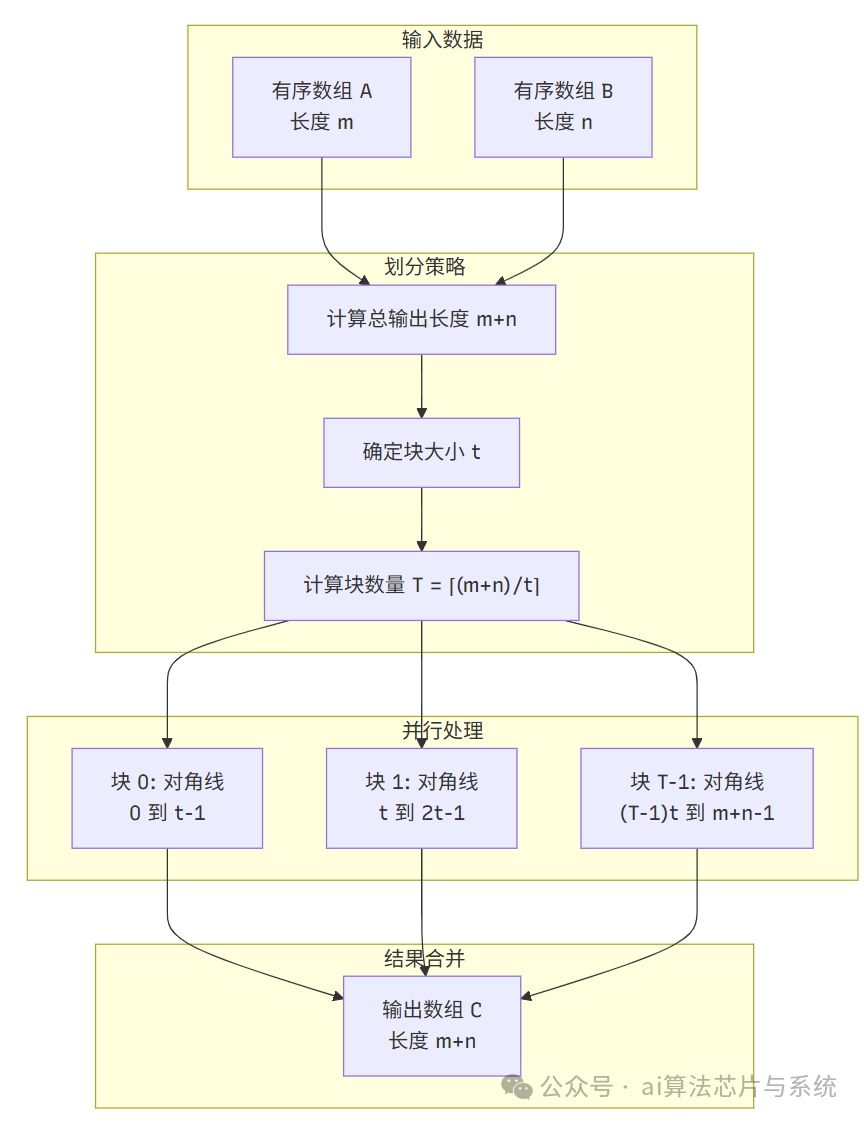
3. 并行化策略与任务分解

3.1 输出数组划分

将输出数组 划分为 个连续的块，每个块大小为 （最后一个块可能较小）。

数学表达式：

第 个块（）包含输出位置：

3.2 块起始点计算

第 个块的起始对角线为：

该块的起始分割点为：

其中 函数使用二分查找算法实现：

def find_split_point(A, B, d):
    m, n = len(A), len(B)
    low = max(0, d - n)
    high = min(d, m)

    while low < high:
        mid = (low + high) // 2

        # 获取a_mid的值，注意边界条件
        a_val = A[mid] if mid < m else float('inf')

        # 获取b_{d-mid-1}的值，注意边界条件
        b_index = d - mid - 1
        b_val = B[b_index] if (0 <= b_index < n) else float('-inf')

        if a_val <= b_val:
            low = mid + 1
        else:
            high = mid

    return low

3.3 负载均衡分析

每个块处理大约 个元素的合并。由于 函数确保每个块的起始点是精确的，因此：

  1. 所有块的处理工作量大致相等
  2. 没有数据依赖关系，可以并行执行

GPU Merge Path并行任务划分示意图

4. 线程块内并行合并算法

4.1 共享内存分配

每个线程块分配共享内存：

  • ：存储 的子数组
  • ：存储 的子数组

实际加载的数据量为：

4.2 数据加载模式

使用跨步模式将数据从全局内存加载到共享内存。对于线程 （），加载：

4.3 并行合并算法

每个线程 负责输出位置 的元素。线程 需要找到在 和 中第 小的元素。

def thread_local_merge(tid, S_A, S_B, tile_size):
    # 在S_A中查找分割点
    low = max(0, tid - tile_size + 1)
    high = min(tid, tile_size - 1)

    while low <= high:
        mid = (low + high) // 2
        a_val = S_A[mid]
        b_idx = tid - mid - 1

        b_val = S_B[b_idx] if b_idx >= 0 else float('-inf')

        if a_val <= b_val:
            low = mid + 1
        else:
            high = mid - 1

    i = low
    j = tid - i

    # 确定最终元素
    a_candidate = S_A[i] if i < tile_size else float('inf')
    b_candidate = S_B[j] if j < tile_size else float('inf')

    return a_candidate if a_candidate <= b_candidate else b_candidate

4.4 算法复杂度分析

每个线程执行：

  1. 一次二分查找：
  2. 两次共享内存访问：
  3. 一次全局内存写入：

总操作次数：

5. 完整算法实现

5.1 CUDA核函数详解

下面我们详细解读GPU Merge Path算法的CUDA核函数实现：

extern "C" __global__
void gpu_merge_path_kernel(
    const float* A,      // 输入数组A
    const float* B,      // 输入数组B
    float* C,           // 输出数组
    int m,              // A的长度
    int n,              // B的长度
    int tile_size       // 每个tile处理的元素数量
){
    // 声明动态共享内存
    extern __shared__ float shared_mem[];
    float* S_A = shared_mem;
    float* S_B = &shared_mem[tile_size];

    int tid = threadIdx.x;      // 线程在线程块内的ID
    int bid = blockIdx.x;       // 线程块ID

    // 1. 计算当前tile的起始对角线
    int d_start = bid * tile_size;

    // 2. 使用二分查找找到分割点
    int low = max(0, d_start - n);
    int high = min(d_start, m);

    while (low < high) {
        int mid = (low + high) / 2;
        float a_val = (mid < m) ? A[mid] : INFINITY;
        int b_index = d_start - mid - 1;
        float b_val = (b_index >= 0 && b_index < n) ? B[b_index] : -INFINITY;

        if (a_val <= b_val) {
            low = mid + 1;
        } else {
            high = mid;
        }
    }

    int i_start = low;
    int j_start = d_start - i_start;

    // 3. 加载数据到共享内存
    int a_idx = i_start + tid;
    int b_idx = j_start + tid;

    if (tid < tile_size) {
        S_A[tid] = (a_idx < m) ? A[a_idx] : INFINITY;
        S_B[tid] = (b_idx < n) ? B[b_idx] : INFINITY;
    }

    __syncthreads();  // 确保所有线程完成数据加载

    // 4. 每个线程处理一个输出位置
    int output_idx = d_start + tid;
    if (output_idx < m + n) {
        // 执行线程局部合并
        int local_low = max(0, tid - tile_size + 1);
        int local_high = min(tid, tile_size - 1);

        while (local_low <= local_high) {
            int mid = (local_low + local_high) / 2;
            float a_val = S_A[mid];
            int b_idx = tid - mid - 1;
            float b_val = (b_idx >= 0) ? S_B[b_idx] : -INFINITY;

            if (a_val <= b_val) {
                local_low = mid + 1;
            } else {
                local_high = mid - 1;
            }
        }

        int i = local_low;
        int j = tid - i;

        float a_candidate = (i < tile_size) ? S_A[i] : INFINITY;
        float b_candidate = (j < tile_size) ? S_B[j] : INFINITY;

        C[output_idx] = (a_candidate <= b_candidate) ? a_candidate : b_candidate;
    }
}

CUDA核函数关键点详解：

  1. 动态共享内存分配
    • 使用extern __shared__声明动态共享内存
    • 前tile_size个元素用于存储A的子数组
    • 后tile_size个元素用于存储B的子数组
  2. 全局分割点查找
    • 每个线程块独立执行二分查找确定起始位置
    • 查找范围：[max(0, d_start - n), min(d_start, m)]
    • 边界条件处理：使用INFINITY和-INFINITY
  3. 数据加载到共享内存
    • 线程使用跨步模式加载数据
    • __syncthreads()确保所有线程完成加载
    • 边界条件：超出数组范围时使用INFINITY
  4. 线程局部合并
    • 每个线程负责计算一个输出元素
    • 在共享内存中进行二分查找
    • 时间复杂度：O(log t)

5.2 CuPy实现与调用

下面是使用CuPy调用CUDA核函数的完整实现：

import cupy as cp
import numpy as np

# 编译CUDA内核
cuda_code = '''
# 上面的CUDA核函数代码
'''

# 编译内核
merge_kernel = cp.RawKernel(cuda_code, 'gpu_merge_path_kernel')

def gpu_merge_path_merge(A, B, tile_size=256):
    """
    使用GPU Merge Path合并两个有序数组

    参数:
        A, B: 两个有序数组 (CuPy数组或可转换为CuPy数组的数据)
        tile_size: 每个tile处理的元素数量

    返回:
        C: 合并后的有序数组
    """
    # 转换为CuPy数组
    if not isinstance(A, cp.ndarray):
        A = cp.array(A, dtype=cp.float32)
    if not isinstance(B, cp.ndarray):
        B = cp.array(B, dtype=cp.float32)

    m, n = len(A), len(B)

    # 分配输出数组
    C = cp.empty(m + n, dtype=cp.float32)

    # 计算tile数量
    num_tiles = (m + n + tile_size - 1) // tile_size

    # 计算共享内存大小（字节）
    shared_mem_size = 2 * tile_size * cp.dtype(cp.float32).itemsize

    # 启动内核
    merge_kernel(
        (num_tiles,),           # 网格大小：tile数量
        (tile_size,),           # 块大小：每个tile一个线程块
        (A, B, C, m, n, tile_size),  # 内核参数
        shared_mem_size         # 共享内存大小
    )

    return C

CuPy实现关键点详解：

  1. 内核编译
    • 使用cp.RawKernel编译CUDA代码
    • 需要指定内核函数名gpu_merge_path_kernel
  2. 参数准备
    • 输入数组转换为cp.float32类型
    • 输出数组预先分配内存
    • 计算所需的tile数量
  3. 内核启动参数
    • 网格大小：(num_tiles,)，每个tile对应一个线程块
    • 块大小：(tile_size,)，每个线程块包含tile_size个线程
    • 共享内存：每个线程块需要2 * tile_size * 4字节
  4. 数据验证
    • 使用cp.asnumpy()转换为NumPy数组验证
    • 可添加断言检查排序正确性

5.3 优化版迭代归并排序

def gpu_merge_sort_optimized(arr, tile_size=256):
    """
    优化版迭代式GPU归并排序，减少内存分配和复制

    参数:
        arr: 输入数组
        tile_size: 每个tile处理的元素数量

    返回:
        排序后的数组
    """
    if not isinstance(arr, cp.ndarray):
        arr = cp.array(arr, dtype=cp.float32)

    n = len(arr)

    if n <= tile_size:
        # 小数组直接使用GPU排序
        return cp.sort(arr)

    # 分配工作数组
    temp = cp.empty_like(arr)
    src = arr
    dst = temp

    width = 1
    while width < n:
        # 计算每轮需要启动的内核数量
        num_merges = (n + (2 * width) - 1) // (2 * width)

        # 为每个合并操作启动一个内核
        for merge_idx in range(num_merges):
            start = merge_idx * 2 * width
            mid = min(start + width, n)
            end = min(start + 2 * width, n)

            if mid >= end:
                # 如果没有第二个子数组，直接复制到目标数组
                if start < n:
                    dst[start:end] = src[start:end]
                continue

            # 使用GPU Merge Path合并子数组
            left_len = mid - start
            right_len = end - mid

            # 计算tile数量
            total_len = left_len + right_len
            num_tiles = (total_len + tile_size - 1) // tile_size

            # 启动合并内核
            if num_tiles > 0:
                # 计算共享内存大小
                shared_mem_size = 2 * tile_size * cp.dtype(cp.float32).itemsize

                # 启动内核（注意：需要修改内核以支持子数组合并）
                merge_kernel(
                    (num_tiles,),
                    (tile_size,),
                    (src[start:mid], src[mid:end], dst[start:end], 
                     left_len, right_len, tile_size),
                    shared_mem_size
                )

        # 交换源和目标数组
        src, dst = dst, src
        width *= 2

    # 如果最终结果在临时数组中，复制回原数组
    if src is not arr:
        arr[:] = src[:]

    return arr

迭代归并排序详解：

  1. 迭代式归并
    • 从宽度1开始，逐步扩大合并区间
    • 每轮合并相邻的有序子数组
    • 时间复杂度：
  2. 内存优化
    • 使用两个数组交替作为源和目标
    • 减少不必要的内存分配和复制
    • 最终结果可能保存在原数组或临时数组
  3. 并行合并
    • 每个合并操作使用GPU Merge Path算法
    • 支持任意大小的子数组合并
    • 充分利用GPU并行性

6. 算法分析

6.1 时间复杂度分析

设GPU有 个处理器核心，每个核心可同时执行一个线程。

理想情况下的并行时间复杂度：

与传统算法对比：
传统合并算法：

加速比：

当 很大时：

6.2 空间复杂度分析

全局内存：

  • 输入：
  • 输出：
    总全局内存使用：

共享内存：
每个线程块：
总共享内存使用： （但不同时使用）

寄存器：
每个线程：常数个寄存器
总寄存器使用：

6.3 内存访问模式分析

全局内存访问：

  1. 加载阶段：合并访问模式
    • 线程 访问
    • 相邻线程访问相邻内存地址
    • 最大化内存带宽利用率
  2. 存储阶段：合并访问模式
    • 线程 写入
    • 相邻线程写入相邻内存地址

共享内存访问：

  1. 加载到共享内存：跨步访问
  2. 从共享内存读取：随机访问（二分查找）
  3. 银行冲突：由于二分查找的随机性，可能产生银行冲突

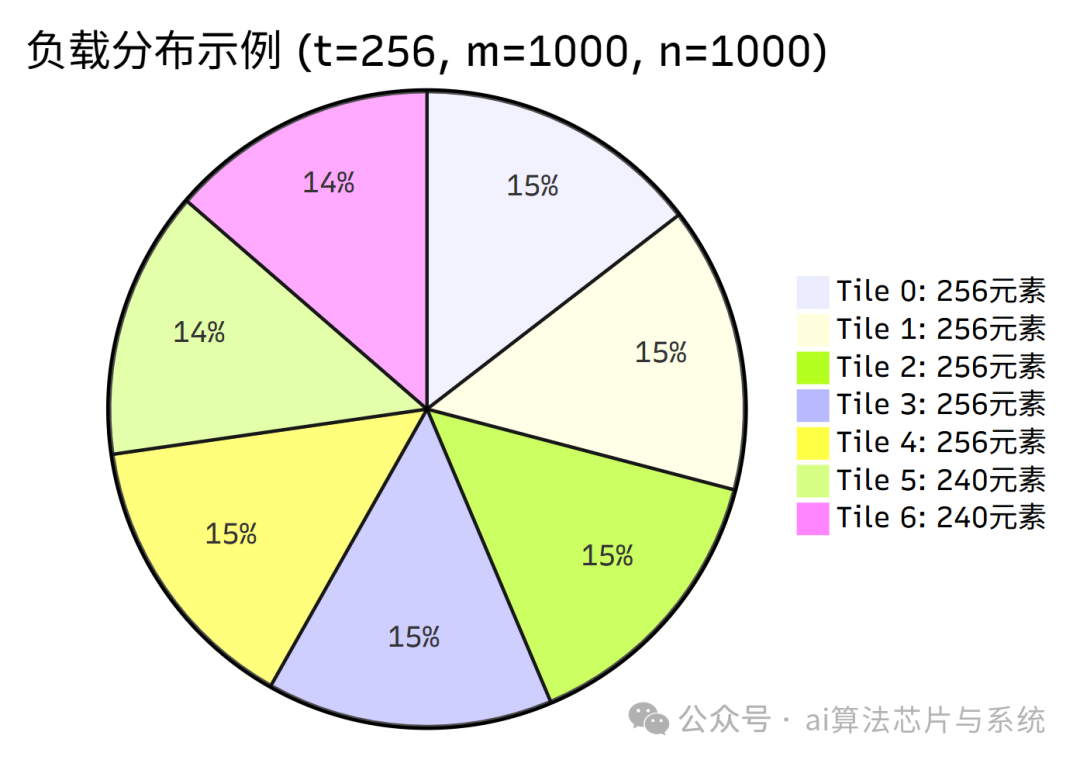
6.4 负载均衡分析

每个tile处理 个输出元素，负载完美均衡。

实际负载由以下因素决定：

其中：

GPU Merge Path负载分布示例图

7. 性能优化策略

7.1 Tile大小选择

Tile大小 的选择需要考虑多个因素：

  1. 共享内存限制： 受限于GPU共享内存大小
  2. 线程块大小： 通常等于线程块大小
  3. 负载均衡：更大的 可能减少tile数量，但增加每个线程的工作量

优化公式：

其中 是共享内存大小， 是元素大小（字节）。

7.2 内存访问优化

7.2.1 合并访问

确保全局内存访问模式满足：

  1. 相邻线程访问相邻内存地址
  2. 内存地址对齐到128字节边界

7.2.2 共享内存布局

使用数组填充避免共享内存银行冲突：

// 优化后的共享内存分配
__shared__ float S_A[256 + 4];  // 填充4个元素
__shared__ float S_B[256 + 4];  // 填充4个元素

7.3 计算优化

7.3.1 循环展开

展开二分查找循环以减少控制流开销：

// 展开的二分查找
int low = max(0, d_start - n);
int high = min(d_start, m);

// 假设最大迭代次数为10（对应最多1024个元素）
#pragma unroll
for (int iter = 0; iter < 10; iter++) {
    if (low >= high) break;
    int mid = (low + high) >> 1;
    float a_val = (mid < m) ? A[mid] : INFINITY;
    int b_index = d_start - mid - 1;
    float b_val = (b_index >= 0 && b_index < n) ? B[b_index] : -INFINITY;

    if (a_val <= b_val) {
        low = mid + 1;
    } else {
        high = mid;
    }
}

7.3.2 指令级并行

利用GPU的SIMD架构：

  1. 使用向量化加载/存储指令
  2. 使用内联函数减少函数调用开销

7.4 自适应算法选择

根据数据特征选择不同算法：

数据特征 推荐算法 原因
小规模数据 (n < 1024) 直接排序 内核启动开销占主导
高度不平衡数据 GPU Merge Path 负载均衡好
数据已基本有序 改进的Merge Path 减少二分查找迭代

8. 结论

GPU Merge Path算法通过将传统串行合并问题转化为并行路径查找问题，实现了高效的GPU并行合并。算法的关键创新包括：

  1. 二维网格模型：使用 的对角线表示合并进度
  2. 分割点定理： 提供了并行计算的基础
  3. 并行查找算法：二分查找确定分割点，时间复杂度
  4. 负载均衡策略：均匀划分输出数组，确保所有处理单元工作量均衡

算法的时间复杂度为 ，相比串行算法的 ，在数据规模较大时能获得接近线性的加速比。

主要优势：

  • 高并行度：充分利用GPU的数千个计算核心
  • 负载均衡：静态任务分配避免线程空闲
  • 内存访问优化：合并访问模式最大化内存带宽利用率
  • 可扩展性：算法性能随数据规模增加而提高

局限性：

  • 需要输入数组已排序
  • 对于小规模数据，内核启动开销可能占主导
  • 共享内存大小限制了单个tile的最大处理能力

GPU Merge Path算法已在实际系统中广泛应用，特别是在需要处理大规模排序和合并操作的高性能计算和数据分析场景中。通过合理的参数调优和内存访问优化，该算法能够充分发挥GPU的并行计算能力，显著提升数据处理效率。

GPU Merge Path算法演进与性能对比图

GPU Merge Path算法代表了并行计算在数据处理领域的重要进展，通过巧妙的算法设计和硬件特性利用，解决了传统串行算法在并行环境下的局限性，为大规模数据的高效处理提供了有力工具。

如果你想与更多开发者交流并行计算与GPU优化相关的技术，欢迎访问云栈社区获取更多资源与讨论。




上一篇：Go内存泄漏问题排查：从生命周期视角理解内存锚点与根治方案
下一篇：IP归属地是如何被查询到的？原理与实现方法解析
GPU, CUDA, 并行计算, 排序算法, 高性能计算

相关帖子
返回列表
高级模式
B Color Quote Code Smilies
您需要登录后才可以回帖 登录 | 立即注册

手机版|小黑屋|网站地图|云栈社区 ( 苏ICP备2022046150号-2 )

GMT+8, 2026-1-16 21:13 , Processed in 0.226777 second(s), 41 queries , Gzip On.

Powered by Discuz! X3.5

© 2025-2026 云栈社区.

快速回复 返回顶部 返回列表