SwiGLU激活函数深度解析：主流LLM为何放弃ReLU转向它

现代大语言模型（LLM）在前馈网络层中普遍采用 SwiGLU 作为激活函数，而逐渐摒弃了传统的 ReLU。本文将深入探讨这一选择背后的技术原理与优势。

神经网络的核心操作是一系列矩阵乘法。如果仅堆叠线性层而不引入激活函数，无论网络深度如何，其表达能力仍局限于线性变换，无法学习复杂的非线性关系。

激活函数的引入带来了非线性，使得神经网络能够逼近复杂的非线性函数，这是深度学习强大表达能力的基础。

ReLU有什么问题？

ReLU 确实在深度学习发展史上具有革命性意义：它结构简单、计算高效，并有效缓解了 sigmoid 或 tanh 等函数带来的梯度消失问题。

尽管常有人列出 ReLU 的潜在缺陷，如神经元死亡等，但这些大多属于理论担忧，在实际应用中可以通过批量归一化、自适应学习率等现代技术有效避免。

在深入探讨 SwiGLU 之前，我们有必要先了解另一个激活函数——Swish，它是 SwiGLU 的关键组成部分。

Swish 是一种“自门控”激活函数：输入 \(x\) 乘以其自身的 sigoid σ(x)，后者充当一个门，控制有多少输入信号能够通过。

观察门的行为：

• 当 \(x\) 为非常大的负值时：σ(x) ≈ 0，此时门关闭（抑制输出）。
• 当 \(x\) 为非常大的正值时：σ(x) ≈ 1，此时门完全打开（输入几乎原样通过）。

尽管公式稍显复杂，Swish 的函数形态与 ReLU 非常相似。

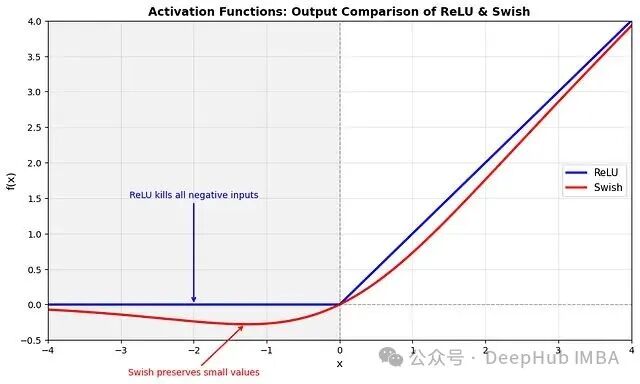
Swish比ReLU更好吗？

实践表明，Swish 的性能通常优于 ReLU。虽然其背后的确切原理如同深度学习的许多现象一样难以完全解释，但我们可以总结出以下关键区别：

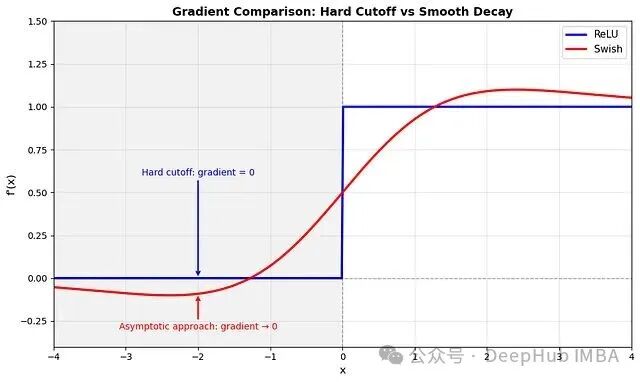
没有硬梯度截断

观察上图，主要区别在于它们如何处理负输入：

• ReLU：在零点进行硬截断。
  当 \(x < 0\) 时：输出 = 0 且梯度 = 0。这就是所谓的“神经元死亡”问题（尽管如前所述，现代技术通常可以缓解）。
• Swish：平滑、渐进地趋近于零。
  对于负的 \(x\)：梯度渐近地趋近于零，但对于有限值永远不会精确等于零。因此理论上神经元始终可以接收到梯度更新（尽管对于极负的输入，更新量可能微乎其微）。

平滑性

ReLU 在 \(x = 0\) 处存在不可导点（导数从0跳变为1）。Swish 在整个定义域内无限可微，这意味着其梯度景观更为平滑。这种平滑性是否直接提升了 Swish 的性能尚无定论，但它很可能对优化过程有所帮助。

什么是门控线性单元（GLU）？

接下来介绍 SwiGLU 的另一个核心组件：GLU（门控线性单元）。其公式为：

\[ \text{GLU}(x) = (xW + b) \odot \sigma(xV + c) \]

其中：

• \(x\) 是输入。
• \(W\) 和 \(V\) 是权重矩阵。
• \(b\) 和 \(c\) 是偏置向量。
• \(\odot\) 表示逐元素乘法。
• \(\sigma\) 是 sigmoid 函数。

GLU 采用了门控机制，在这一点上与 Swish 有相似之处。两者的核心区别在于：GLU 并非对所有特征应用相同的变换（恒等变换）后再用固定函数进行门控，而是使用了两个独立的线性投影：

• \(xW + b\)：对输入进行变换，生成内容路径。
• \(σ(xV + c)\)：决定每个特征应通过多少内容，因此被称为门路径。

因此，GLU 实际上可以看作是 Swish 的一种泛化形式。

逐元素乘法 \(\odot\) 允许门有选择地过滤内容中的各个元素。当 \(σ(xV + c)\) 接近0时，门可以完全抑制某些特征；当它接近1时，则让其他特征完全通过。

门控的具体示例

假设我们有一个4维向量 x = [1.0, -0.5, 2.0, 0.3]。

GLU 对同一输入施加两种变换：

1. 通过内容路径变换内容：xW + b。假设得到 [2.0, -1.5, 3.0, 0.5]。
2. 通过门路径生成门控信号：σ(xV + c)。假设得到 [0.9, 0.1, 0.95, 0.05]。

GLU 的输出是二者的逐元素乘积：
\[ \text{GLU output} = [2.0 × 0.9, -1.5 × 0.1, 3.0 × 0.95, 0.5 × 0.05] = [1.8, -0.15, 2.85, 0.025] \]

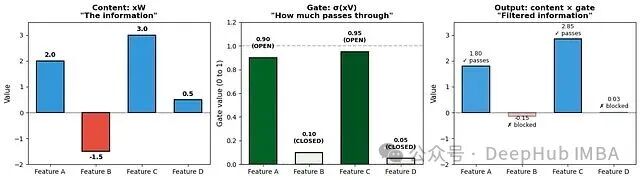
解读结果：

• 特征1：内容为正（2.0），门值高（0.9）→ 强烈通过（1.8）。
• 特征2：内容为负（-1.5），门值低（0.1）→ 被大幅阻挡（-0.15）。
• 特征3：内容为正（3.0），门值极高（0.95）→ 几乎完全通过（2.85）。
• 特征4：内容较小（0.5），门值极低（0.05）→ 被强烈抑制（0.025）。

这样，网络就学会了复杂的决策规则：“对于此类输入，应放大特征1和3，同时抑制特征2和4。”

那么SwiGLU是什么？

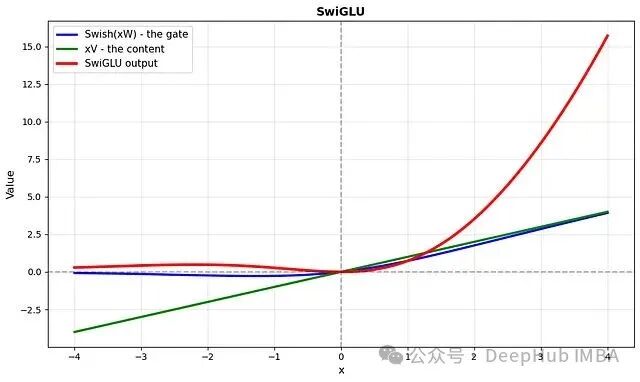
现在，我们将所有组件组合起来。SwiGLU（Swish门控线性单元）简单地融合了 Swish 和 GLU：

\[ \text{SwiGLU}(x) = (xV) \odot \text{Swish}(xW) \]

与 GLU 使用 sigmoid 作为门控函数不同，SwiGLU 使用了 Swish 函数。这正是其名称 Swish + GLU 的由来。

公式中各部分的作用与 GLU 逻辑一致，仅改变了门控函数：

• Swish(xW)：门——决定每个特征有多少信息可以通过。
• xV：内容——需要传输的实际信息。
• \(\odot\)：逐元素乘法——将门控信号应用于内容。

为什么SwiGLU效果这么好？

经验表明，SwiGLU 在 LLM 中的表现优于其他激活函数。其优势根源何在？

乘法交互创建特征组合

比较不同架构的计算过程：

• 标准前馈网络（FFN）（使用ReLU/GELU）：output = activation(xW₁) @ W₂
  每个输出维度是激活后特征的加权和。激活函数是逐元素应用的——特征在激活阶段本身并不相互交互。
• SwiGLU FFN：output = (Swish(xW) ⊙ xV) @ W₂
  逐元素乘法 \(\odot\) 在两条路径之间创造了乘积交互。令 g = Swish(xW)，c = xV，那么在最终投影前，输出维度 \(i\) 是 gᵢ × cᵢ。

这至关重要：gᵢ 和 cᵢ 都是输入特征的线性组合（在 Swish 应用之前）。它们的乘积包含了像 xⱼ × xₖ 这样的交叉项。网络可以通过学习 W 和 V，来放大或抑制特定的输入特征组合。

这与注意力机制强大的原因类似：注意力计算 softmax(QKᵀ)V，其中 QKᵀ 的乘积捕获了查询和键特征之间的交互。SwiGLU 为前馈网络带来了类似的、基于乘法的强大表达能力。

为什么在门中使用Swish而非Sigmoid？

原始 GLU 使用 sigmoid：σ(xW) ⊙ xV。Sigmoid 的问题在于容易饱和。对于绝对值很大的正输入或负输入，σ(x) ≈ 1 或 σ(x) ≈ 0，且梯度 ∂σ/∂x ≈ 0，导致门控信号“冻结”。

Swish 对于正输入不会饱和，其增长近似线性（类似于 ReLU）。这意味着：

• 梯度可以更好地通过门路径反向传播。
• 门可以执行精细的调节，而不仅仅是简单的“开/关”切换。

平滑性

此外，SwiGLU 是无限可微的。这种整体的平滑性可能有助于提升优化的稳定性。

总结

SwiGLU 的强大性能源于其门控机制与乘法交互。通过将输入拆分至两条路径并进行相乘，网络能够学习哪些特征组合是重要的——这与注意力机制通过 QKᵀ 捕获交互的思路异曲同工。

结合 Swish 函数非饱和的梯度特性，使得 SwiGLU 特别适用于大型语言模型。想了解更多关于人工智能和神经网络技术的深入讨论？欢迎在云栈社区与广大开发者交流探讨。