Python实战指南：智能匹配行业与概念ETF的三种算法方法对比

技术背景

许多有经验的交易员会发现，当你对某个行业、概念或板块长期看好，但又面临成分股数量多、选股难度高的问题时，操作起来并不轻松。另一个常见的现象是，在牛市中，指数的整体涨幅常常超过个人精选的股票组合。因此，如果你的目标仅仅是获取该板块的平均收益，即行业的贝塔（Beta）收益，那么思路就需要调整。

此时通常有两个选择：

• 资金雄厚、能力突出者：可以构建整个行业的指数增强组合，通过调整成分股权重，在获取板块贝塔收益的同时，力争捕捉个股的阿尔法（Alpha）收益。这类板块指数增强算法，也是我们深入探讨的重要内容。
• 普通投资者：由于资金可能无法覆盖所有成分股，理性的选择是聚焦于获取板块的整体贝塔收益。这时，投资对应的板块ETF就成了理想选择。正如巴菲特多次建议的，对于大多数普通投资者而言，长期持有指数基金往往是更优的策略。

如果你认同上述观点，那么本文将为你提供一个有力的工具。在实际投资中，你会发现市场上的ETF数量有限，某些特定板块甚至没有直接对应的ETF产品。如何高效地为特定的行业、板块或概念找到匹配度最高的ETF，便成了一个关键问题。本文将系统性地探讨并解决这个问题。

整个分析流程的主要思路，可以参考下图所示，具体含义将在后文详细解读。

使用场景

• 场景1：看好特定行业但选股困难。当你对某个行业（如申万二级行业中的“航天装备”）前景乐观，却又缺乏行业内精选个股的能力或强逻辑时，往往会发现自己选的个股跑不赢行业指数。此时，买入行业ETF是更佳选择。但问题在于，目标行业可能没有直接对应的ETF，却存在许多相关ETF（如卫星ETF、军工ETF、航天ETF）。如何从中选出与目标行业走势最吻合、最“合理”的那个，就需要科学的匹配方法。
• 场景2：看好特定概念或板块指数。你对同花顺、通达信、东方财富等平台的某个概念或板块指数比较看好，同样希望只获取其整体贝塔收益。对于大多数概念板块而言，并没有现成的ETF，这就需要从全市场所有ETF中筛选出走势相关性最高的品种。
• 场景3：匹配自建股票组合。如果你自己构建了一个股票组合，它不与任何现有指数成分股相同，而你只想获取这个组合整体的贝塔收益。同样由于资金问题难以全部买入，你就需要找到一个在收益和风险特征上都与自建组合相似的ETF。本文介绍的算法同样适用于此场景。

实现算法

首先，第一步永远是基础筛选：剔除那些成交量极小、交易不活跃的ETF，确保标的的流动性。

1. 名称匹配法（效果一般）

这显然是一种高效直接的方法，通过Python程序扫描全市场ETF名称，寻找与目标指数名称相似或包含相同关键词的标的。

步骤：

1. 确定目标指数，获取其精确名称。
2. 获取全市场所有ETF的基本信息列表。
3. 调用Python程序进行关键词模糊匹配，并输出结果。

注意：名称匹配法能快速解决很多一级行业或宽基指数的ETF匹配问题。但对于二级行业、细分概念板块等没有直接跟踪ETF的指数，该方法效果有限。

2. 相似度匹配法

我们寻找ETF的根本目的，是找到在收益、回撤、走势形态上与目标指数最相近的那个。这引出了从数据相似性角度出发的数学方法。

第一种：相关性角度

数学上衡量两个序列是否“相似”，最直接的指标就是计算它们在过去一段时间内的相关系数。

那么问题来了，应该选用哪个指标序列来计算相关系数呢？你可以尝试以下两种：

• 收盘价（净值）序列：以起始日期的收盘价为基准（例如设为1），后续计算每日净值（收盘价/起始日收盘价），得到两条净值曲线。然后计算这两条净值时间序列的相关系数，并按相关性大小排序，选择最高的ETF。
• 收益率序列：计算每日的收益率序列。这相当于对净值序列进行了一阶差分，更能反映日度变化的同步性。基于收益率计算的相关性排序，通常准确度更高。

实际应用：以上两种方法从不同角度给出了相关性计算方式。为了提升准确性，我们可以采用多因子思路：取两种方法计算出的相关系数的平均值，作为最终的相似度得分，并选取得分最高的标的。

注意：当最终相关系数低于90%时，我们需要额外考虑其他风险收益指标，如波动率（标准差）、相对收益的最大回撤等，进行综合判断。

第二种：回归分析角度

这种方法旨在考察两条净值曲线是否满足严格的线性关系，相当于在相关系数的基础上，进一步纳入了两者波动幅度的比较。

具体步骤：

1. 以目标指数收益率为因变量（Y），待测ETF收益率为自变量（X），进行OLS线性回归。
2. 分析回归系数（斜率）、截距及残差。
3. 对残差进行统计检验（如t检验），考察其是否显著不为零。
4. 为了检验关系的稳定性，可以采用滚动窗口的方式进行上述计算。

具体代码见后文。

3. 成分股匹配法

以上都是纯数学方法。实际上，ETF与指数联动好坏，根本上取决于其成分股的相似度。这为我们提供了第三种思路：直接进行成分股匹配。

步骤：

1. 分别获取目标指数和待选ETF的最新成分股数据。
2. 计算两者成分股的交集比例（如Jaccard相似系数）。如果超过80%的股票重合，通常可以认为高度相似。

注意：由于篇幅和时间所限，成分股匹配的完整代码未在本文呈现，其实现依赖于稳定的成分股数据源。

综合应用策略

通过上面的介绍，你已经了解了多种ETF匹配方法，它们各有优劣。那么，在实际应用中能否将它们结合起来呢？

答案是肯定的。一个稳健的综合策略如下：

1. 名称匹配法做初筛：快速筛选出名称直接高度相关（相似度>80%）的ETF，这部分标的优先考虑。剩余ETF进入下一轮。
2. 相似度匹配法做检验与二轮筛选：此法有两个作用：其一，对第一步找到的ETF进行定量检验，增加判断的可靠性；其二，对第一步未匹配到的ETF进行相似度计算和排序。即使降低相关系数阈值，也能起到“兜底”搜索的作用。
3. 成分股匹配法最终兜底：对于通过前两步仍未找到理想匹配，或需要极高置信度的情况，可采用成分股匹配法。设定成分股重合比例阈值，基本上能找到匹配的ETF。但建议完成匹配后，仍用相似度匹配法（回归或相关性检验）进行验证，以增加模型的稳定性。

注意：对于一些新上市的ETF，由于历史数据过短，不适合使用相似度匹配法，此时应依赖名称匹配和成分股匹配法。

具体Python代码实现

由于篇幅所限，此处仅展示核心的检验模块（相似度匹配法）的Python代码。部分代码由AI生成，并经笔者调试，确认正确有效。完整的自动化匹配流程代码更为复杂。

import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 方法1：配对样本t检验（检验收益率差值是否显著不为0）
def paired_t_test(ret1, ret2):
    """配对样本t检验"""
    diff = ret1 - ret2
    t_stat, p_value = stats.ttest_1samp(diff, 0)

    print("=== 配对样本t检验结果 ===")
    print(f"收益率差值均值: {diff.mean():.6f}")
    print(f"收益率差值标准差: {diff.std():.6f}")
    print(f"t统计量: {t_stat:.4f}")
    print(f"p值: {p_value:.4f}")

    if p_value < 0.05:
        print("结论: 在5%显著性水平下，拒绝原假设，两个标的收益率不一致")
    else:
        print("结论: 在5%显著性水平下，无法拒绝原假设，两个标的收益率一致")

    return t_stat, p_value

# 方法2：线性回归方法
def regression_approach(ret1, ret2):
    """回归方法检验收益率一致性"""
    # 添加常数项
    X = sm.add_constant(ret2)
    y = ret1

    # 拟合回归模型
    model = sm.OLS(y, X).fit()

    print("\n=== 线性回归分析结果 ===")
    print(model.summary())

    # 检验假设 H0: 截距=0 且 斜率=1 (完全一致)
    hypothesis = 'const = 0, x1 = 1'
    f_test = model.f_test(hypothesis)

    print(f"\n=== 一致性检验（原假设：截距=0且斜率=1）===")

    # 修复这里：直接使用 fvalue 属性，它可能是标量或数组
    try:
        # 尝试作为标量处理
        f_stat = float(f_test.fvalue)
    except:
        # 如果是数组，取第一个元素
        f_stat = f_test.fvalue[0][0] if hasattr(f_test.fvalue, '__getitem__') else f_test.fvalue

    print(f"F统计量: {f_stat:.4f}")
    print(f"p值: {f_test.pvalue:.4f}")

    if f_test.pvalue < 0.05:
        print("结论: 拒绝原假设，两个标的收益率不一致")
    else:
        print("结论: 无法拒绝原假设，两个标的收益率一致")

    return model, f_test

# 方法3：相关性检验
def correlation_test(ret1, ret2):
    """相关性分析"""
    corr, p_value = stats.pearsonr(ret1, ret2)

    print("\n=== 相关性分析 ===")
    print(f"相关系数: {corr:.4f}")
    print(f"相关系数p值: {p_value:.4f}")

    # 检验相关系数是否接近1
    if corr < 0.95:  # 通常认为高相关性表示一致性
        print("提示: 相关系数较低，可能不一致")
    else:
        print("提示: 相关系数较高，可能一致")

    return corr, p_value

# 可视化分析
def visualize_returns(ret1, ret2, label1="标的A", label2="标的B"):
    """可视化收益率对比"""
    fig, axes = plt.subplots(2, 2, figsize=(12, 10))

    # 1. 收益率时间序列
    axes[0, 0].plot(ret1, label=label1, alpha=0.7)
    axes[0, 0].plot(ret2, label=label2, alpha=0.7)
    axes[0, 0].set_title("收益率时间序列对比")
    axes[0, 0].set_ylabel("收益率")
    axes[0, 0].legend()
    axes[0, 0].grid(True, alpha=0.3)

    # 2. 散点图与45度线
    axes[0, 1].scatter(ret2, ret1, alpha=0.5, s=10)
    # 添加45度线（如果一致，点应该在这条线上）
    min_val = min(ret1.min(), ret2.min())
    max_val = max(ret1.max(), ret2.max())
    axes[0, 1].plot([min_val, max_val], [min_val, max_val],
                    'r--', label='完全一致线')
    axes[0, 1].set_xlabel(f"{label2}收益率")
    axes[0, 1].set_ylabel(f"{label1}收益率")
    axes[0, 1].set_title("收益率散点图")
    axes[0, 1].legend()
    axes[0, 1].grid(True, alpha=0.3)

    # 3. 收益率差值分布
    diff = ret1 - ret2
    axes[1, 0].hist(diff, bins=30, edgecolor='black', alpha=0.7)
    axes[1, 0].axvline(x=0, color='r', linestyle='--', label='零差值')
    axes[1, 0].axvline(x=diff.mean(), color='g', linestyle='-',
                       label=f'均值: {diff.mean():.6f}')
    axes[1, 0].set_xlabel("收益率差值")
    axes[1, 0].set_ylabel("频数")
    axes[1, 0].set_title("收益率差值分布")
    axes[1, 0].legend()
    axes[1, 0].grid(True, alpha=0.3)

    # 4. 累积收益率对比
    cum_ret1 = np.cumprod(1 + ret1) - 1
    cum_ret2 = np.cumprod(1 + ret2) - 1
    axes[1, 1].plot(cum_ret1, label=label1)
    axes[1, 1].plot(cum_ret2, label=label2)
    axes[1, 1].set_title("累积收益率对比")
    axes[1, 1].set_xlabel("时间")
    axes[1, 1].set_ylabel("累积收益率")
    axes[1, 1].legend()
    axes[1, 1].grid(True, alpha=0.3)

    plt.tight_layout()
    plt.show()

    # 计算跟踪误差
    tracking_error = diff.std() * np.sqrt(252)  # 年化跟踪误差
    print(f"\n年化跟踪误差: {tracking_error:.4f}")

# 执行所有检验
def comprehensive_analysis(ret1, ret2, label1="标的A", label2="标的B"):
    """综合分析方法"""
    print("="*60)
    print(f"分析 {label1} 与 {label2} 收益率一致性")
    print("="*60)

    # 基本统计量
    print("\n=== 基本统计量 ===")
    print(f"{label1}: 均值={ret1.mean():.6f}, 标准差={ret1.std():.6f}")
    print(f"{label2}: 均值={ret2.mean():.6f}, 标准差={ret2.std():.6f}")

    # 执行各种检验
    paired_t_test(ret1, ret2)
    regression_approach(ret1, ret2)
    correlation_test(ret1, ret2)

    # 可视化
    visualize_returns(ret1, ret2, label1, label2)

if __name__ == "__main__":
    # 生成示例数据（实际使用时替换为你的数据）
    # np.random.seed(42)
    # n = 250  # 假设250个交易日
    # ret_A = np.random.normal(0.0005, 0.02, n)  # 标的A日收益率
    # ret_B = np.random.normal(0.0005, 0.02, n)  # 标的B日收益率

    # 示例：读取沪深300指数(000300.SH)与其ETF(510300.SH)的历史数据
    df_a = pd.read_csv('000300.SH.csv')
    df_a = df_a[['date', 'close']].copy()
    df_a['date'] = pd.to_datetime(df_a['date']).dt.date
    df_a.set_index('date', inplace=True)
    df_a.rename(columns={"close": '000300.SH'}, inplace=True)

    df_b = pd.read_csv('510300.SH.csv')
    df_b = df_b[['date', 'close']].copy()
    df_b['date'] = pd.to_datetime(df_b['date']).dt.date
    df_b.set_index('date', inplace=True)
    df_b.rename(columns={"close": '510300.SH'}, inplace=True)

    # 合并数据，对齐时间索引
    df = pd.merge(df_a, df_b, right_index=True, left_index=True, how='inner')
    df.sort_index(inplace=True, ascending=True)

    # 计算日收益率
    df = df.pct_change()
    df.dropna(inplace=True)

    # 提取收益率序列
    ret_A = np.array(df['000300.SH'])
    ret_B = np.array(df['510300.SH'])

    n = len(df.index)

    # 运行综合分析
    comprehensive_analysis(ret_A, ret_B, "000300.SH", "510300.SH")

    # 示例：检验两个高度相关的标的（模拟一个几乎完全跟踪的ETF）
    print("\n" + "=" * 60)
    print("示例：检验两个高度相关的标的")
    print("=" * 60)

    # 创建高度相关的两个标的
    ret_C = ret_A + np.random.normal(0, 0.001, n)  # 在原始收益率上添加微小噪声
    comprehensive_analysis(ret_A, ret_C, "000300.SH", "模拟高度相关ETF")

这段代码综合运用了 Pandas、NumPy、Statsmodels 等强大的 Python 数据分析库，是进行智能化金融数据分析的典型案例。

结果验证与分析

我们以沪深300指数（000300.SH）与其主要的场内ETF（510300.SH）为例进行验证。

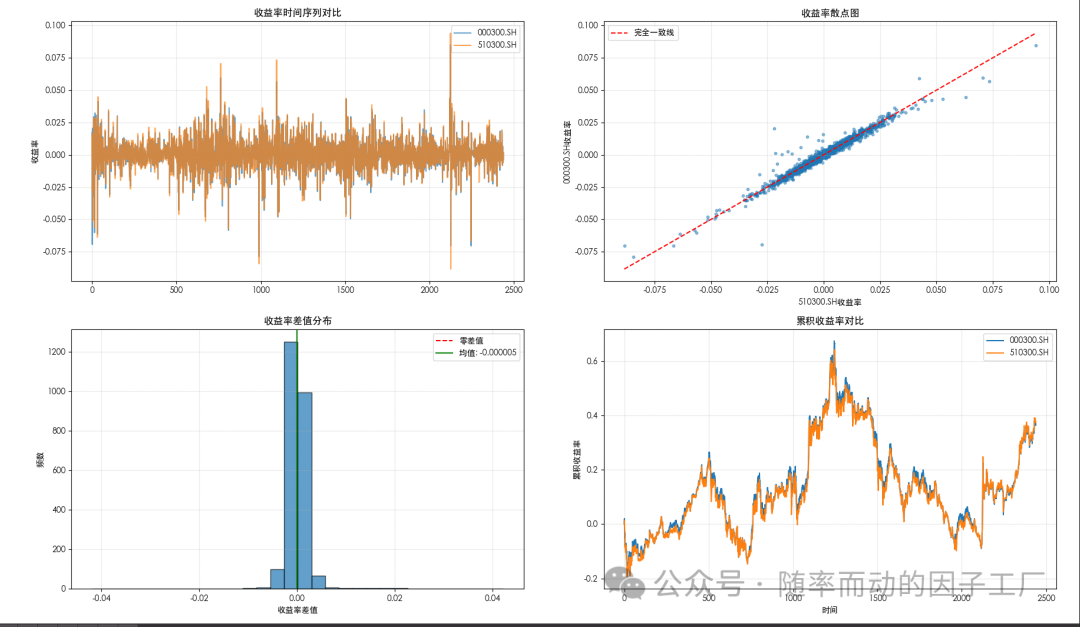
1. 可视化直观对比：下图从四个维度展示了分析结果。左上为日收益率序列对比，右上为收益率散点图及“完全一致”参考线，左下为收益率差值的分布，右下为累积收益率走势对比。从图形上可以直观判断两者匹配度极高。

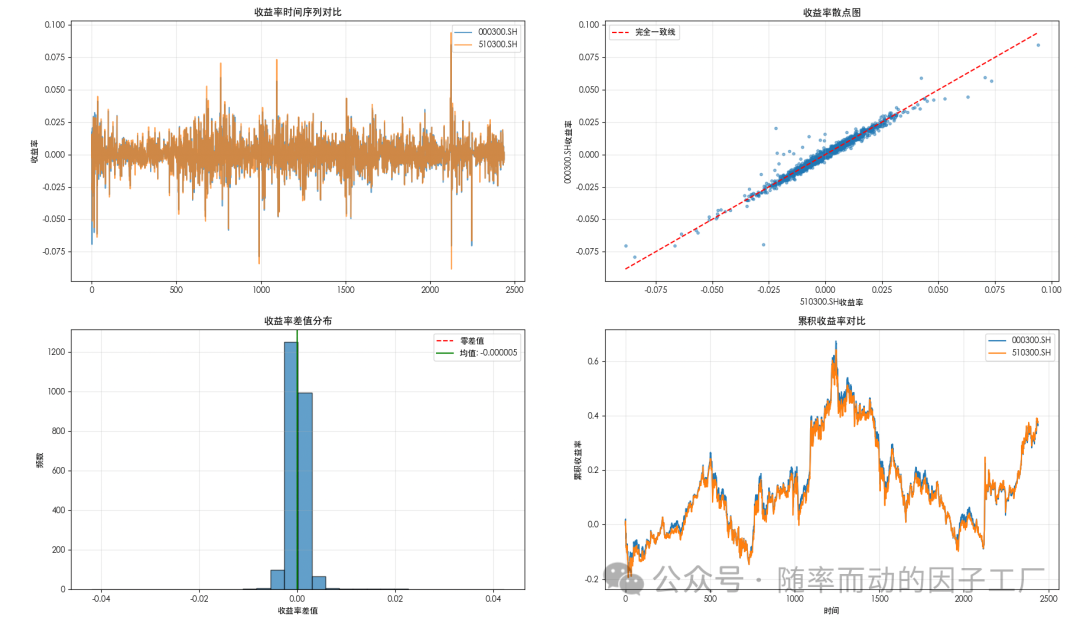
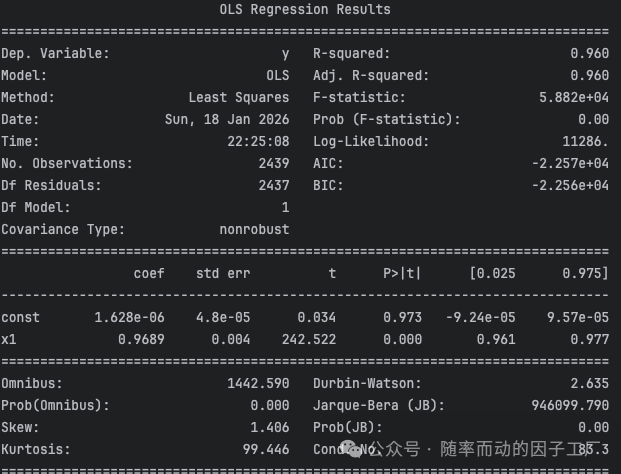
2. 统计与回归检验结果：以下两张图展示了详细的定量分析结果。第一张是基本统计量与配对样本t检验结果，第二张是OLS线性回归的详细摘要。数据显示，两者收益率差值均值接近于0，t检验p值远大于0.05，无法拒绝“收益率一致”的原假设；回归模型的斜率接近1，截距接近0，F检验也支持两者一致的结论。

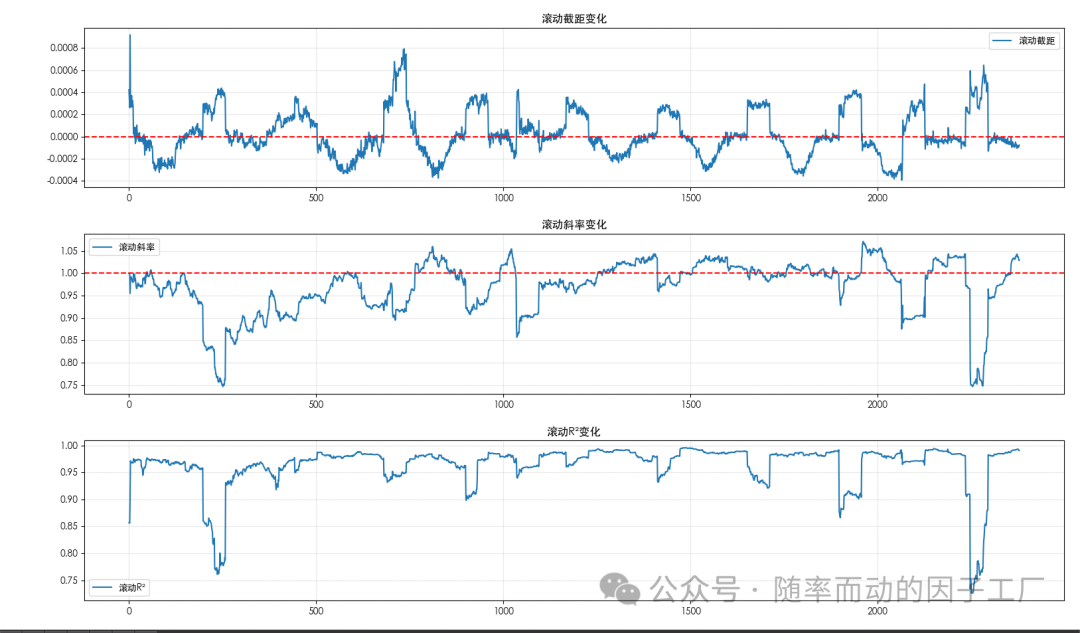
3. 滚动回归稳定性检验：为了考察两者关系是否随时间稳定，我们进行滚动回归。下图展示了滚动窗口下的截距、斜率和R²的变化情况。可以看到，滚动截距在零附近窄幅波动，滚动斜率稳定在1附近，滚动R²始终保持在高位，这证明两者的跟踪关系非常稳定，相对收益序列是平稳的。

定期维护更新频率

由于市场上有新的ETF成立，或现有ETF的成分股会定期调整，我们建立的匹配数据库需要定期维护更新，并重新运行匹配程序。这对于构建行业轮动或主题投资组合尤为重要。通常来说，月度更新一次即可满足大多数策略的需求。

总结

通过本文的阐述，你应该已经清晰地掌握了为特定投资标的寻找匹配ETF的系统性方法。我们涵盖了大部分常见场景的解决方案，并提供了从算法原理、Python代码实现到结果检验的完整流程。将名称匹配、收益相似度匹配和成分股匹配这三种方法结合使用，能够显著提升匹配的准确性和可靠性。

当然，方法不止于此。量化投资领域广阔，如果你有更好的思路或更巧妙的解决方案，欢迎在技术社区进行分享与探讨，例如在 云栈社区 这样的平台与更多同行交流，共同进步。感谢你的阅读。