t-SNE降维技术详解：原理、Python实现与高维数据可视化应用

t-SNE（t-distributed Stochastic Neighbor Embedding）是一种强大的非线性降维方法。它的核心思想是在两个不同的概率空间中匹配数据点之间的相似性关系，从而在低维空间（通常是2D或3D）中保留高维数据的局部结构，形成清晰的簇，特别适用于高维数据的可视化分析，如图像特征、文本嵌入等场景。

核心原理

给定高维样本集 {x_i}，目标是找到对应的低维嵌入表示 {y_i}。

高维相似度（条件概率与对称化）

首先，t-SNE 在高维空间中用高斯分布来衡量样本间的邻近关系。

• 对每个样本 x_i，以自适应带宽 σ_i 的高斯核定义它选择 x_j 作为邻居的条件概率：

  p_{j|i} = \frac{\exp(-||x_i - x_j||^2 / 2σ_i^2)}{\sum_{k \neq i} \exp(-||x_i - x_k||^2 / 2σ_i^2)}

• 为使相似度度量对称，定义联合概率 P：

  p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}

• 每个点的高斯核带宽 σ_i 由困惑度（perplexity）控制。困惑度可以理解为对每个点有效邻居数量的平滑度量，通常设置在5到50之间。算法通过二分搜索为每个 x_i 寻找合适的 σ_i，使得其条件概率分布的困惑度等于用户设定的目标值。

低维相似度（t分布）

在低维嵌入空间中，t-SNE 使用自由度为1的学生t分布（即柯西分布）来定义点 y_i 和 y_j 之间的相似度 q_{ij}：

q_{ij} = \frac{(1 + ||y_i - y_j||^2)^{-1}}{\sum_{k \neq l} (1 + ||y_k - y_l||^2)^{-1}}

选用重尾的 t 分布是为了缓解“拥挤问题”（crowding problem）——即高维空间中许多相距中等距离的点，映射到低维空间时可能会被挤在一起。t 分布允许较远的点保持一定的相似度，从而在低维空间中为不同簇腾出空间。

目标函数（KL散度）

t-SNE 的目标是让低维空间中的相似度分布 Q 尽可能地匹配高维空间的相似度分布 P。衡量两个分布差异的指标是 Kullback-Leibler 散度（KL散度）：

C = KL(P || Q) = \sum_{i} \sum_{j \neq i} p_{ij} \log \frac{p_{ij}}{q_{ij}}

通过最小化这个代价函数 C，优化低维嵌入 {y_i}。

梯度与优化

t-SNE 使用梯度下降法来最小化 KL 散度。代价函数 C 对低维坐标 y_i 的梯度为：

\frac{\delta C}{\delta y_i} = 4 \sum_{j \neq i} (p_{ij} - q_{ij})(y_i - y_j)(1 + ||y_i - y_j||^2)^{-1}

优化过程中通常会结合动量项和早期夸张（early exaggeration）技巧。在早期迭代阶段，将所有 p_{ij} 乘以一个较大的因子（如4），放大数据点之间的吸引力，有助于形成更清晰的全局结构，之后恢复正常值进行精细调整。

直观理解：优化过程就像在低维空间中进行一场“拔河比赛”。

• 在高维空间中相近的点（p_{ij} 大），会受到强大的吸引力，使它们在低维中也靠近。
• 在高维中不相似的点（p_{ij} 很小），其相互作用几乎为零。
• 重尾的 t 分布作为低维相似度模型，天然地对中长距离的点产生排斥力，防止所有点塌缩到同一个点，从而促成清晰簇的形成。

Python 实现与可视化对比

为了直观展示 t-SNE 的效果，我们使用经典的“瑞士卷”数据集进行演示。瑞士卷是一个三维空间中的非线性流形（像一个卷起来的薄片），线性降维方法（如 PCA）很难将其展开，而 t-SNE 这类非线性方法则能较好地保留其局部邻域结构。

以下是完整的 Python 实现代码，我们将生成瑞士卷数据，并对比 PCA（线性）和 t-SNE（非线性）的降维可视化结果。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# 1) 生成瑞士卷数据
n_samples = 5500
X, t = make_swiss_roll(n_samples=n_samples, noise=1.0, random_state=42)
colors = t

# 2) PCA二维投影（线性降维，对比用）
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X)

# 3) t-SNE二维嵌入（非线性降维）
tsne = TSNE(
    n_components=2,
    perplexity=30,
    learning_rate=200,
    n_iter=1000,
    init='pca',           # 常用初始化
    random_state=42,
    verbose=1,
)
X_tsne = tsne.fit_transform(X)

# 4) 可视化分析
fig, axes = plt.subplots(1, 2, figsize=(12, 5), dpi=140, facecolor='white')

# 左：PCA
sc1 = axes[0].scatter(X_pca[:, 0], X_pca[:, 1], c=colors, cmap='rainbow', s=8, edgecolors='none')
axes[0].set_title('PCA 2D Projection (Linear)', fontsize=12)
axes[0].set_xlabel('PC1')
axes[0].set_ylabel('PC2')

# 右：t-SNE
sc2 = axes[1].scatter(X_tsne[:, 0], X_tsne[:, 1], c=colors, cmap='rainbow', s=8, edgecolors='none')
axes[1].set_title('t-SNE 2D Embedding (Nonlinear)', fontsize=12)
axes[1].set_xlabel('Dim 1')
axes[1].set_ylabel('Dim 2')

cbar = fig.colorbar(sc2, ax=axes.ravel().tolist(), shrink=0.9)
cbar.set_label('Manifold Position (t)', rotation=270, labelpad=12)

plt.tight_layout()
plt.show()

运行上述代码后，我们将得到PCA与t-SNE的降维效果对比图。

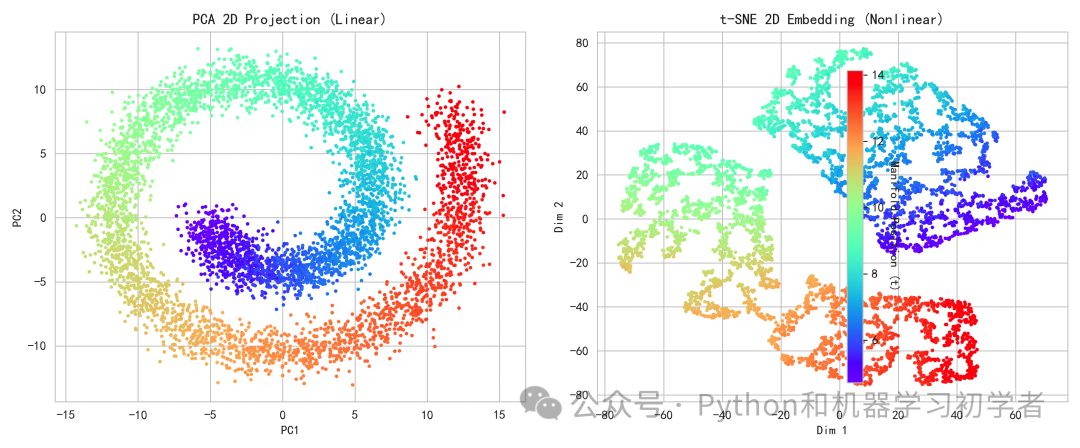
• 左图（PCA）：由于PCA是一种线性投影方法，它试图在全局方差最大的方向上投影数据。对于瑞士卷这种非线性流形，PCA无法“展开”其结构，导致不同部分的点在二维平面上混杂在一起，颜色（对应原始流形上的位置）分布混乱。
• 右图（t-SNE）：t-SNE通过匹配高维空间的局部邻域概率分布，成功地在二维平面上将瑞士卷“展开”。可以看到，颜色呈现出从一端到另一端的连续、平滑过渡，原始流形上的局部邻域关系得到了很好的保持，形成了一个清晰的带状结构。这完美地展示了t-SNE在捕捉非线性结构和进行高维数据可视化方面的强大能力。

总结

t-SNE 以其卓越的局部结构保持能力，已成为高维数据可视化领域的标杆算法之一。理解其背后基于概率分布匹配和梯度下降优化的原理，有助于我们更好地应用和调参。在实践中，需要注意 t-SNE 的计算复杂度较高，且结果受困惑度等参数影响较大，通常需要多次尝试以获得最佳可视化效果。它更多是探索数据的工具，而非特征提取的前置步骤。对于想深入探索更多机器学习算法实践的朋友，可以关注云栈社区上的相关技术讨论与分享。