感知器模型原理解析与实战：人工神经网络的鼻祖

在人工智能浪潮席卷全球的今天，ChatGPT 等大模型（LLM）展现出的强大能力令人惊叹。然而，驱动这些庞然大物的核心引擎——人工神经网络，其最初的形态可以追溯到 60 多年前一个极其简单的数学模型。

今天，我们将深入探讨这位神经网络的鼻祖：感知器（Perceptron）。

01 1957 年的“梦幻起点”

1957 年，康奈尔大学的心理学家弗兰克·罗森布拉特（Frank Rosenblatt）受人类大脑神经元的启发，提出了 “感知器（perceptron）” 模型。

感知器是人类历史上第一个用算法精确定义的神经网络。

从结构上看，感知器由输入层和输出层组成。输入层负责接收外界信号，输出层则是一个 MP 神经元（即阈值逻辑单元）。

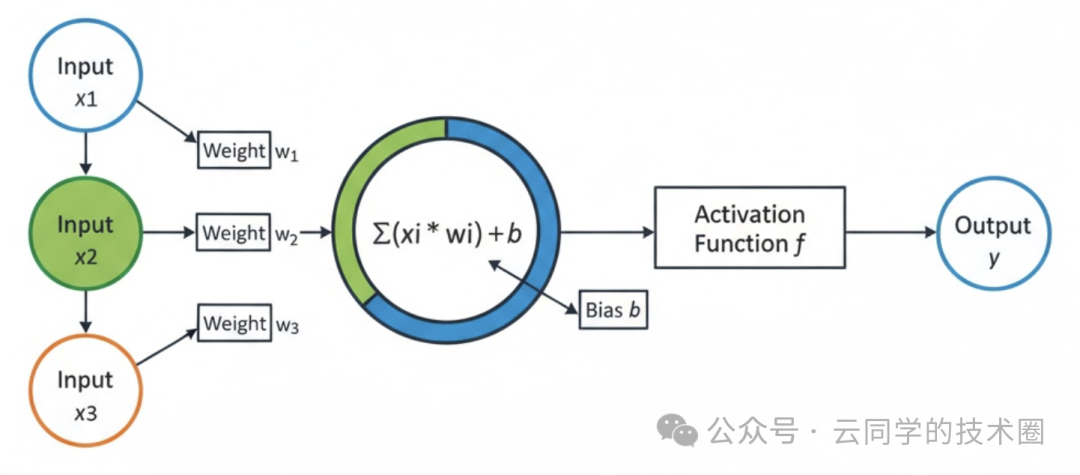
每个输入信号（特征）都会乘以一个对应的权重，然后送入 MP 神经元。神经元将所有加权后的输入求和，再通过一个激活函数（通常是符号函数）映射为最终的分类输出。

02 感知器在解决什么问题？

用一句话概括感知器的工作：对输入进行加权求和，然后判断这个和是否超过某个阈值。

举个例子，假设我们要构建一个网关/限流系统，需要对每个进入的请求快速判断其是否可疑。这本质上是一个二分类问题：

• 输出 1：可疑请求（执行拦截）
• 输出 0：正常请求（执行放行）

我们可以选取三个常见的特征进行判断：

1. \(x_1\)：单 IP 地址最近 1 分钟内的请求次数
2. \(x_2\)：请求是否携带异常 Header
3. \(x_3\)：请求 IP 是否命中过往的黑名单

根据经验，我们会给这些特征赋予不同的权重：

• 命中黑名单影响最大，权重应最高。
• Header 异常影响次之。
• 请求次数相对影响较小，权重也应最低。

对于每一个请求，感知器会根据这些权重计算出一个综合分数。

• 分数高：我们认为该请求可疑概率高，予以拦截。
• 分数低：我们认为该请求正常，予以放行。

03 感知器的实现原理

了解了感知器的任务，接下来我们用数学公式来解析其工作原理。

1. 加权求和

给定输入向量：
\[
\mathbf{x} = [x_1, x_2, x_3]
\]
对应权重向量：
\[
\mathbf{w} = [w_1, w_2, w_3]
\]
加权求和并加上偏置 \(b\)，得到计算结果 \(z\)：
\[
z = w_1 x_1 + w_2 x_2 + w_3 x_3 + b
\]
其中：

• \(w_i\)：权重，代表了对应输入特征的重要性。
• \(b\)：偏置，可以理解为模型判断的“基准线”或“最低门槛”。

2. 激活函数（阶跃函数）

感知器是一个二分类模型，其输出层 MP 神经元是一个阈值逻辑单元。这里我们使用最简单的阶跃函数作为激活函数来决定最终输出：
\[
f(z) =
\begin{cases}
1 & \text{if } z \geq 0 \\
0 & \text{if } z < 0
\end{cases}
\]
这意味着：

• 如果加权和 \(z \geq 0\)，则模型判定为正类（输出 1）。
• 否则，判定为负类（输出 0）。

3. 更新权重向量

对权重的更新，是感知器具备“学习”能力的核心。 其学习规则非常直观：不断试错，不断修正。

假设：

• 样本的真实标签是 \(y\)
• 模型的当前预测是 \(\hat{y}\)

那么权重的更新规则如下：
\[
\mathbf{w} \leftarrow \mathbf{w} + \eta (y - \hat{y}) \mathbf{x}
\]
\[
b \leftarrow b + \eta (y - \hat{y})
\]
其中，\(\eta\) 是学习率，一个介于 0 和 1 之间的比例系数，决定了每次修正的幅度大小。

这个过程很像人类纠错：

• 预测对了：权重和偏置保持不变。
• 预测错了：
  • 把正类(\(y=1\))预测成了负类(\(\hat{y}=0\))：说明模型对这个样本“支持”不够，于是增加权重（\(\mathbf{w} + \eta \cdot 1 \cdot \mathbf{x}\)），使其更倾向于输出 1。
  • 把负类(\(y=0\))预测成了正类(\(\hat{y}=1\))：说明模型对这个样本“支持”过度，于是减少权重（\(\mathbf{w} + \eta \cdot (-1) \cdot \mathbf{x}\)），使其更倾向于输出 0。

4. 重复迭代

重复以上步骤（接收输入、计算输出、比对标签、更新权重），直到达到预设的训练次数或模型不再出错。

04 工程实战：拆解感知器计算过程

现在，我们结合上文提到的网关/限流系统例子，完整走一遍感知器的计算流程。

1. 初始化感知器参数

在真实系统中，模型参数通常随机初始化或根据经验设定。假设我们初始化如下：

• 权重系数
  \[
  \mathbf{w} = [0.1, 0.6, 0.9]
  \]
• 偏置
  \[
  b = -0.5
  \]
  初始权重的设定符合我们的经验认知：黑名单命中权重最高(0.9)，Header异常次之(0.6)，请求次数影响最小(0.1)。

2. 一个真实请求进入

假设一个请求的特征为：1分钟内请求5次(\(x_1=5\))，Header异常(\(x_2=1\))，未命中黑名单(\(x_3=0\))。

用向量表示输入：
\[
\mathbf{x} = [5, 1, 0]
\]

3. 加权求和

带入公式 \(z = w_1 x_1 + w_2 x_2 + w_3 x_3 + b\)：
\[
z = (0.1 \times 5) + (0.6 \times 1) + (0.9 \times 0) + (-0.5) = 0.5 + 0.6 + 0 - 0.5 = 0.6
\]

4. 激活函数判断

使用阶跃函数 \(f(z)\)：
因为 \(z = 0.6 \geq 0\)，
所以模型输出 \(\hat{y} = f(0.6) = 1\)。

模型判断：这是一个可疑请求，需要拦截。

5. 验证判断是否正确

假设该请求在真实场景中其实是正常请求，即真实标签 \(y = 0\)。

显然，模型预测错误了（\(\hat{y}=1, y=0\)），因此需要更新参数。

6. 更新权重

回顾更新规则：
\[
\mathbf{w} \leftarrow \mathbf{w} + \eta (y - \hat{y}) \mathbf{x}
\]
\[
b \leftarrow b + \eta (y - \hat{y})
\]
假设学习率 \(\eta = 0.1\)。
计算误差项 \(y - \hat{y} = 0 - 1 = -1\)。

分别更新 \(w_1, w_2, w_3, b\)：
\[
w_1 \leftarrow 0.1 + 0.1 \times (-1) \times 5 = 0.1 - 0.5 = -0.4
\]
\[
w_2 \leftarrow 0.6 + 0.1 \times (-1) \times 1 = 0.6 - 0.1 = 0.5
\]
\[
w_3 \leftarrow 0.9 + 0.1 \times (-1) \times 0 = 0.9 + 0 = 0.9
\]
\[
b \leftarrow -0.5 + 0.1 \times (-1) = -0.5 - 0.1 = -0.6
\]

7. 更新后的模型有何改进？

使用更新后的参数重新计算同一个请求：
\[
z{new} = (-0.4 \times 5) + (0.5 \times 1) + (0.9 \times 0) + (-0.6) = -2.0 + 0.5 + 0 - 0.6 = -2.1
\]
因为 \(z{new} = -2.1 < 0\)，所以新模型的输出 \(\hat{y}_{new} = 0\)。

结果：模型成功纠正了错误，现在判定该请求为正常请求，予以放行。

从权重变化我们也能直观理解模型的“学习”过程：

• 请求次数多导致误判：权重 \(w_1\) 从 0.1 大幅降低至 -0.4，模型学会了“不能仅仅因为请求频繁就判为可疑”。
• Header异常的影响被修正：权重 \(w_2\) 从 0.6 小幅降低至 0.5，模型明白了“Header异常有嫌疑，但不该一票否决”。
• 黑名单未命中：权重 \(w_3\) 保持 0.9 不变。

本质上，模型通过这次学习告诉自己：“以后判断标准别这么敏感了”。

05 结语：向鼻祖致敬

感知器模型虽然结构简单，功能有限，但它确立了现代深度学习最核心的三大基石：权重、激活函数与误差反向修正。

当我们惊叹于 Sora 生成的逼真视频、或是与 ChatGPT 流畅对话时，不应忘记，在 1957 年，那个名为“感知器”的简单模型，第一次尝试以数学和代码的形式模拟神经元的运作。正是这份跨越半个多世纪的传承与演进，让我们得以站在巨人的肩膀上，见证人工智能以排山倒海之势拓展人类认知与创造的边界。