如何构建基于基本面与深度强化学习的量化交易系统：FNN选股与PPO-CTCN调仓实战

引言

传统的Markowitz均值-方差（MV）模型为投资组合选择提供了基础框架，但其对风险和收益估计的高度敏感性，往往限制了模型的样本外表现。随着机器学习（ML）的发展，其强大的环境适应能力和非线性关系处理能力，为量化金融领域带来了崭新的机遇。本研究提出了一种融合基本面分析与深度强化学习（DRL）的两阶段投资组合管理系统。

该系统首先利用前馈神经网络（FNN）基于基本面数据进行季度股票初筛，随后使用基于时间卷积网络（TCN）的DRL模型进行周度仓位优化。这种混合架构旨在解决传统DRL模型在金融场景中可解释性不足的问题，同时通过创新的奖励函数设计（引入相对等权重组合的超额收益）与主动风险控制机制（湍流指数），使得系统在扣除真实交易成本后，依然能显著跑赢S&P 100指数及多个传统基准策略。

文献综述

股票选择方法

股票选择主要分为基本面分析和技术面分析。前者关注公司的内在价值与长期趋势，后者则侧重于价格与交易量的历史模式。机器学习在此领域应用广泛，支持向量机（SVM）、遗传算法（GA）以及各类神经网络（如FNN、RNN）已被大量研究证明，在预测股价趋势和识别高收益股票方面，其表现通常优于传统统计方法。

投资组合管理方法

现有的基于机器学习的投资组合管理方法大致可归为三类：

1. 无监督学习： 如主成分分析（PCA）和自动编码器，常用于数据降维、噪声过滤和特征提取，但在处理复杂的非线性金融关系时存在明显局限。
2. 监督学习： 如长短期记忆网络（LSTM），通过预测未来资产价格来指导权重分配。这类方法容易过度依赖历史数据分布，且在平衡长期与短期依赖关系上面临挑战。
3. 强化学习（RL）： 智能体通过与环境交互试错来学习最优策略。从早期的Q-learning到如今的深度强化学习（DRL），RL已经能够有效处理连续的状态和动作空间。然而，现有的DRL应用多集中于单纯的选股或权重优化，少有研究能将基本面驱动的股票筛选与动态资产配置有机结合为一个统一的端到端系统。

背景与数学形式化

3.1 基本假设

为确保回测的严谨性与现实适用性，我们建立了以下核心假设：

1. 所有买卖订单均在交易日开盘时按当日开盘价成功执行，确保投资组合在每个交易日开市时能够被精确地重新平衡至目标权重。
2. 智能体（Agent）的交易行为对市场价格不产生影响（即假设交易量相对于整个市场而言微乎其微）。
3. 投资组合禁止使用融资融券和进行卖空操作，始终保持非负持仓，以构建一个稳健、风险可控的投资组合。

3.2 投资组合形式化

一个投资组合由 (N) 只风险资产和现金组成。

• 价格向量： 定义 (\mathbf{p}_t^o) 和 (\mathbf{p}_t^c) 分别为第 (t) 日的开盘价向量和收盘价向量。现金被视为第0项资产，其价格恒为1。
• 收益向量： 资产在第 (t) 日的收益率向量 (\mathbf{y}_t) 定义为 (\mathbf{p}_t^c) 与 (\mathbf{p}_t^o) 的逐元素相除，即 (\mathbf{y}_t = \mathbf{p}_t^c \oslash \mathbf{p}_t^o)。
• 权重向量： (\mathbf{w}t) 表示第 (t) 日开盘时的资产配置权重，需满足 (\sum{i=0}^{N} w{t,i} = 1) 且 (w{t,i} \ge 0)。

由于市场价格波动，第 (t) 日收盘时的权重 (\hat{\mathbf{w}}_t) 会偏离初始权重 (\mathbf{w}_t)。其关系为 (\hat{\mathbf{w}}_t = (\mathbf{y}_t \odot \mathbf{w}_t) / (\mathbf{y}_t \cdot \mathbf{w}_t))。那么，第 (t+1) 日开盘前的权重演变为 (\tilde{\mathbf{w}}_t = \hat{\mathbf{w}}t / \sum{i=0}^{N} \hat{w}_{t,i})。智能体的任务就是在第 (t+1) 日开盘时，将权重从 (\tilde{\mathbf{w}}t) 调整到新的目标权重 (\mathbf{w}{t+1})。

交易成本与投资组合价值： 权重调整会产生交易成本。设定单边交易佣金率 (c)（本文设定为0.2%）。投资组合价值折算因子 (\mu_t) 可表示为：
[
\mut = 1 - c \times \sum{i=1}^{N} |w{t+1,i} - \tilde{w}{t,i}|
]
注意，现金（(i=0)）权重的变化不计入交易损耗。 调整权重后，第 (t+1) 日开盘时的投资组合价值 (v_{t+1}) 及其对数收益率 (rt) 分别为：
[
v{t+1} = v_t \times \mu_t \times (\mathbf{y}_t \cdot \mathbf{w}_t), \quad r_t = \ln(\mu_t \times (\mathbf{y}_t \cdot \mathbf{w}_t))
]
系统的最终优化目标是最大化整个回测期末的投资组合价值 (v_T)。

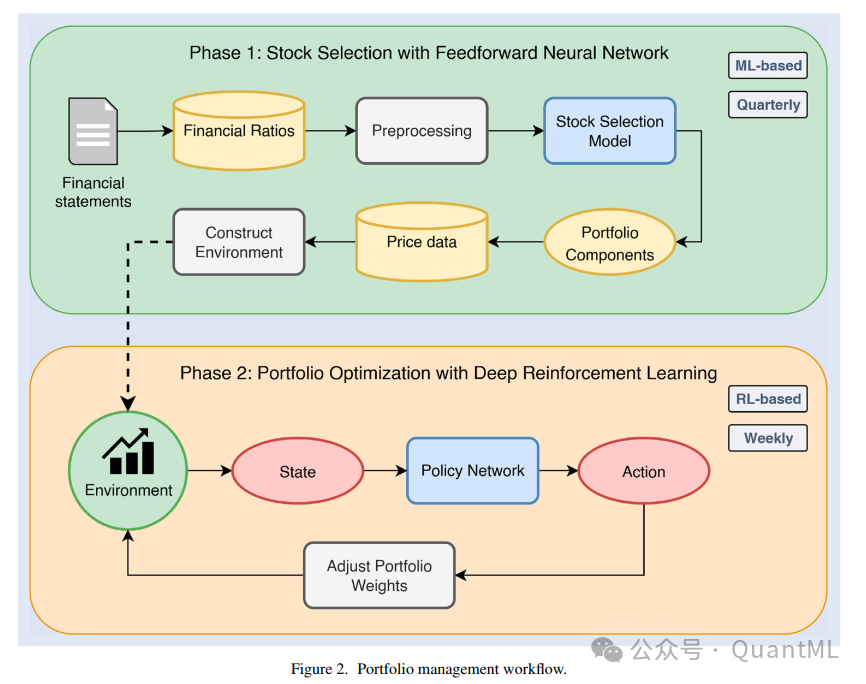
方法论

我们提出的框架包含两个核心阶段：季度股票选择和每日投资组合优化。

4.1 数据集与滚动窗口

研究采用S&P 100指数成分股，数据区间覆盖2009年第一季度至2021年第四季度。数据源包括来自Macrotrends的季度财务报表比率，以及来自Yahoo Finance的日度价格数据。

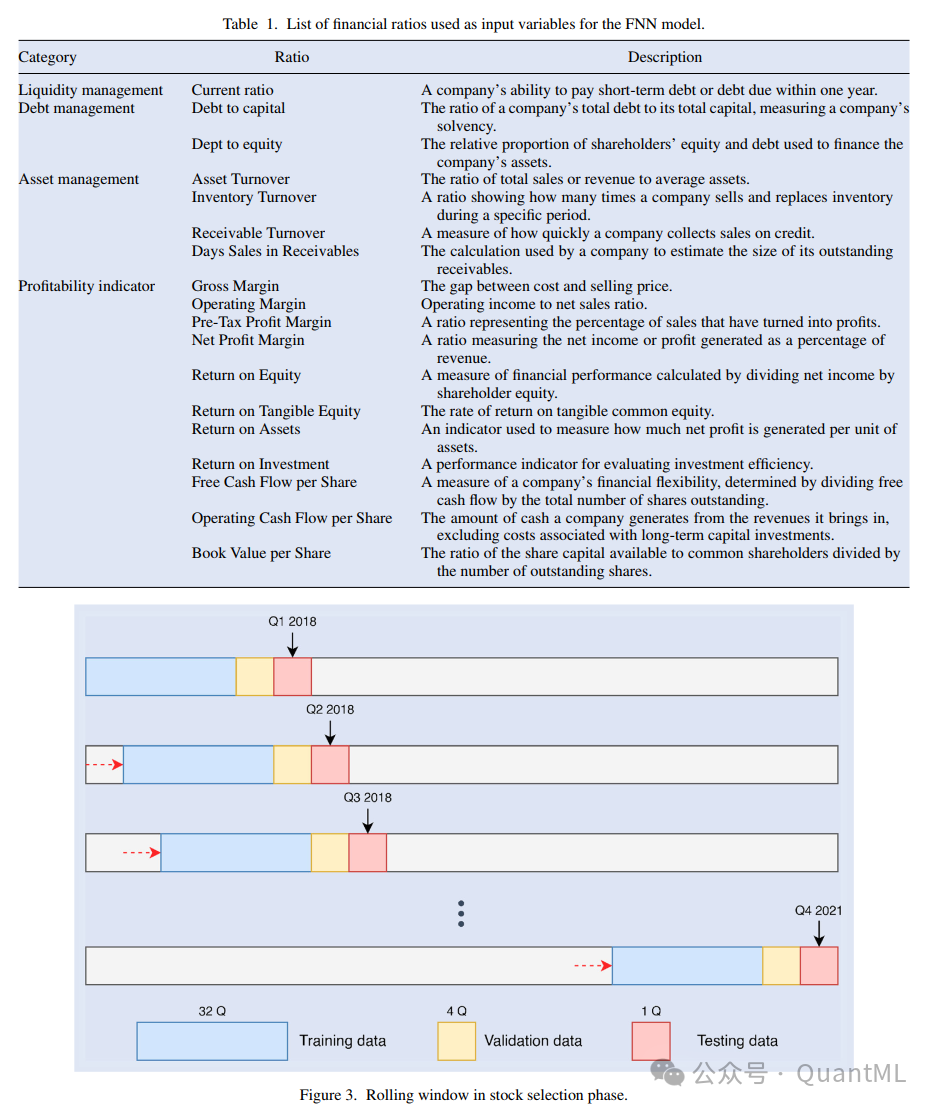
为应对市场环境的动态变化，我们采用滚动窗口（Rolling Window）技术：

• 股票选择阶段： 使用一个包含32个季度的训练窗口，4个季度的验证窗口和1个季度的测试窗口。例如，为了预测2018年第一季度的成分股表现，我们使用2009年第一季度至2016年第四季度的数据进行模型训练。
• 投资组合优化阶段： 考虑到市场波动特性，采用一个长度为3年的固定训练窗口，其后接1个季度的测试窗口和1个季度的模拟交易期。智能体在每个季度末会根据最新的日度价格数据重新进行训练。

4.2 第一阶段：基于FNN的股票选择

我们利用前馈神经网络（FNN）处理上一个季度的财务比率数据，从而筛选出基本面健康、有潜力的股票。

• 输入特征： 涵盖流动性管理、债务管理、资产管理和盈利能力四大类别的18个核心财务比率（如流动比率、资产周转率、净资产收益率ROE等），并增加了基于行业分类的10个虚拟变量。
• 数据预处理： 对缺失值采用均值填充，并对所有特征进行标准化处理。
• 模型架构与优化： 通过网格搜索（Grid Search）优化超参数。最终确定的最优模型结构包含两个隐藏层（节点数分别为30和15），使用Sigmoid激活函数，采用Adam优化器，学习率设为 (10^{-3})。
• 输出与排序： 模型预测的是每只股票相对于S&P 100指数整体的季度相对收益率。根据预测值对所有股票进行降序排名，选取排名前20的股票构建下一阶段的投资组合资产池。该股票池在每个季度末会根据最新发布的财报重新进行排名和更新。

4.3 第二阶段：基于DRL的投资组合优化

在获得由20只优质股票构成的资产池后，DRL智能体负责在其中进行动态的权重分配。

4.3.1 环境构建

环境状态 (\mathbf{s}_t) 是一个形状为 ([N+1, H, 4]) 的张量，它包含了资产在过去 (H) 天内的开盘价、最高价、最低价、收盘价（OHLC）信息，并经过归一化处理以反映价格趋势而非绝对值。现金的“价格”信息也被编码进状态张量。智能体根据当前状态 (\mathbf{s}_t) 输出动作 (\mathbf{a}t)，即新的投资组合权重 (\mathbf{w}{t+1})。

4.3.2 奖励函数设计

为了引导智能体学习能够持续战胜市场的策略，奖励函数 (R_t) 在对数收益率 (r_t) 的基础上，创新性地引入了相对于等权重（EW）组合的超额收益项：
[
R_t = r_t + \lambda (r_t - r_t^{EW})
]
其中 (\lambda) 为超参数，(r_t^{EW}) 为等权重投资组合的日对数收益率。这个设计鼓励智能体在市场基准（EW组合）表现不佳时采取更为保守的策略，而当自身策略表现优于基准时，则能获得更高的正向奖励。

4.3.3 策略网络：CTCN-typed EIIE

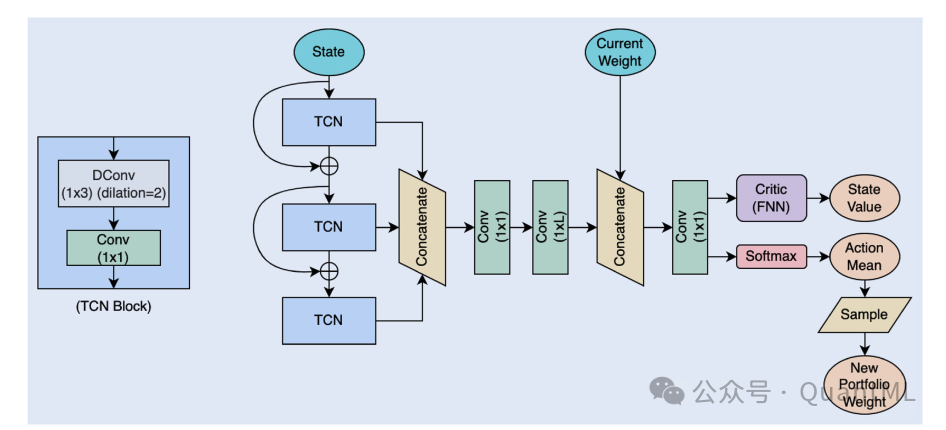
针对金融时间序列数据的特性，本研究改进了经典的EIIE框架，提出了 CTCN-typed EIIE 网络结构。

• 结构优势： 相比传统卷积神经网络（CNN），时间卷积网络（TCN） 引入了因果卷积和空洞卷积。
  • 因果卷积 确保了网络在处理时间序列时，未来信息不会泄露到当前计算中。
  • 空洞卷积 允许网络在不显著增加参数量的前提下，拥有更大的感受野，从而能够有效捕捉更长历史窗口下的价格模式。
• 网络流程： 输入的状态数据依次通过三个带有跳跃连接的TCN模块，以提取不同层级的时间序列特征。这些特征图被拼接后，再经过标准的CNN层进行融合。最后，网络将融合后的特征与当前的持仓权重相结合，通过Softmax层输出新的、归一化的资产权重分配。

4.3.4 算法选择

研究对比了三种主流的深度强化学习算法：

1. PPO (近端策略优化)： 通过Clip函数限制策略的更新幅度，在保证训练稳定性和避免策略崩溃方面表现突出。
2. SAC (柔性演员-评论家算法)： 在目标函数中引入了熵正则化项，鼓励智能体进行更多探索，有助于避免陷入局部最优解。
3. DDPG (深度确定性策略梯度)： 一种适用于连续动作空间的异策略（off-policy）算法。

4.3.5 风险控制：湍流指数

为了应对突发的系统性风险（如战争、疫情引发的市场崩盘），我们引入了湍流指数作为风险控制开关。
湍流指数 (d_t) 的计算公式为：
[
d_t = (\mathbf{r}_t - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\mathbf{r}_t - \boldsymbol{\mu})
]
其中 (\mathbf{r}_t) 是当日所有资产的收益率向量，(\boldsymbol{\mu}) 和 (\boldsymbol{\Sigma}) 是基于历史滚动窗口计算出的收益率均值和协方差矩阵。当 (d_t) 超过预设阈值（本文设定为140）时，判定市场处于极端动荡期，智能体将在次日开盘时卖出所有股票，100%持有现金，直至湍流指数回落至阈值以下，再重新进入市场。

实验与结果分析

实验回测区间为2018年第一季度至2021年第四季度，涵盖了中美贸易战和COVID-19疫情引发的多次市场动荡。评估指标包括累计投资组合价值（APV）、年化收益率（AR）、夏普比率（SR）、索提诺比率（StR）、最大回撤（MDD）和卡玛比率（CR）。

5.1 股票选择模拟结果

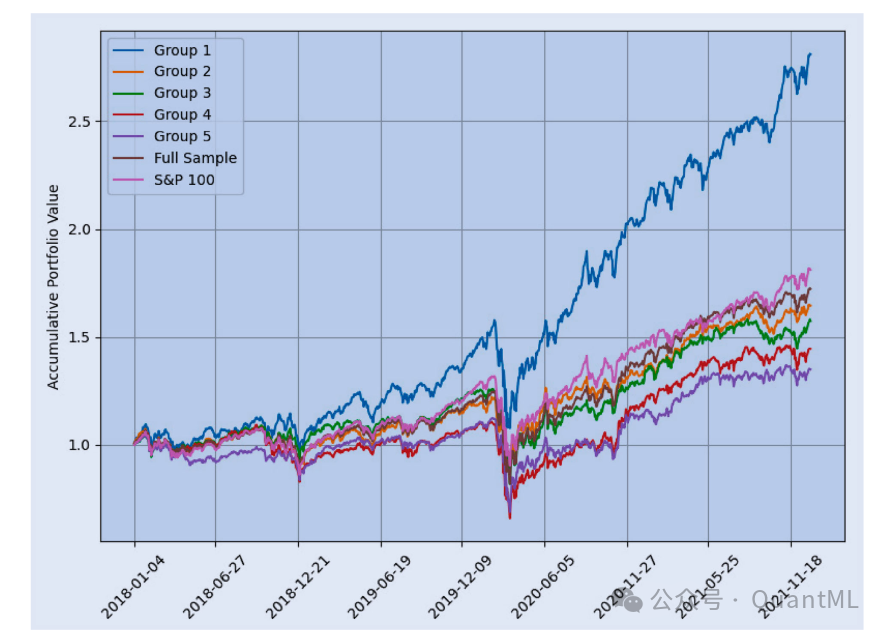
我们将所有股票根据FNN模型的预测排名分为5组（每组约20只股票），并为每组构建简单的等权重组合。

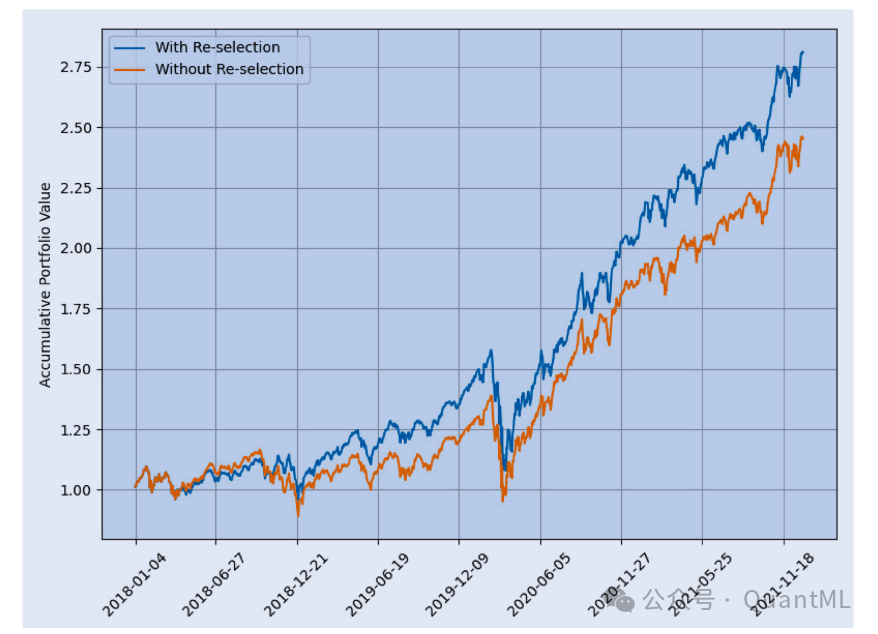
• Group 1（排名前20）表现最优： 无论是否包含后续的季度再选择机制，Group 1组合的表现都显著优于其他分组以及S&P 100基准指数。
• 季度再选择的重要性： 包含季度再选择机制的Group 1组合，其APV达到2.810，SR为1.206；如果锁定在2018年第一季度的初始组合不再更新，APV会下降至2.452，SR降至1.045。这有力地证明了根据最新财报动态调整成分股的必要性。

5.2 投资组合优化模拟结果

5.2.1 优化频率的影响

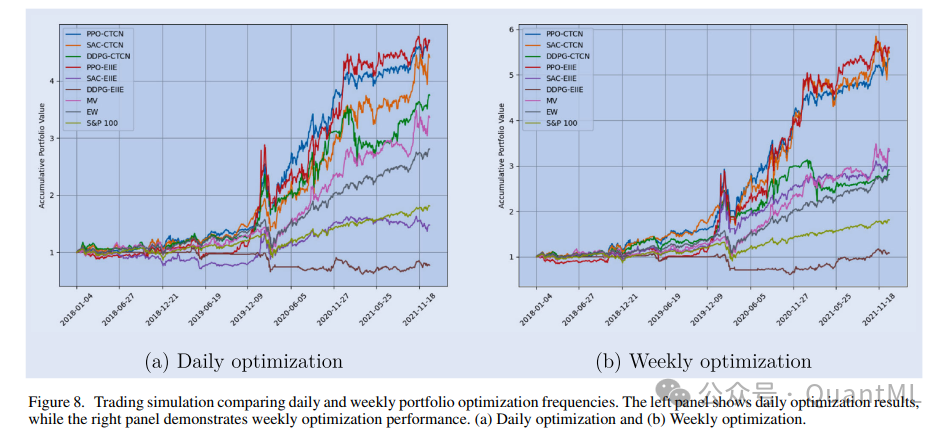
我们对比了每日、周度（5天）、双周（10天）和月度（20天）四种不同的调仓频率：

• 周度优化效果最佳： 在考虑真实交易成本的情况下，5天（周度） 的优化频率实现了最高的APV（5.354）和年化收益率（0.521）。
• 高频交易的弊端： 每日调仓产生了过高的交易成本，并且即便在不考虑成本的情况下，其效果也不如周度调仓。这表明高频的市场噪声可能误导模型，导致其过度拟合短期波动。

5.2.2 算法与网络性能对比

在周度优化的设定下，我们对比了不同DRL算法（PPO, SAC, DDPG）与不同网络架构（CTCN, 传统CNN-EIIE）的组合表现：

• PPO-CTCN表现最为均衡稳健： 虽然SAC-CTCN在忽略交易成本的理想环境下表现强劲，但在综合考虑成本和风险调整后，PPO-CTCN展现了极佳的稳定性，尤其是在穿越不同的市场周期时。
• CTCN架构显著优于传统CNN： 无论是搭配PPO、SAC还是DDPG算法，采用CTCN架构的变体在APV和SR上均一致优于采用传统CNN（EIIE）架构的变体。这证实了TCN在处理长序列金融数据特征提取方面的天然优势。
• SAC算法的特点： SAC-CTCN取得了最高的风险调整后回报（卡玛比率CR为1.988），这得益于其熵正则化带来的充分探索，使其能在减少不必要的交易频率的同时，捕捉到高确定性的机会。但其在2015-2017年样本外测试期的表现不如PPO稳定。

5.2.3 选股对优化的重要性（Group 2分析）

我们将同样的PPO-CTCN优化算法应用于排名第21至40名的股票（Group 2）：

• 结果显示，即便使用最先进的DRL优化算法，Group 2投资组合的最终表现（APV 1.644）也远远逊色于Group 1的简单等权重持有组合（APV 2.810）。
• 核心结论： 优质的股票选择是投资组合长期优异表现的基石。单纯依靠复杂的权重优化算法，无法弥补底层资产质量的平庸。

5.3 鲁棒性检验

5.3.1 不同时间段的测试

我们对比了模型在2015-2017年（相对平稳/牛市）和2018-2021年（高波动）两个不同市场时期的表现：

• PPO-CTCN表现出一致性： 在两个差异显著的时期，PPO-CTCN均保持了较高的夏普比率（分别为1.519和1.53），证明了其对不同市场机制具有强大的适应能力。
• SAC存在不稳定性： SAC-CTCN在2015-2017年期间的表现出现大幅下滑（SR仅为0.687），存在过拟合特定市场环境（如2018-2021高波动期）的风险。

5.3.2 信息发布时间错配测试

我们测试了如果延迟到季度中期才根据已发布的财报调整股票成分池（模拟信息获取或处理延迟）：

• 结果显示系统性能出现显著下降。PPO-CTCN的APV下降了51.3%。
• 这强调了信息时效性的极端重要性：在财报发布后立即调整仓位，能够有效捕获市场对基本面新信息的初步反应，推迟操作会错失趋势形成的关键窗口期。

5.4 奖励函数与湍流指数评估

• 奖励函数参数 (\lambda)： 当设置 (\lambda = 1)（即引入相对EW收益项）时，系统的APV比 (\lambda = 0)（仅使用绝对收益）时提高了59.6%。这表明将市场平均水平作为基准（Anchor）能有效指导智能体学习更稳健、更具竞争力的策略。
• 湍流指数的风控效果： 引入湍流指数风控后，在2020年第一季度（COVID-19爆发期）成功帮助系统规避了市场最猛烈的下跌。最大回撤（MDD）从49.8%降低至35.6%，亏损减少了14.2个百分点，最终的APV也因此提升了47.3%。

5.5 完整系统综合评估

我们将“FNN选股 + PPO-CTCN周度优化 + 湍流指数风控”作为一个完整的系统进行综合评估：

• 完整系统 vs. 仅选股： 完整系统的APV高达5.354，而仅进行FNN选股并等权重持有的APV为2.810。
• 完整系统 vs. 仅优化： 如果跳过选股阶段，直接对S&P 100全样本股票使用PPO-CTCN进行优化，仅能获得1.883的APV。
• 协同效应： 第一阶段的选股提供了高质量、低噪声的资产池，为第二阶段的优化奠定了坚实基础；第二阶段的动态优化则进一步利用价格波动和趋势增强了收益。两者的结合产生了显著的“1+1>2”的协同效应，最终夏普比率达到1.53，远超S&P 100指数的0.765。

讨论

实验结果不仅验证了所提出模型的盈利能力，更体现了其在金融逻辑上的高度可解释性。FNN基于财务比率筛选出的股票，即使采用最简单的等权重持有策略，也能持续跑赢大盘，这本身就证明了所选基本面因子的长期有效性。而季度再选择机制则确保了投资组合始终由当前财务状况最健康的公司构成，实现了动态的“优胜劣汰”。

CTCN网络结构的引入，显著提升了模型对金融时间序列特征的提取效率。相比之下，传统的CNN结构在处理这种具有长期依赖关系的序列数据时显得力不从心。PPO算法配合CTCN网络展现出的跨周期稳定性，使其成为实际投资组合管理应用中最可靠的选择。尽管SAC在特定时期能斩获更高收益，但其业绩表现的较大波动性，可能让风险厌恶型的投资者或机构难以接受。

此外，研究中的一个关键发现是：单纯依赖DRL对全样本股票进行优化，其效果非常有限（仅略好于S&P 100指数）。这是因为全样本中包含大量基本面不佳或股价表现羸弱的股票，这些“噪音”资产严重干扰了智能体的学习过程，导致资金被错误地配置到高风险、低回报的资产中。这一结果从反面强有力地论证了第一阶段进行基本面预筛选的不可或缺性。

结论

本研究成功设计并验证了一个深度融合基本面分析与深度强化学习的端到端量化投资组合管理系统。

1. 核心贡献： 提出了一种创新性的两阶段框架，将前馈神经网络（FNN）用于季度股票初选，并结合改进的PPO-CTCN算法进行周度动态仓位优化。
2. 性能验证： 该系统在回测中展现出卓越的性能，在绝对收益率、风险控制（夏普比率、最大回撤）和跨周期稳定性方面，全面超越了传统的均值-方差模型、等权重模型以及S&P 100市场基准。
3. 关键发现：
   • 股票选择对最终组合表现的贡献权重巨大，优质的资产池是成功的前提。
   • 周度调仓频率在有效捕捉市场趋势与控制交易成本之间取得了最佳平衡。
   • 引入相对收益基准的奖励函数和基于湍流指数的主动风控机制，极大地增强了模型在真实市场环境中的实战能力和鲁棒性。

这项研究为量化投资从业者及研究者提供了一个兼具金融逻辑可解释性与高性能的端到端投资组合管理新范式。对这类人工智能在金融领域的深度应用感兴趣的开发者，可以持续关注云栈社区的相关技术讨论与分享。