在算法交易 (Algorithmic Trading) 与交易成本分析 (TCA) 中,准确的成交量预测 (Volume Prediction) 是控制市场冲击成本 (Market Impact) 的核心输入。无论是 VWAP 策略的执行路径规划,还是实施缺口 (Implementation Shortfall) 策略的参数设定,都高度依赖于对全天总成交量 (Total Daily Volume) 及日内分布 (Intraday Profile) 的精准估计。
金融数据固有的非平稳性、低信噪比以及“肥尾”特征,使得单一的时间序列模型难以在所有场景下表现优异。本文将介绍一种被称为“五重奏 (Quintet)”的集成框架。该框架不依赖单一黑箱,而是将预测任务解耦为五个协同工作的子模型,并利用贝叶斯推断 (Bayesian Inference) 机制,在盘中实时更新预测。
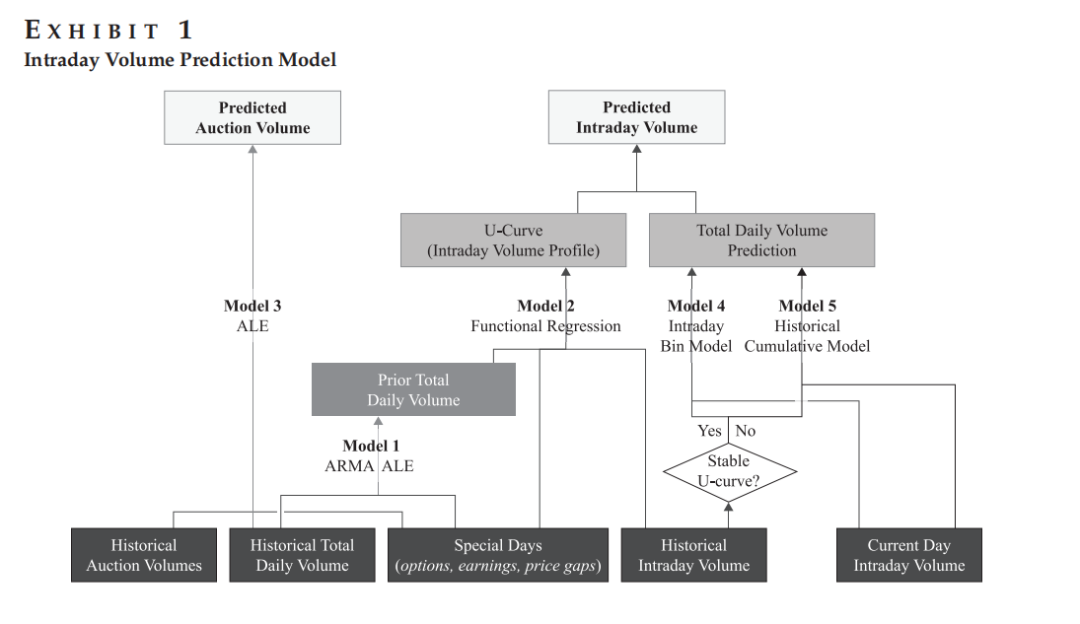
Figure 1 展示模型的整体架构,包括日历史先验、日内U型曲线、以及分别针对流动性好坏标的的贝叶斯更新模块。
2. 核心数学假设与变量定义
2.1 对数正态分布假设
金融资产的成交量 V 必须为正且通常呈现显著的右偏分布。为了利用高斯分布的优良性质,我们引入对数正态分布假设。
假设 1: (Log-Normal Distribution) 假设某一时段的成交量 V 服从对数正态分布,即其对数 v = log(V) 服从正态分布:
v ∼ N(μ, σ²)
其中 μ 为对数均值,σ 为对数标准差。这一假设是后续构建共轭先验的基础。
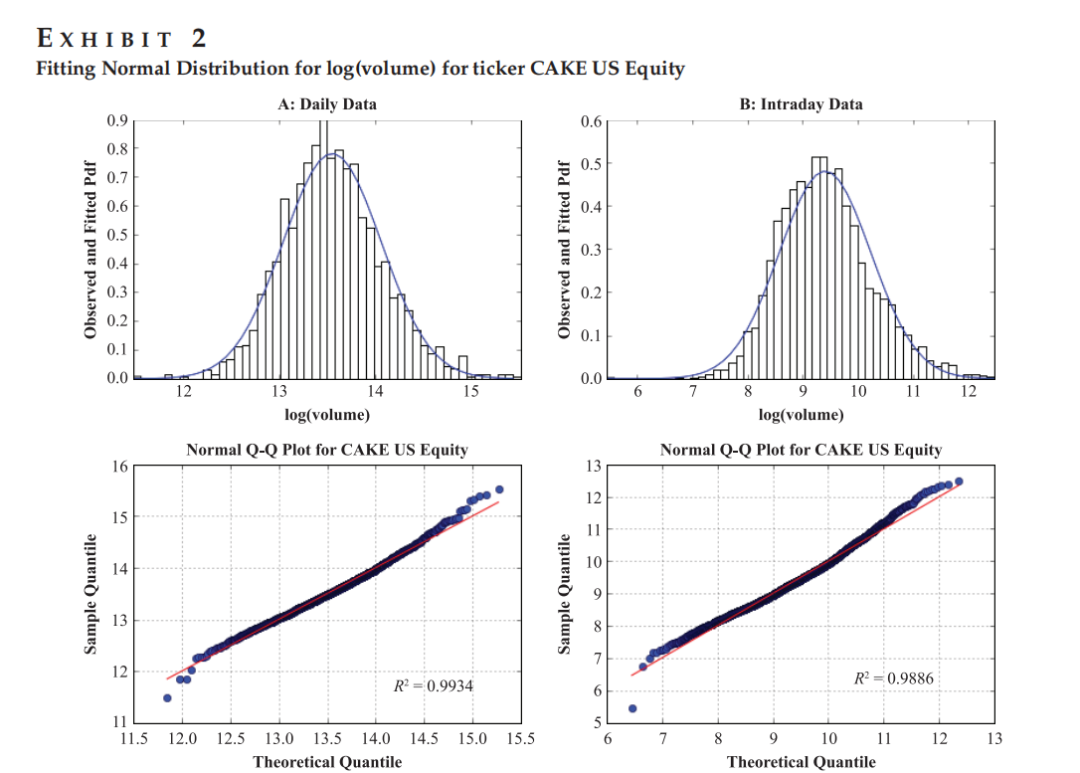
Figure 2 说明对数变换后的日成交量和日内Bin成交量呈现良好的正态分布特性(Q-Q图拟合),验证了假设的有效性。
2.2 非对称对数误差 (ALE)
在交易执行中,风险是不对称的。高估流动性会导致算法设置过高的参与率,从而产生巨大的市场冲击成本;而低估流动性仅导致执行速度稍慢,风险相对可控。因此,模型训练的目标函数应惩罚高估误差。
定义 1: (Asymmetric Logarithmic Error, ALE)
ALE(V_pred, V_act) = w(e) * (log(V_pred) - log(V_act))²
其中权重函数 w(e) 定义为:
w(e) = { 2, if V_pred > V_act (Overestimation)
1, if V_pred <= V_act (Underestimation) }
这意味着高估成交量的惩罚权重是低估的两倍,迫使模型给出更保守的预测。
3. 数学推导:贝叶斯更新机制
本框架的核心在于利用盘中已实现的成交量 (Likelihood) 去更新盘前对全天成交量的先验估计 (Prior)。
3.1 场景一:已知方差下的均值推断
对于流动性较好的股票,日内波动率 σ 相对稳定,可视为已知量。我们需要利用日内观测数据 v_1, ..., v_t 推断全天成交量均值 μ。
定理 1: (Normal-Normal Conjugacy) 设观测数据 v_i 独立同分布于 N(μ, σ²),其中 σ² 已知。若均值 μ 的先验分布为 N(μ_0, σ_0²),则其后验分布 P(μ|v_1,...,v_t) 仍为正态分布 N(μ_n, σ_n²),且参数满足:
μ_n = (1/σ_0² * μ_0 + t/σ² * v̄_t) / (1/σ_0² + t/σ²)
σ_n² = 1 / (1/σ_0² + t/σ²)
其中 v̄_t 为当前观测均值。
证明: 根据贝叶斯定理 P(μ|data) ∝ P(data|μ) * P(μ)。 似然函数项:
P(data|μ) ∝ exp[ -1/(2σ²) * Σ_i (v_i - μ)² ]
先验分布项:
P(μ) ∝ exp[ -1/(2σ_0²) * (μ - μ_0)² ]
考察指数部分的核:
-1/2 * [ (1/σ_0²)(μ - μ_0)² + (1/σ²) Σ_i (v_i - μ)² ]
展开关于 μ 的二次项并配方 (Completing the square):
∝ -1/(2σ_n²) * (μ - μ_n)²
令后验精度 1/σ_n² = 1/σ_0² + t/σ²,并对比标准正态分布指数形式 -(μ - μ_n)²/(2σ_n²),解出 μ_n 即得证。
经济含义:后验均值 μ_n 是先验均值 μ_0 和观测均值 v̄_t 的凸组合。权重取决于各自的“精度”(Precision,方差的倒数)。随着交易进行 (t 增加),先验的影响力逐渐减弱,预测值收敛于盘中实时均值。
3.2 场景二:未知均值与未知方差的推断
在开盘初期或针对非流动性标的,方差 σ² 未知。此时需使用 Normal-Gamma 分布作为共轭先验。
定理 2: (Normal-Gamma Inference) 设 μ 和精度 τ = 1/σ² 的联合先验服从 Normal-Gamma 分布 NG(μ_0, κ_0, α_0, β_0)。在观测到 n 个数据后,均值 μ 的边际后验分布 (Marginal Posterior) 为学生t分布 (Student's t-distribution)。其后验均值的点估计 E[μ|data] 为:
μ_n = (κ_0 * μ_0 + n * v̄_n) / (κ_0 + n)
其中 κ_0 代表先验的“有效样本量” (Effective Sample Size)。
证明摘要: 写出联合后验分布 P(μ, τ|data)。利用共轭性质,更新后的参数 κ_n = κ_0 + n。对联合分布关于 τ 积分以消去精度参数,即可得到关于 μ 的t分布,其期望即为上述加权形式。
此公式提供了一个平滑过渡机制:在开盘初期 (n 很小),预测主要依赖先验 μ_0;随着交易进行,预测权重线性地向实时数据 v̄_n 倾斜。通常取 κ_0 = 1。
4. 五重奏模型组件 (The Quintet Model)
该框架将复杂的预测任务解构为五个协同工作的子模型。
4.1 模型 1:日度总成交量先验 (Daily Prior)
作为贝叶斯的起点 μ_0,我们需要基于历史数据构建稳健估计。
- 几何平均 (Geometric Mean):由于对数正态分布,算术平均会高估中位数。
exp( mean(log(V_hist)) ) 是更佳选择。
- ARMA 动态调整:对去趋势后的对数序列 v_t 拟合 ARMA(1,1) 模型,捕捉自相关性(趋势)与均值回归 (Shock Recovery)。
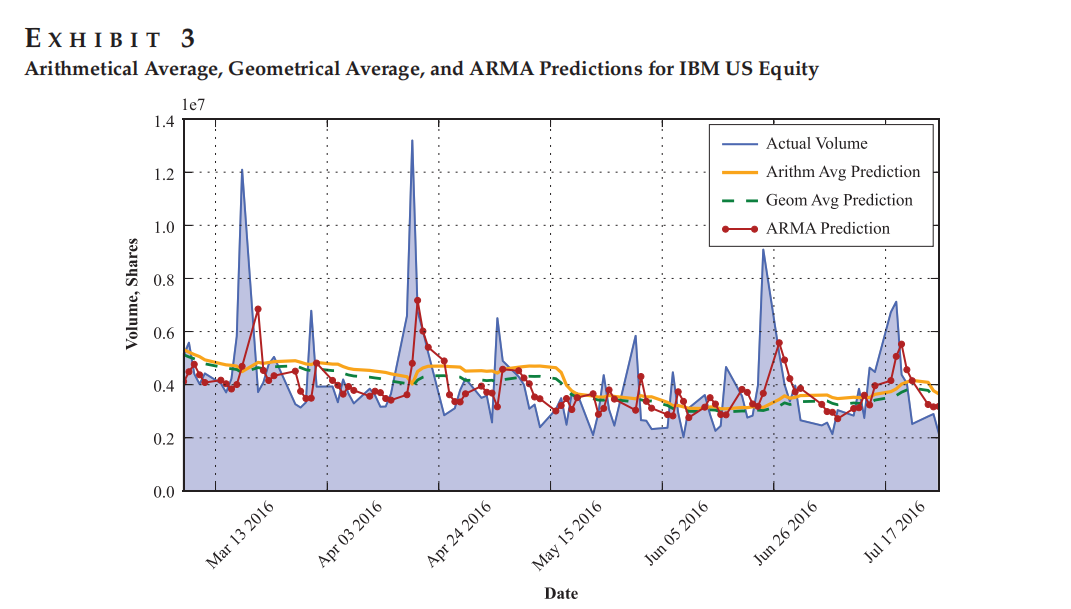
Figure 3展示ARMA模型预测与几何平均、算术平均在捕捉成交量动态变化上的对比。
4.2 模型 2:日内形态 U-Curve (Intraday Profile)
定义 u_t 为第 t 个时间窗成交量占全天比例。研究发现其形状受隔夜价格跳空 (Overnight Gap) 影响显著。
函数型回归: (Functional Regression) 建立累积占比 c(t) 对隔夜缺口 g 的回归:
c(t) = b_0(t) + b_1(t) * g + ε_t
推论: b_1(t) 在开盘初期显著为正。这意味着隔夜跳空越大,早盘成交量占比越高,U型曲线越陡峭(呈倒J型)。
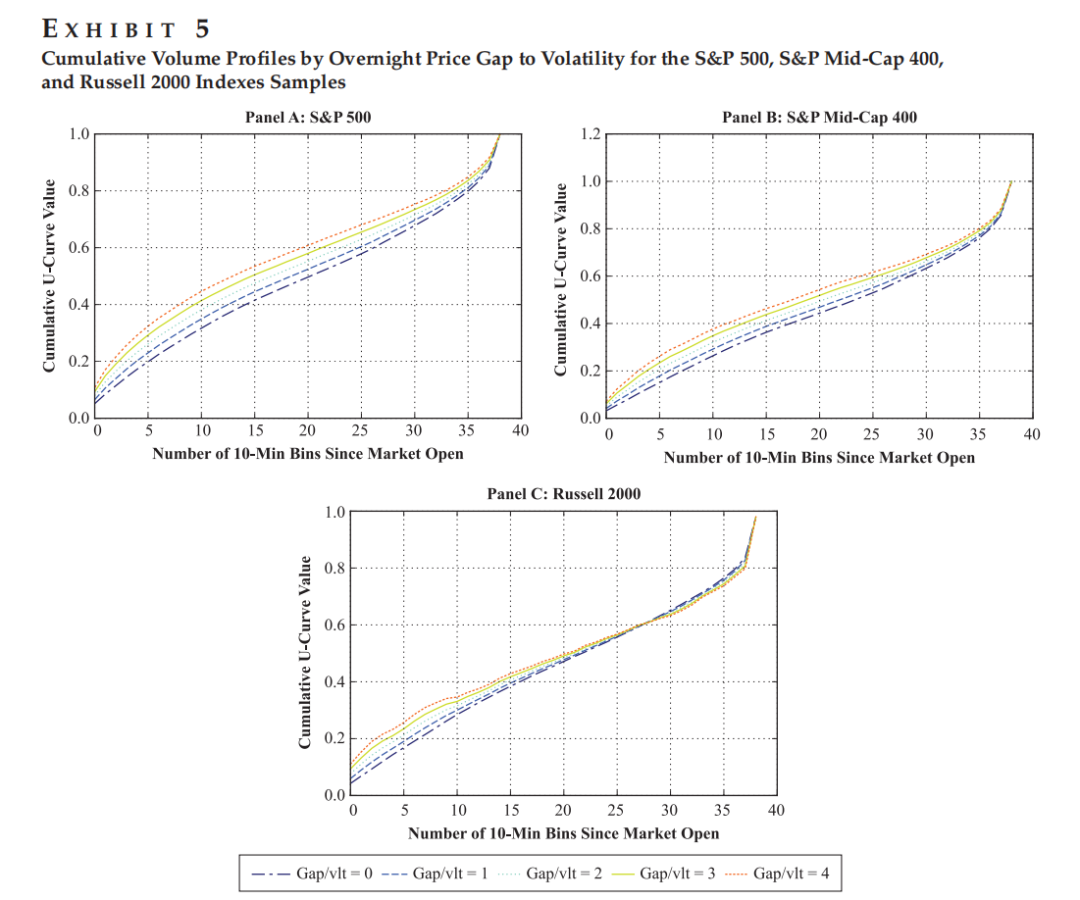
Figure 5 展示不同隔夜跳空幅度下,累积成交量曲线c(t)的显著形态差异。
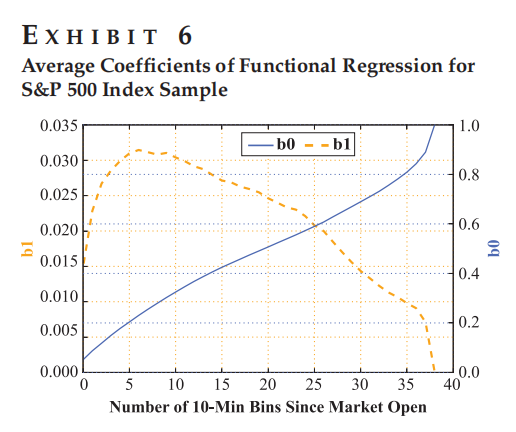
Figure 6 展示函数型回归系数 beta(t) 随时间的变化情况。
4.3 模型 3:收盘集合竞价 (Auction Model)
收盘竞价独立于连续交易。模型采用几何平均作为基准,并叠加期权到期日(如三巫日)的虚拟变量回归:
log(V_auction) = β_0 + β_1 * I_special + ε
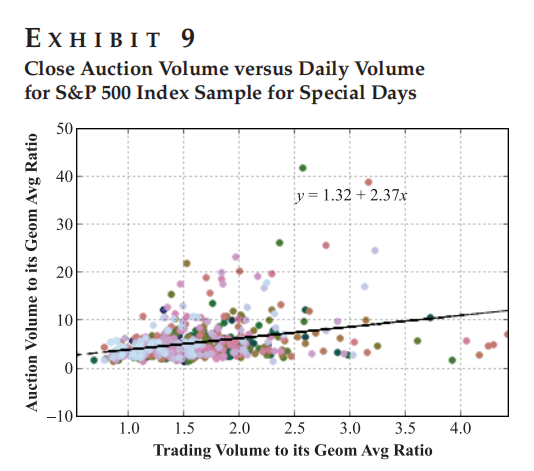
Figure 9 展示特殊日子(如期权到期日)收盘竞价成交量与日均成交量的强回归关系。
4.4 模型 4:日内分桶模型 (Bin Model) —— 针对流动性标的
适用于流动性好的股票。设 v_t 为第 t 个时间窗的实际成交量,u_t 为模型2预测的占比。该Bin隐含的全天对数成交量为:
z_t = v_t - log(u_t)
利用 定理 2,在 n 个Bin之后的更新预测为:
μ_n = (κ_0 * μ_0 + Σ_{i=1}^n z_i) / (κ_0 + n)
4.5 模型 5:历史累积模型 (Cumulative Model) —— 针对非流动性标的
适用于流动性差、存在零成交量Bin的股票。此时单一Bin的估计不稳定。转而使用“截止当前的累积成交量” C_t。构造观测变量:
y_t = C_t - log( U_cum(t) )
其中 U_cum(t) 是模型2预测的截止时间t的累积比例。
利用历史样本中 y_t 的方差 σ_y² 作为权重进行更新(基于定理 1的变体):
μ_t = (1/σ_0² * μ_0 + 1/σ_y² * y_t) / (1/σ_0² + 1/σ_y²)
5. 结论
最终,在时刻 t,剩余需要交易的成交量 V_remaining 为:
V_remaining = exp(μ_t) * (1 - U_cum(t))
该“五重奏”模型通过将复杂问题解构,并利用贝叶斯推断的解析解形式,成功解决了先验与后验的最优融合问题。同时,通过引入ALE误差度量,模型内嵌了对高估流动性风险的防御机制,非常适合买方机构的执行算法需求。
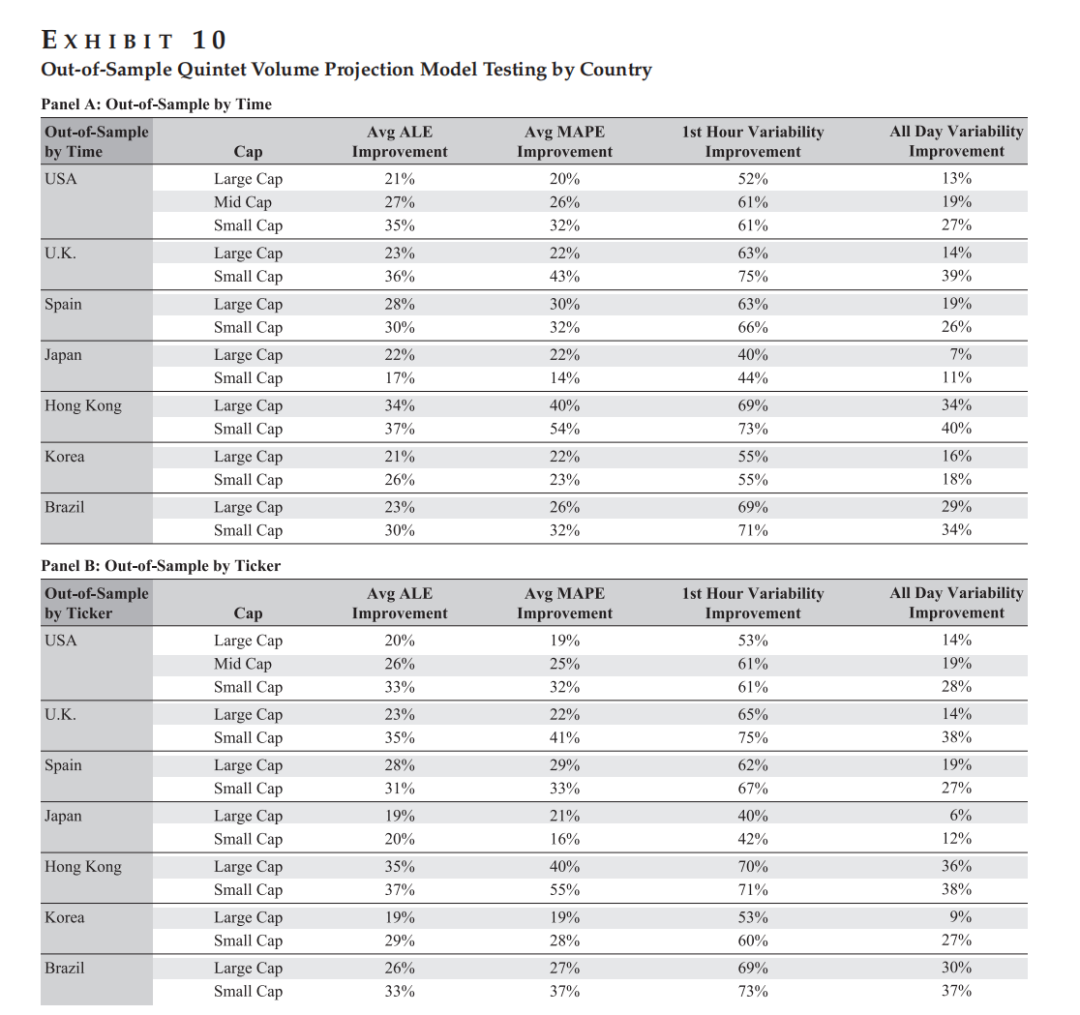
Figure 10 表格说明该模型在样本外测试中相对于传统基准模型在ALE和MAPE指标上的显著改进。
本文详细剖析了将数据挖掘与贝叶斯统计应用于金融预测的具体实践,希望能为相关领域的研究者和开发者提供有价值的参考。更多前沿技术讨论与实战分享,欢迎关注云栈社区。