在上一篇文章概述了RNN如何让机器“读懂”时间后,本篇我们将从数学和计算的角度,深入RNN的循环机制,看看时间是如何被“折叠”进记忆的。
一切的核心:隐藏状态
RNN最核心的概念是隐藏状态,通常记为 $h_t$。你可以把它理解为网络的“短期记忆”。在每个时刻 $t$,RNN并非从头开始,而是:接收当前输入 $x_t$,读取上一步的记忆 $h_{t-1}$,然后将两者融合、更新,得到新的记忆 $h_t$。
关键在于,历史信息是被编码进当前状态里的。RNN并非直接记住原始输入,而是记住一个经过抽象和压缩后的状态表达。
其核心计算过程可以用一个公式来概括:

公式解读:
- $x_t$:当前时刻的输入(例如句子中第 $t$ 个字的词向量)。
- $W_{ih}$:输入权重矩阵,负责处理当前输入。
- $W_{hh}$:循环权重矩阵,负责处理上一步的隐藏状态,是记忆传递的核心。
- $tanh$:激活函数,将数值压缩到 $[-1, 1]$ 之间,防止记忆在循环中无限膨胀或消失。
从结构上看,RNN像一个在自我循环的节点;但从计算视角看,它像是在时间维度上展开的深度网络。实际上,这些“展开层”共用同一套权重 $W_{hh}$,只是在不同的时间点被反复调用。这就引出了RNN高效的关键——参数共享。
精打细算:神奇的参数共享
为什么RNN能高效处理任意长度的序列?答案就在于参数共享。
假设:
- 输入向量维度 $D_{in}$:$x_t$ 的大小(例如词向量维度100)。
- 隐藏层维度 $D_h$:$h_t$ 的大小(例如记忆容量128)。
一个RNN单元需要学习的参数主要包括两组权重矩阵和偏置:
- 输入权重 $W_{ih}$,形状为 $D_h \times D_{in}$。
- 循环权重 $W_{hh}$,形状为 $D_h \times D_h$。
- 偏置 $b_{ih}$ 和 $b_{hh}$:形状均为 $D_h$(通常合并计算)。
因此,RNN的参数量大约为:$D_h \times (D_{in} + D_h + 1)$。
我们来做个横向对比(忽略偏置):
假设 $D_{in}=100$,$D_h=128$。
- FNN(全连接网络):若序列长度为10,FNN需要将序列展平输入($10 \times 100 = 1000$维)。参数量 $\approx 1000 \times 128 = 128,000$。缺点:参数量随序列长度线性爆炸。
- CNN(1D卷积,核大小3):参数量 $\approx 3 \times 100 \times 128 = 38,400$。特点:参数少,但只看局部上下文,与序列全长无关。
- RNN:参数量 $\approx 128 \times (100 + 128) = 29,184$。特点:参数固定且较少,无论序列长10还是长10,000,参数量都保持不变。
RNN正是通过这种参数共享机制,用一套有限的参数去拟合任意长度的时间序列,这是其架构上的巨大优势。
灵活输入:理论上不限长度
由于采用循环处理和参数共享,RNN在架构层面对输入序列长度没有硬性限制。无论你输入10个词还是1000个词,它都是用同一套权重循环跑完整个序列。
当然,这只是理论上的。在实践中,由于著名的“梯度消失/爆炸”问题,普通RNN能有效利用的历史信息非常有限,通常在十几步之后,早期的信息就几乎被遗忘殆尽了。这也正是LSTM和GRU等更复杂序列模型被提出的原因。
与其他模型对比:
- FNN:固定长度(硬限制)。输入层神经元数量是固定的,处理变长序列时需暴力截断或补零,很不灵活。
- Transformer:有长度限制(上下文窗口)。虽然自注意力机制理论上可处理整个序列,但受限于显存和计算复杂度,存在上下文窗口大小约束。输入超长时必须截断或分段。不过,相比RNN,Transformer在其窗口内处理长距离依赖的能力要强得多。
只能串行:RNN的最大瓶颈
RNN最大的痛点,也是其训练缓慢的根本原因:计算必须严格串行。
其数学本质是一个随时间递归的函数:当前隐状态 $h_t$ 是上一个隐状态 $h_{t-1}$ 的函数。
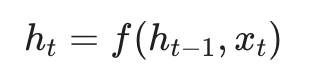
GPU最擅长的是并行计算,希望一次性处理巨大的矩阵。但在RNN中,计算时刻 $t$ 必须等待时刻 $t-1$ 的结果。这导致GPU的大量计算核心在多数时间处于空闲等待状态,无法发挥其并行威力。
你可能会有疑问:“既然权重共享,不能从数学上推导出所有 $h_t$,实现并行吗?”
从数学表达式上看,确实可以。如果没有非线性激活函数,RNN就是线性的(忽略偏置):
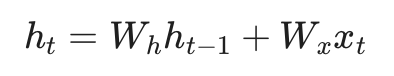
进而可以展开:
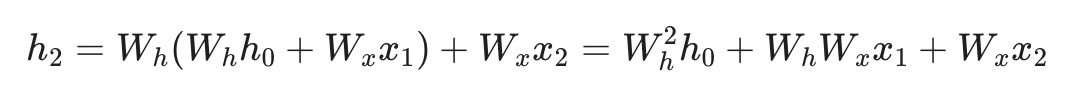
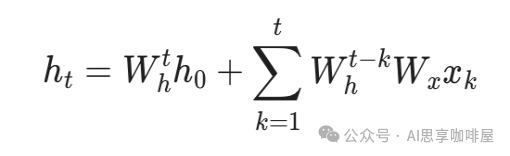
此时,我们可以利用矩阵乘法的结合律,提前计算矩阵的幂,然后一次性算出所有 $h_t$,实现并行。近年来像Mamba等架构,也是通过特定技巧让模型部分回归线性递推,从而实现高效并行。
但现实是,为了拟合复杂模式,RNN每一步都包含非线性激活函数(如 $tanh$),公式变为嵌套结构:
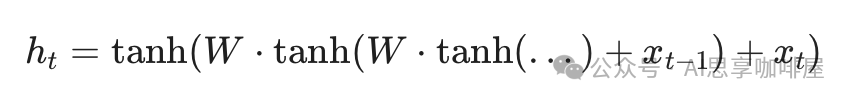
这就如同一个加密的黑盒。要计算外层的 $tanh$,必须先知道内层的具体数值。GPU在执行时,面对的是 $f(f(f(...)))$ 这样的嵌套函数,它无法跳过中间步骤,必须由内向外逐层计算,串行无法避免。
为什么Transformer没有这个问题?
Transformer的自注意力机制是全局且无依赖的。每个输出位置都直接基于所有输入位置进行计算,彼此间没有先后依赖。因此,在训练时它可以充分利用GPU的并行能力。
训练 VS 推理
你可能会问:在推理时,大家不都是“一个字接一个字”地生成吗?
是的,在文本生成这类任务中,无论RNN还是Transformer,生成下一个词都需要依赖上一个词的输出,因此推理过程本质都是串行的。
区别在于文本分类(如情感分析)这类任务:给定完整句子后,RNN依然需要串行计算整个序列,而Transformer可以一次性并行处理整个句子,推理速度更快。
总结来说:
- 训练时:无法并行是RNN的致命伤,导致其在大数据场景下训练效率低下。
- 推理时:在生成任务中所有模型都串行;在理解类任务中,Transformer的并行优势依然明显。
代码示例:用PyTorch理解维度变化
下面通过一个简单的PyTorch示例,直观感受RNN的输入输出维度变化。
import torch
import torch.nn as nn
# 1. 定义数据维度
batch_size = 2 # 一次处理2个句子
seq_len = 5 # 每个句子5个词
input_size = 10 # 每个单词用一个10维向量表示
hidden_size = 20 # 隐藏层记忆容量设为20
# 2. 创建输入数据 (batch_first=True,更符合直觉)
# 形状: [batch_size, seq_len, input_size] -> [2, 5, 10]
input_seq = torch.randn(batch_size, seq_len, input_size)
# 3. 定义RNN层
rnn_layer = nn.RNN(input_size=input_size,
hidden_size=hidden_size,
num_layers=1, # 堆叠RNN层的数量,默认为1
batch_first=True,
nonlinearity='tanh' # 默认激活函数
)
# 4. 前向传播
# output: 包含了每个时间步的输出
# h_n: 只是最后一个时间步的记忆状态
output, h_n = rnn_layer(input_seq)
print("输入尺寸:", input_seq.shape) # torch.Size([2, 5, 10])
print("Output尺寸:", output.shape) # torch.Size([2, 5, 20])
# 解读: [Batch, Seq_Len, Hidden_Size] -> 每个词读完都有一个20维的理解
print("H_n尺寸:", h_n.shape) # torch.Size([1, 2, 20])
# 解读: [Layers, Batch, Hidden_Size] -> 只有最终那个时刻的记忆

通过代码可以看到,RNN就像一个特征转换器,将 input_size 维的输入提升为 hidden_size 维的记忆,并在时间维度上留下了完整的轨迹(output)。
需要注意的是,代码中的 output 是RNN所有时间步的隐藏状态。在实际任务(如分类)中,通常需要在此基础上做进一步处理(例如取最后一个时间步的 output 或 h_n,再接一个全连接层),才能得到最终的预测结果。
总结与展望
今天我们深入剖析了RNN的循环机制。其核心在于通过隐藏状态和参数共享,理论上实现了对任意长度序列的处理。然而,梯度消失问题使其难以有效利用长距离信息,计算上的串行瓶颈也限制了其训练效率。这些缺陷催生了LSTM、GRU等更强大的序列模型。
在云栈社区的后续讨论中,我们将深入探讨LSTM与GRU如何通过精巧的“门控”机制解决长期依赖问题,并比较它们与Transformer中的自注意力机制有何异同。为什么看似简单粗暴的矩阵乘法,最终超越了那些精心设计的门控结构?这背后是深度学习发展史上一次重要的范式转换。
注:本文由AI辅助生成,旨在提供清晰的技术解析。