时域信号净化实战指南：5大核心算法从基线校正到KNN平滑详解

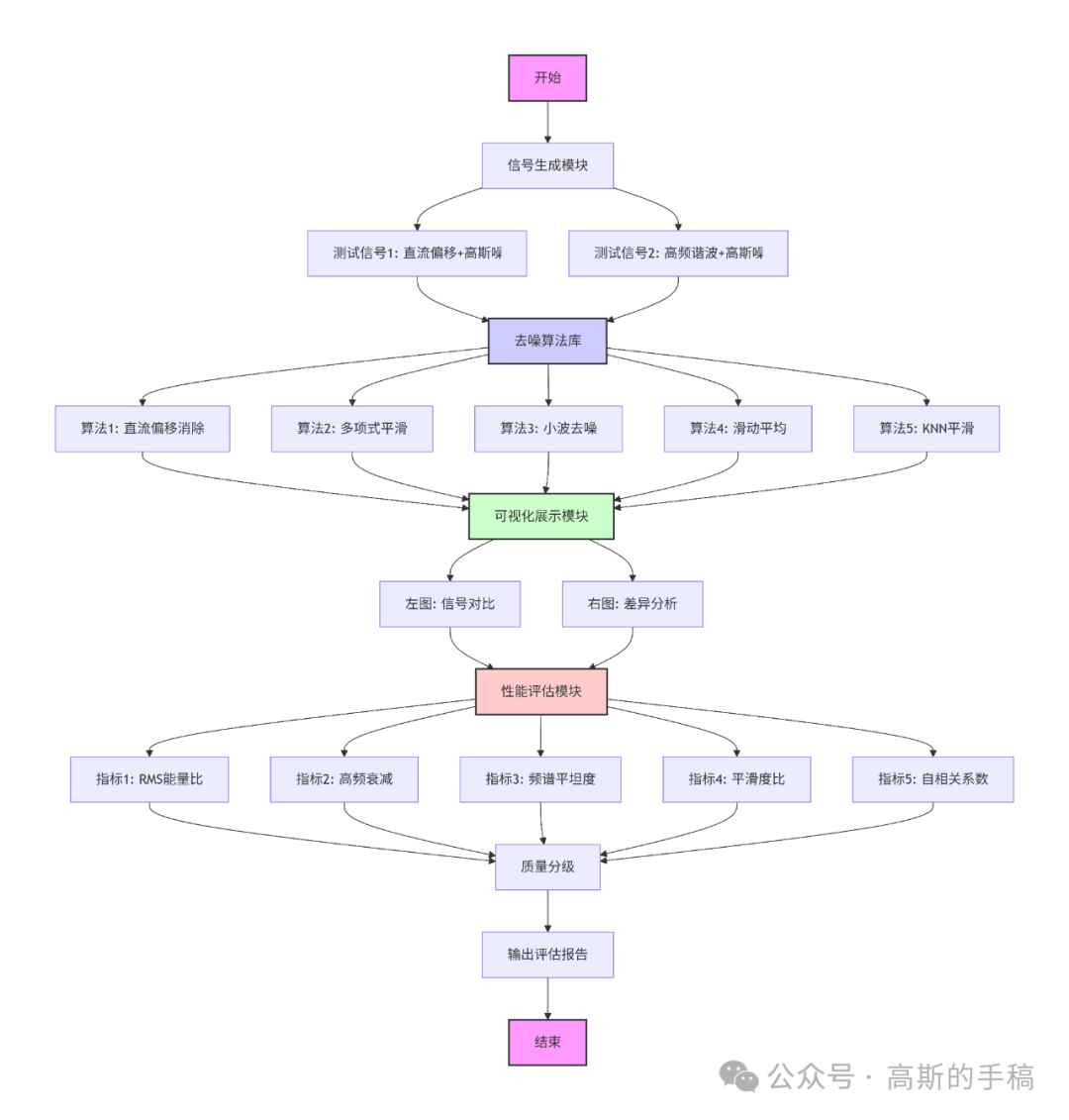
在信号处理实践中，为了全面评估不同算法的性能，我们首先构建了两种典型的测试信号。

• 第一种测试信号：包含显著直流偏移和高斯噪声的简单正弦波，主要用于测试直流分量去除算法的效果。
• 第二种测试信号：包含高频谐波和高斯噪声的复合信号，用于评估高频噪声抑制和信号平滑算法的能力。

我们集成了五种不同的去噪算法，每种算法都针对特定的噪声特性设计：

1. 基线校正 (Baseline Correction)：专门用于消除信号中的直流漂移或缓慢变化的基线。
2. 萨维茨基-戈莱平滑 (Savitzky-Golay Filter)：基于局部多项式拟合，能在平滑噪声的同时较好地保留信号的原始特征。
3. 小波软阈值去噪 (Wavelet Soft-Thresholding)：利用多尺度分析，有效分离噪声与有用信号成分。
4. 滑动窗口平均滤波 (Rolling Average Filter)：一种简单高效的低通滤波方法。
5. 自适应K近邻平滑 (Adaptive K-Nearest Neighbors Smoothing)：基于信号局部相似性进行自适应的平滑处理。

对于每种算法，系统通过可视化模块直观展示原始信号与处理后的信号的对比图，以及两者的差异图。更重要的是，系统内置了全面的量化评估模块。它通过计算五个关键指标——总体能量衰减比、高频噪声功率衰减、频谱平坦度变化、时域平滑度比和一阶自相关系数变化，并结合预设的阈值标准给出质量分级评估（✅良好/⚠️警告/❌不良）。这种从多维度进行信号处理与性能分析的评估方式，最终以专业报告格式输出，为不同应用场景下选择最优去噪算法提供了科学的决策依据。

核心算法代码实现与解析

以下是部分核心算法的代码实现，结合了数据分析中常用的库和信号处理技术。

1. 可视化与评估函数

import pywt
from scipy.signal import savgol_filter, welch
import matplotlib.pyplot as plt

def plot_signal_comparison(data, modified_data, sample_index):
    """
    绘制原始信号与处理后信号的对比图
    """
    difference = np.array(data[sample_index]) - np.array(modified_data[sample_index])
    fig, axes = plt.subplots(1, 2, figsize=(14, 3))
    axes[0].plot(data[sample_index], color='blue', alpha=0.7, linewidth=1, label='Raw Signal')
    axes[0].plot(modified_data[sample_index], color='red', alpha=0.8, linewidth=1.5, label='Modified Signal')
    axes[0].set_xlabel('Time (samples)'); axes[0].set_ylabel('Amplitude'); axes[0].set_title('Raw vs Modified Signals')
    axes[0].legend(); axes[0].grid(True, alpha=0.3)
    axes[1].plot(difference, color='green', linewidth=1, label='Difference')
    axes[1].set_xlabel('Time (samples)'); axes[1].set_ylabel('Amplitude Difference'); axes[1].set_title('Difference Between Signals')
    axes[1].grid(True, alpha=0.3); axes[1].legend(loc='upper right')
    plt.tight_layout(); plt.show()

def evaluate_denoising_single(noisy_signal, filtered_signal, fs, method_name="Filtered Signal"):
    """
    综合评估去噪算法性能，输出五维指标报告。
    """
    # 计算RMS能量衰减比
    rms_noisy = np.sqrt(np.mean(noisy_signal**2))
    rms_filtered = np.sqrt(np.mean(filtered_signal**2))
    rms_ratio = rms_filtered / rms_noisy
    # 计算高频功率衰减（>50Hz）
    f, Pxx_noisy = welch(noisy_signal, fs=fs, nperseg=1024)
    _, Pxx_filtered = welch(filtered_signal, fs=fs, nperseg=1024)
    hf_band = f > 50
    hf_reduction_db = 10 * np.log10(np.sum(Pxx_filtered[hf_band]) / np.sum(Pxx_noisy[hf_band] + 1e-12))
    # 计算频谱平坦度
    def spectral_flatness(Pxx):
        geometric_mean = np.exp(np.mean(np.log(Pxx + 1e-12)))
        arithmetic_mean = np.mean(Pxx)
        return geometric_mean / (arithmetic_mean + 1e-12)
    sf_filtered = spectral_flatness(Pxx_filtered)
    # 计算平滑度比
    smoothness_ratio = np.mean(np.abs(np.diff(filtered_signal))) / (np.mean(np.abs(np.diff(noisy_signal))) + 1e-12)
    # 计算一阶自相关系数
    def normalized_autocorr(sig):
        sig = sig - np.mean(sig)
        ac = np.correlate(sig, sig, mode='full')
        ac = ac[ac.size // 2:]
        return ac[1] / ac[0] if ac[0] != 0 else 0
    ac_filtered = normalized_autocorr(filtered_signal)
    # 质量分级评估逻辑（示例：RMS指标）
    def quality_flag(metric_name, value):
        if metric_name == "RMS":
            if value < 0.6: return "⚠️ Over-attenuated"
            elif value < 1.0: return "✅ Reasonable"
            else: return "❌ Possibly under-filtered"
        # ... 其他指标（HF, SF, SMOOTH, AC）的评估逻辑类似
    # 打印评估报告
    print(f"\n=== Noise Removal Quality Evaluation: {method_name} ===")
    print(f"{'Metric':35s} {'Value':>10s} {'Assessment':>25s}")
    print("-" * 80)
    print(f"{'RMS Reduction Ratio':35s} {rms_ratio:10.3f} {quality_flag('RMS', rms_ratio):>25s}")
    print(f"{'High-Freq Power Reduction (dB)':35s} {hf_reduction_db:10.2f} {quality_flag('HF', hf_reduction_db):>25s}")
    # ... 打印其他指标
    print("-" * 80)

2. 测试信号生成

def generate_noisy_signal_1():
    """生成含直流偏移和高斯噪声的正弦波信号。"""
    fs = 1000
    t = np.linspace(0, 2, 2 * fs)
    clean_signal = np.sin(2 * np.pi * 5 * t)
    noisy_signal = clean_signal + 1.5 + 0.1 * np.random.randn(len(t)) # 直流偏移1.5，高斯噪声
    return clean_signal, [noisy_signal], fs

def generate_noisy_signal_2():
    """生成含高频谐波和高斯噪声的复合信号。"""
    fs = 1000
    t = np.linspace(0, 2, 2 * fs)
    clean_signal = np.sin(2 * np.pi * 5 * t) + 0.3 * np.sin(2 * np.pi * 20 * t)
    noisy_signal = clean_signal + 0.5 * np.random.randn(len(t))
    return clean_signal, [noisy_signal], fs

3. 五大去噪算法实现

def simple_mean_subtraction(signal, fs, baseline_duration):
    """基线校正：去除直流偏移。"""
    signal_list = []
    baseline_samples = int(baseline_duration * fs)
    for sig in signal:
        baseline = sig[:baseline_samples]
        cleaned_signal = sig - np.mean(baseline)
        signal_list.append(cleaned_signal)
    return np.array(signal_list)

def savgol_smoothing(signal, window_length, polyorder):
    """萨维茨基-戈莱平滑滤波。"""
    smooth_list = []
    for sig in signal:
        smoothed = savgol_filter(sig, window_length, polyorder)
        smooth_list.append(smoothed)
    return np.array(smooth_list)

def wavelet_denoising(signal, wavelet='db4', level=3):
    """小波软阈值去噪。"""
    denoised_list = []
    for sig in signal:
        coeffs = pywt.wavedec(sig, wavelet, level=level)
        sigma = np.median(np.abs(coeffs[-1])) / 0.6745
        uthresh = sigma * np.sqrt(2 * np.log(len(sig)))
        coeffs[1:] = [pywt.threshold(c, value=uthresh, mode='soft') for c in coeffs[1:]]
        denoised = pywt.waverec(coeffs, wavelet)
        denoised_list.append(denoised[:len(sig)])
    return np.array(denoised_list)

def rolling_average(signal, window_size=51):
    """滑动窗口平均滤波。"""
    smoothed_list = []
    for sig in signal:
        smoothed = np.convolve(sig, np.ones(window_size)/window_size, mode='same')
        smoothed_list.append(smoothed)
    return np.array(smoothed_list)

def knn_filter(signal, k=5, search_radius=50):
    """自适应K近邻平滑。"""
    filtered_list = []
    for sig in signal:
        N = len(sig)
        filtered = np.zeros(N)
        for i in range(N):
            start, end = max(0, i-search_radius), min(N, i+search_radius)
            neighbors = sig[start:end]
            distances = np.abs(neighbors - sig[i])
            k_indices = np.argsort(distances)[:k]
            filtered[i] = np.mean(neighbors[k_indices])
        filtered_list.append(filtered)
    return np.array(filtered_list)

算法效果可视化对比

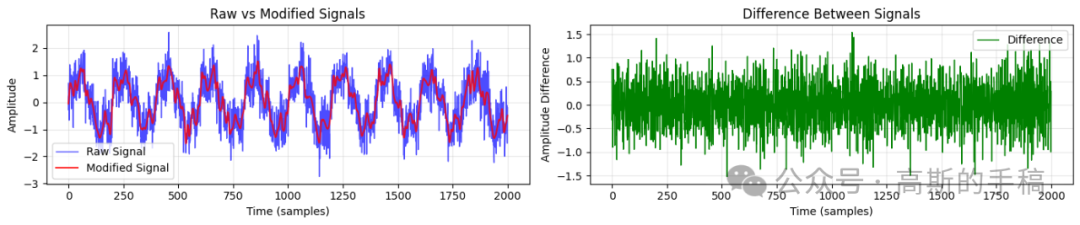
通过调用上述函数，我们可以对每种算法进行测试，并直观地比较其去噪效果。下图展示了萨维茨基-戈莱平滑算法处理含高频谐波信号前后的对比及差异。

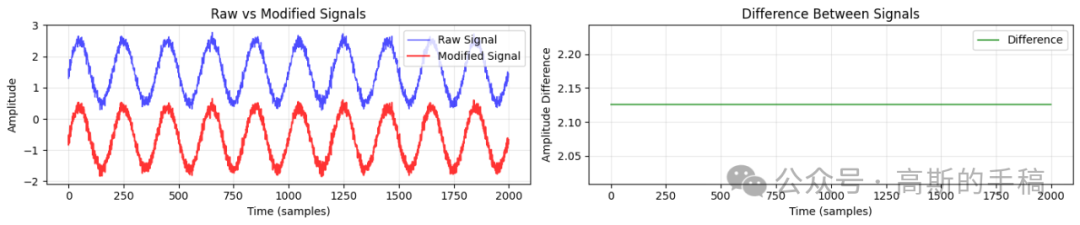
小波去噪算法在处理同类信号时，展现了其多尺度分析的强大能力，能有效剥离噪声同时保留信号边缘。

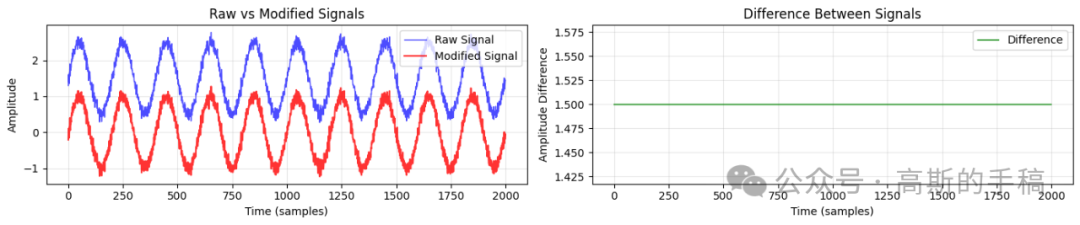
对于简单的滑动平均滤波，其平滑效果明显，但可能导致信号细节丢失。

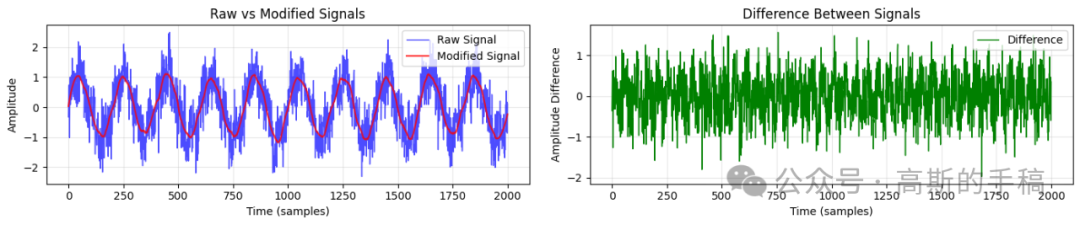
自适应KNN平滑算法根据信号局部结构进行调整，在平滑噪声和保持细节之间取得了不错的平衡，这种基于相似性度量的思路也与一些机器学习方法有相通之处。

最后，基线校正算法专门针对第一种含直流偏移的信号。下图展示了使用不同基线时长（0.1秒 vs 2秒）进行校正的结果对比。可以看到，使用整个信号时长（2秒）作为基线能更准确地移除直流分量。

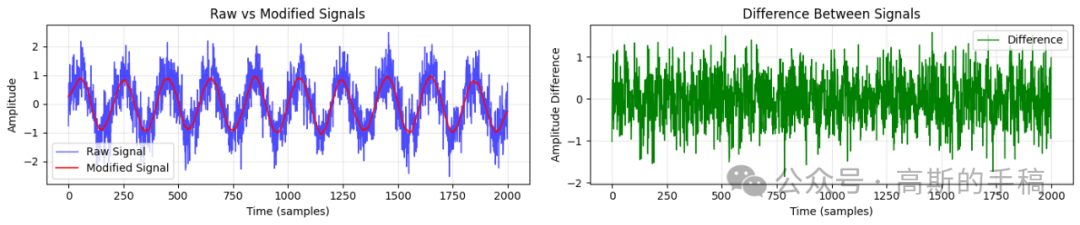
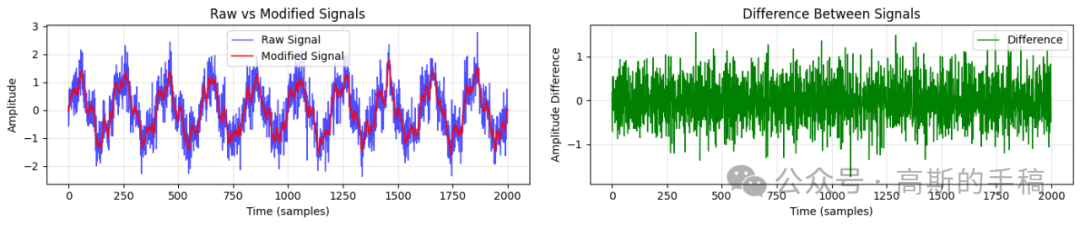
通过上述完整的代码实现、可视化对比和量化评估，我们系统性地展示了从基础校正到智能平滑的多种时域信号净化技术，为工程实践中的算法选型提供了清晰的参考。