基于Transformer的FinPFN元学习框架在股票收益率预测中的应用与机制转换适应

股票收益率预测是实证资产定价领域的核心难题。研究表明，预期收益率及其可预测性并非恒定，而是会随着市场机制、经济状态的改变而波动。预测因子（无论是公司特征、宏观变量还是技术指标）与收益率之间的关系是动态演化的。这一特性对传统计量经济学模型和常规机器学习方法构成了严峻挑战，因为它们通常假设从特征到收益的映射关系是稳定的。忽视这种结构性不稳定，会导致模型在样本外预测时性能显著下降。

尽管机器学习在捕捉非线性与交互效应方面展现出强大能力，并因此在资产定价中受到重视，但多数模型依赖于混合样本估计，并假设数据生成过程平稳。当市场发生机制转换或概念漂移时，这一假设便不再成立，因为预测因子的信息相关性是状态依赖且时变的。

为应对这一挑战，本文提出了一种专为提升机制转换环境下横截面收益预测能力而设计的元学习框架。其核心洞见在于：预测信号的有效性随市场状态和宏观经济条件而变化。因此，我们不学习一个固定的特征-收益映射，而是将收益预测重构为一个序列到序列的任务，让模型学习市场状态如何随时间演变。通过以最近观察到的特征-收益关系为条件来生成预测，模型能够自然地适应结构性变化与信息相关性的动态演化，而无需显式的机制标签或频繁的重新训练。

本文使用基于Transformer的贝叶斯预测器——金融先验数据拟合网络（Financial Prior-data Fitted Network, FinPFN）来实现该框架。与在合成数据上训练的原始PFN不同，FinPFN直接在真实金融时序数据上进行元训练，从而构建了专为资产收益率机制转换特性定制的金融先验。实证结果表明，FinPFN在中国A股市场（日频）和美国股市（月频）上均显著优于传统基准模型，尤其在波动率剧烈变化的机制转换时期，其优势更为突出。

背景

资产定价中的时变预期收益与机制转换

实证资产定价的一个核心观点是，预期收益率会随着宏观经济条件、投资者偏好和市场结构的变化而波动。经典的马尔可夫机制转换模型被广泛用于捕捉牛熊市转换、波动率状态和风险溢价的变化。研究表明，忽略这种机制动态性会导致显著的预测误差和投资损失，尤其在市场动荡时期。

预测指标与收益率之间的关系在时间上也是不稳定的。例如，在经济衰退期，收益率的可预测性往往更强。这种不稳定性严重限制了基于混合历史数据或静态参数假设训练的模型，因为它们无法捕捉预测因子信息相关性的状态依赖性变化。

本文将收益预测重构为定义在连续时期上的一个元任务序列。模型通过以最近观察到的特征-收益关系作为先验条件，学习近期的横截面行为如何为下一期收益提供信息，从而使预测映射能够灵活适应变化的市场环境。

元学习与Prior-data Fitted Networks (PFN)

常规监督学习旨在优化模型参数，使其预测逼近训练目标，并在独立的测试集上评估性能。这要求特征与目标之间的关系在训练和测试阶段保持稳定，而市场机制转换往往违背了这一平稳性假设。

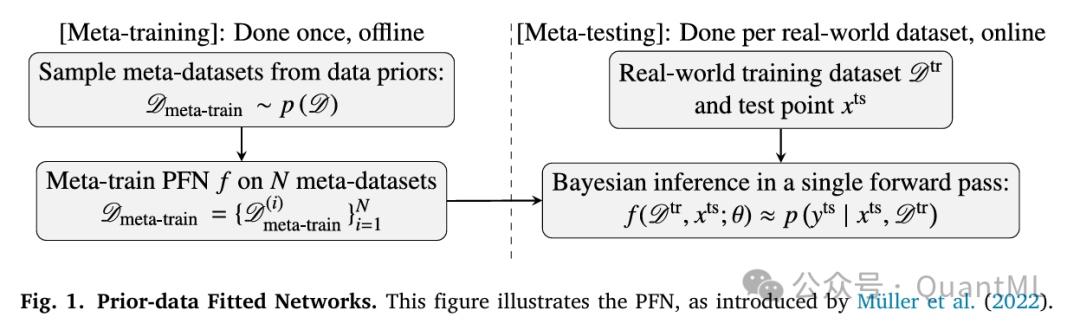
元学习的目标是“学会学习”。在元学习框架下，模型将训练数据和测试特征同时作为输入，通过元训练优化其参数，使其能够直接将新的数据集映射到预测目标。一旦预训练完成，元模型仅需一次前向传播即可对新数据进行预测，无需重新估计参数。

先验数据拟合网络（PFN）是一种利用深度学习进行贝叶斯推断的元学习方法。PFN将监督学习问题视为贝叶斯推断，即在给定训练集的情况下计算测试目标的后验预测分布。通过训练一个带有Softmax输出的深度学习模型来近似这个概率分布，PFN最小化了模型预测与真实后验分布之间的Kullback-Leibler散度。

传统的PFN通常在合成数据集上进行元训练，以解决元任务数据稀缺的问题。TabPFN是PFN的一个扩展，它通过在结构因果模型生成的合成表格数据上训练，专注于解决通用表格数据的分类与回归问题。

数据与方法论

数据描述与问题构建

本文在两个大规模的股票数据集上评估FinPFN，这两个数据集在市场结构和时间频率上存在显著差异。

1. 中国股市数据（CSI 500）：
   • 资产： 中证500指数成分股，涵盖500只中盘A股。
   • 频率： 日频预测。
   • 时间跨度： 2016年1月至2023年4月，包含超过100万个股票-日观测值。
   • 特征： 30个特征，主要为价格相关的技术指标和高频指标。
   • 目标： 经过Barra风险模型调整后的收益率，以控制规模、价值、动量等系统性风险因子。
   • 划分： 元训练期（2016-2021），验证期（2021-2022），样本外测试期（2022-2023）。
2. 美国股市数据：
   • 资产： 约30,000只公开上市的美股，数据源自Gu et al. (2020)的经典研究。
   • 频率： 月频预测。
   • 时间跨度： 1962年至2021年。
   • 特征： 90个特征，包含技术指标以及季度/年度基本面变量。
   • 目标： 未来1个月的收益率。
   • 划分： 元训练期（1962-1999），验证期（2000-2009），样本外测试期（2010-2021）。

对于两个数据集，所有特征均在每个时间点的横截面上进行标准化和去极值处理，缺失值使用横截面中位数填充。

评估指标：信息比率

鉴于横截面资产选择的核心目标是对股票的相对表现进行排序，而非预测精确的收益率水平，本文采用信息比率作为主要的评估指标。

首先，计算每个时间点的信息系数，它定义为预测收益率与实际收益率之间的横截面斯皮尔曼秩相关系数。

随后，信息比率计算为整个测试期内IC序列的均值除以其标准差：

[ IR = \frac{\text{Mean}(IC_t)}{\text{Std}(IC_t)} ]

更高的IR表示预测能力更强且更稳定。为评估统计显著性，本文通过对样本外测试期进行重复子采样来构建置信区间。

基准模型

为了进行全面对比分析，本文选取了以下几类基准模型：

• 朴素基准：
  • “Prev”：使用股票上一期的收益率作为当前期的预测值，用于捕捉短期动量或反转效应。
  • “Prev Year”：使用过去12个月的平均收益率作为预测值。
• 线性模型：
  • Ridge回归： 施加L2惩罚项的线性回归，用于处理特征间的多重共线性和过拟合问题。
• 树模型：
  • 随机森林： 鲁棒的集成模型，通常在金融噪声数据中表现稳健。
  • LightGBM： 高性能的梯度提升树框架，在表格数据预测中表现出色。
• 神经网络：
  • 多层感知机： 具有非线性激活函数的前馈神经网络。
• 元学习基准：
  • TabPFN： 未经修改的原始TabPFN模型，用于对比并凸显FinPFN采用金融领域先验训练的增量价值。

PFN中的Transformer架构

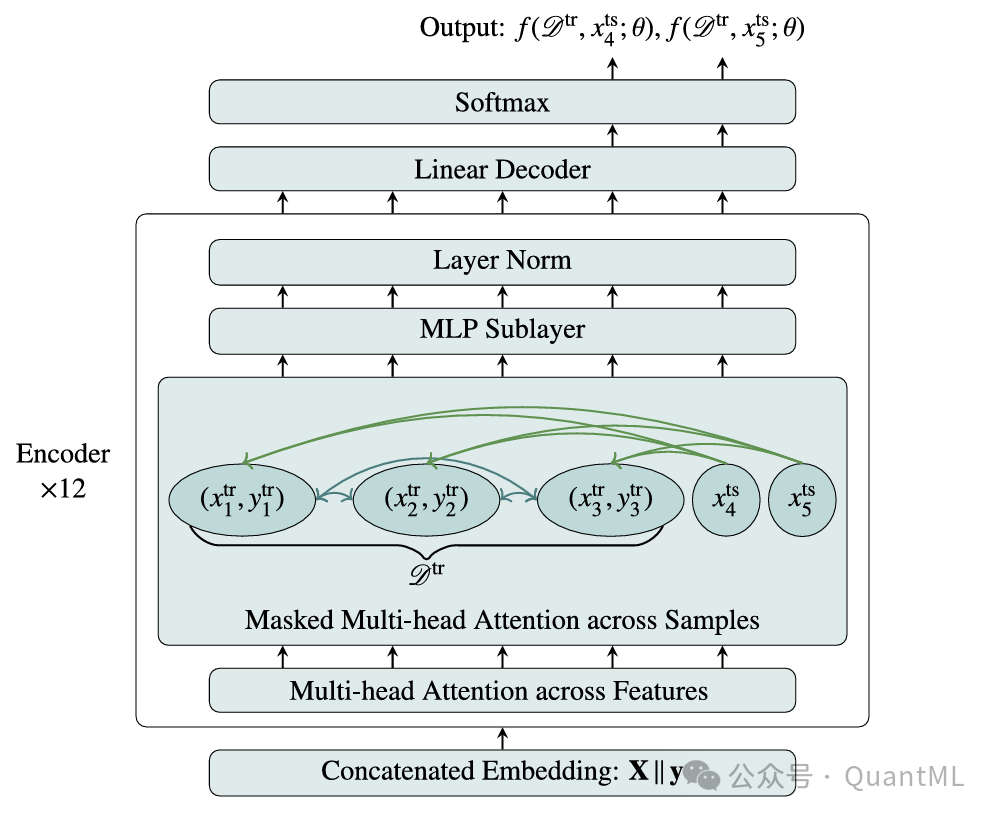
本文的FinPFN建立在Hollmann等人提出的TabPFN架构之上。该架构使用Transformer编码器来处理两个可变长度的集合：训练集和测试集。

• 输入处理： 每个样本（股票）被视作一个Token。训练Token嵌入了其特征值和目标值，而测试Token仅嵌入其特征值。使用位置编码来区分特征列和目标列。
• 注意力机制： 编码器包含12层，交替使用两种注意力块：
  • 特征间注意力： 列式操作，捕捉单只股票内部不同特征之间的上下文关系。
  • 样本间注意力： 行式操作，学习不同股票之间的关系。
• 掩码机制： 采用因果掩码方案，防止测试Token关注其他测试Token，确保严格的因果关系，避免信息泄露。训练Token可以相互关注，而测试Token只能关注训练Token。
• 输出： 编码器的输出通过一个线性解码器生成每只股票预测分布的直方图，最终的点预测取该分布的中位数。

Financial Prior-data Fitted Network (FinPFN)

FinPFN的核心创新在于利用真实金融时序数据构建元学习任务，而非使用合成数据。

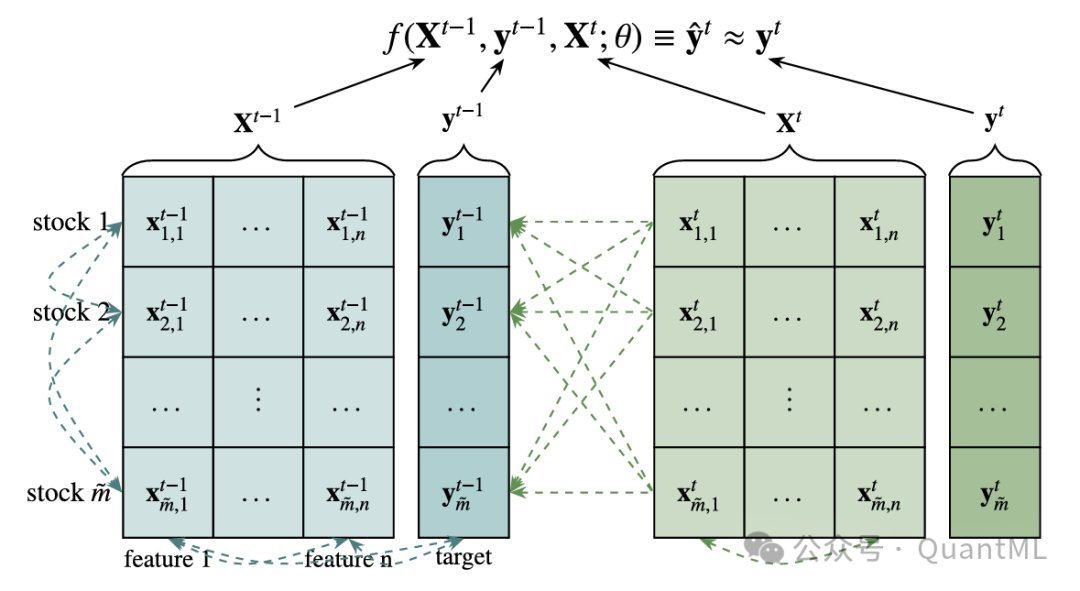
1. 任务重构：本文将收益预测重构为相邻时间段的一系列元任务。在每个时间步t，定义元数据集 ( Dt = {(X{t-1}, r_{t-1}), X_t} )，其中目标是 ( rt )。模型利用历史数据作为“上下文”，即上一期的特征和收益 ( (X{t-1}, r_{t-1}) )，来预测当前期的收益 ( r_t )。这种结构不假设特征到收益的映射在所有时间都是固定的，而是假设“从t-1期到t期”的关系是从一个稳定的元分布中采样的。

2. 注意力机制的应用：如图3所示，自注意力机制允许时间t-1的所有股票特征和目标相互关注。时间t的股票特征关注其自身在t-1期的特征和目标，但受限于因果掩码，不能获取未来的信息。

3. 计算效率与采样：由于自注意力机制的计算复杂度随股票数量N的平方增长（O(N²)），直接处理所有股票（如500只）成本过高。FinPFN采用随机子采样策略：

• 在训练和推断时，随机抽取N只股票（N<总股票数）作为一个组。
• 对于全市场预测，将股票随机划分为多个组（例如10组，每组50只），分别进行预测。
• 组内的收益率进行横截面标准化（均值为0，标准差为1），称为相对收益。

4. 训练过程：

• 数据先验： 区别于TabPFN使用合成结构因果模型，FinPFN直接在真实历史金融数据上进行元训练，以学习符合资产收益率统计特性（如尖峰厚尾、时变波动率、低信噪比）的先验分布。
• 参数设置： 批量大小为64（随机采样的日期），每个日期随机选取50只股票。训练使用Adam优化器，学习率为 ( 10^{-4} )。
• 推断： 一旦元训练完成，FinPFN可以在单次前向传播中对新数据进行预测，无需重新训练或微调，这极大地提高了在实时大数据应用中的效率。

预测结果

预测性能评估

在样本外测试期（CSI 500: 2022-2023; 美股: 2010-2021），FinPFN展现了卓越的预测能力。

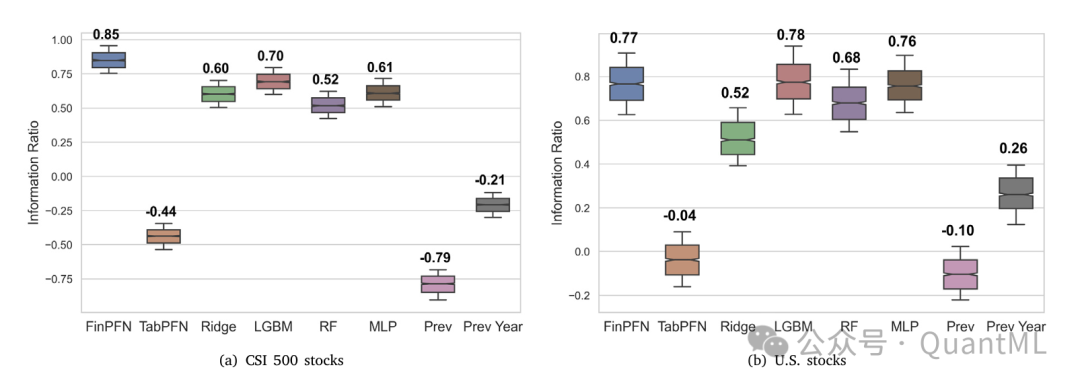
• 整体表现： 如图4所示，FinPFN在两个市场中均显著超越了朴素基准。
  • CSI 500： FinPFN的信息比率高达0.85，远高于“Prev” (-0.79) 和 “Prev Year” (-0.21)。“Prev”的极低表现反映了中国A股市场日频数据强烈的反转特征。
  • 美国股市： FinPFN的信息比率为0.77，同样优于朴素基准。
• 对比TabPFN： 原始TabPFN表现糟糕（CSI 500: -0.44; 美股: -0.04），且其预测结果与“Prev”策略高度相关。这表明通用表格模型主要是在记忆最近一期的结果，未能学习到有意义的时序动态，凸显了使用特定领域金融数据进行训练的必要性。
• 对比树模型： FinPFN的表现也超越了主流树模型。在CSI 500上，FinPFN (0.85) 显著优于LightGBM (0.70) 和随机森林 (0.52)。在美股市场上，FinPFN (0.77) 与表现最佳的LightGBM (0.78) 相当，优于随机森林 (0.68)。

投资组合表现

为了评估预测排名的经济价值，本文构建了十分位投资组合，并重点关注多空组合的表现。

• CSI 500： 如表2所示，基于FinPFN预测构建的多空组合实现了9.8的年化夏普比率（未计交易成本），显著高于第二名LightGBM的7.3。这一优势主要源于FinPFN识别最高十分位（预期收益最高）股票的卓越能力。值得注意的是，预测中最低十分位（理论应做空）的股票在中国市场有时实际收益较高，这与卖空限制、T+1交易规则等市场摩擦有关。
• 美国股市： FinPFN构建的多空组合夏普比率为2.1，与LightGBM（2.2）表现相当。

机制转换期间的预测性能

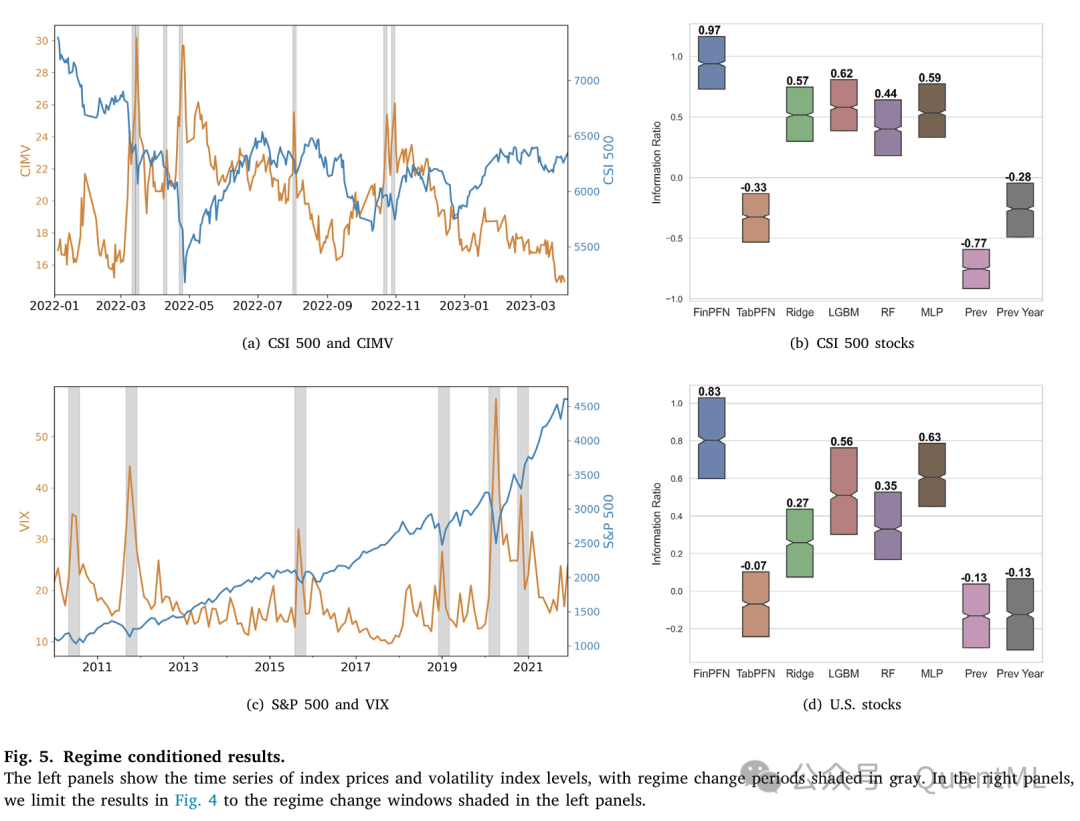
本文的核心动机是解决市场机制变化下的预测难题。机制转换被定义为市场波动率指数（中国使用CIMV，美国使用VIX）的急剧上升并持续处于高位。

• 机制识别：
  • 中国市场：CIMV单日上升超过2.5点且水平超过20。
  • 美国市场：VIX单月上升超过10点且水平超过30。
• 结果分析： 如图5所示，在机制转换发生后的评估窗口内，传统基准模型（特别是随机森林和梯度提升树）的性能显著恶化。这些模型依赖于假设关系稳定的历史模式，因此在收益生成过程快速变化的环境中表现不佳。
• FinPFN的鲁棒性： 相比之下，FinPFN在动荡时期保持了高预测精度，并始终优于所有其他模型。
  • 在CSI 500数据上，FinPFN在机制转换期间的信息比率高达0.97，比次优模型（0.62）高出50%以上。
  • 在美国数据上，FinPFN的信息比率为0.83，比第二名（0.63）高出30%以上。

这一结果有力地支持了本文的假设：通过训练模型将最近期的市场结果与当前收益联系起来，FinPFN比基于静态或混合历史数据训练的模型更能有效地适应新环境。

鲁棒性分析

为了验证结果的可靠性，本文进行了一系列鲁棒性检验：

1. 特征构建时点： 确认了所有特征计算仅使用t期及之前的信息，彻底消除了前视偏差，确保预测在实盘交易中是可行的。
2. 预测目标期限： 将预测目标扩展为t到t+5期的平均收益。FinPFN依然保持优越性能，表明其预测不仅仅是捕捉暂时的价格压力或流动性效应。
3. 机制阈值敏感性： 对定义机制转换的波动率水平、变化幅度和评估窗口长度进行了多组测试。在所有替代设定下，FinPFN在动荡时期的表现优势均保持不变。且随着评估窗口缩短，FinPFN的相对优势增加，表明其特别擅长捕捉机制转换后的即时动态。
4. 回看滞后期： 测试了使用t-2期或t-3期代替t-1期作为条件输入。结果显示性能随滞后期增加而稳步下降（IR从0.85降至0.53和0.45）。这符合预期，即更久远的数据包含的时效性信息较少，但同时也验证了“基于最近期状态进行条件预测”这一元水平稳定性假设的有效性。

结论

本文针对资产收益可预测性的状态依赖性特征，提出了一种名为FinPFN的新型元学习框架。该框架摒弃了特征到收益映射稳定的传统假设，转而学习从近期市场条件到未来收益的动态映射，以最近观察到的特征-收益关系为条件进行预测。具体而言，FinPFN以情景式方式运行，根据上一时间步的横截面数据元学习预测当前横截面的收益。

实证结果表明，FinPFN在中国和美国两个截然不同的股票市场中，均一致地优于广泛的基准模型。虽然其平均性能在某些时期与最佳基准相当，但在波动率加剧的机制转换时期，FinPFN表现出极高的有效性与鲁棒性。在这些关键时期，预训练好的FinPFN能够通过单次前向传播提供快速推断，支持快速自适应的投资决策与组合调整。

本文提出的方法具有良好的扩展性。未来的研究可以探索将多个前期时段作为条件输入，或者设计跨时间、资产和特征的三维注意力机制，以捕捉更高阶的跨机制依赖关系。虽然这种扩展会增加计算复杂度，但可以通过Linformers或Performers等高效注意力变体来解决。

此外，本文的工作也引发了关于如何将FinPFN等数据驱动的机器学习模型与正式的资产定价理论相结合的思考。传统方法通过条件因子模型来估计时变风险溢价，而FinPFN是模型无关且完全由数据驱动的。未来的一个重要方向是弥合这一差距，探索将元学习方法嵌入结构化理论模型中，或设计一种能结合理论约束与学习型自适应能力的混合框架。