Python/PyTorch实战：基于注意力机制的端到端量化投资组合优化

1. 引言：从“预测-优化”分离到端到端学习

在传统的量化投资组合管理中，现代投资组合理论（MPT）通常遵循一个两步走的范式：

1. 参数估计：预测资产收益率向量 $\mu$ 和协方差矩阵 $\Sigma$。
2. 均值-方差优化：将上述估计值代入优化器求解最优权重。

然而，这种分离的方法面临着著名的“误差最大化”问题：优化器倾向于赋予那些估计误差最大的资产过高的权重。此外，协方差矩阵的估计在资产数量增加时极其不稳定。

本文将介绍一种端到端的深度学习框架。它不显式预测收益或波动，而是直接将资产特征映射为投资组合权重。这种方法基于 Brandt, Santa-Clara, and Valkanov (2009) 的参数化投资组合策略（Parametric Portfolio Policies），并巧妙结合了现代注意力机制，以捕捉时间序列的长记忆特征和非线性关系。

2. 数学模型构建

2.1 问题定义

假设我们需要在 $N$ 个资产中进行配置。定义 $r_{i,t}$ 为资产 $i$ 在 $t-1$ 到 $t$ 期间的收益率。定义 $f_{i,t}$ 为资产 $i$ 在 $t$ 时刻可观测到的特征向量。

我们的目标是寻找一个映射函数 $g$，它根据当前信息直接输出下一期的最优权重 $w_{t+1}$。

2.2 参数化权重函数

我们将投资组合权重 $w_{i, t+1}$ 参数化为特征 $f_{i, t}$ 的函数，由参数 $\theta$ 控制：

投资组合在 $t+1$ 时刻的收益率 $R_{p, t+1}$ 为：

2.3 优化目标

不同于最小化预测误差（如 MSE），我们的目标是最大化投资组合在整个样本周期 $T$ 内的某种效用函数 $U$ 的期望值。

定理 1 (端到端优化目标) 寻找最优参数 $\theta$ 等价于求解以下最大化问题：

证明与解释：该目标函数直接连接了输入特征 $f_{i,t}$ 和最终的投资效用 $U$。通过链式法则，梯度可以从效用函数直接回传至神经网络参数 $\theta$。这种方法绕过了对 $\mu$ 和 $\Sigma$ 的中间估计，使得模型能够专注于那些对最终组合表现有贡献的特征，而非仅仅是对单个资产收益预测准确的特征。

3. 损失函数与高阶矩偏好

框架的灵活性在于效用函数 $U$ 的选择。我们可以选择夏普比率，也可以选择包含高阶矩信息的效用函数。

3.1 夏普比率

最直观的目标是最大化样本内的夏普比率。此时损失函数定义为负的夏普比率：

3.2 CRRA 效用函数与高阶矩

为了捕捉投资者对偏度的正向偏好和对峰度及尾部风险的厌恶，我们引入常相对风险厌恶（CRRA）效用函数。

定义 CRRA 效用函数为：

其中 $\gamma$ 为风险厌恶系数。

定理 2 (CRRA 的高阶矩性质) 最大化 CRRA 效用函数等价于同时最大化奇数阶矩（如均值、偏度）并最小化偶数阶矩（如方差、峰度）。

证明：对 $U_{\gamma}(x)$ 在 $x=1$ 处进行泰勒展开（Taylor Expansion）：

计算各阶导数在 0 处的值：

1. 零阶项：$U_{\gamma}(1) = \frac{1}{1-\gamma}$
2. 一阶导数：$U_{\gamma}'(1) = 1$ （注：此处基于论文假设的标准化处理）
3. 二阶导数：$U_{\gamma}''(1) = -\gamma$
4. 三阶导数：$U_{\gamma}'''(1) = \gamma(\gamma+1)$ （在特定参数下为正）
5. 四阶导数：$U_{\gamma}^{(4)}(1) = -\gamma(\gamma+1)(\gamma+2)$

代入泰勒展开式：

推论：观察上述展开式符号：

• 一阶（均值）系数为正。
• 二阶（方差）系数为负（$-\gamma/2$）。
• 三阶（偏度）系数为正（当 $\gamma > 0$ 时）。
• 四阶（峰度）系数为负。

这证明了使用 CRRA Loss 不仅优化了均值-方差权衡，还内嵌了对正偏度和低峰度的偏好，且无需像 MVO 那样显式估计协方差矩阵。

4. 神经网络架构设计

为了实现上述映射 $g_\theta$，我们设计了一个包含注意力机制的深度神经网络。

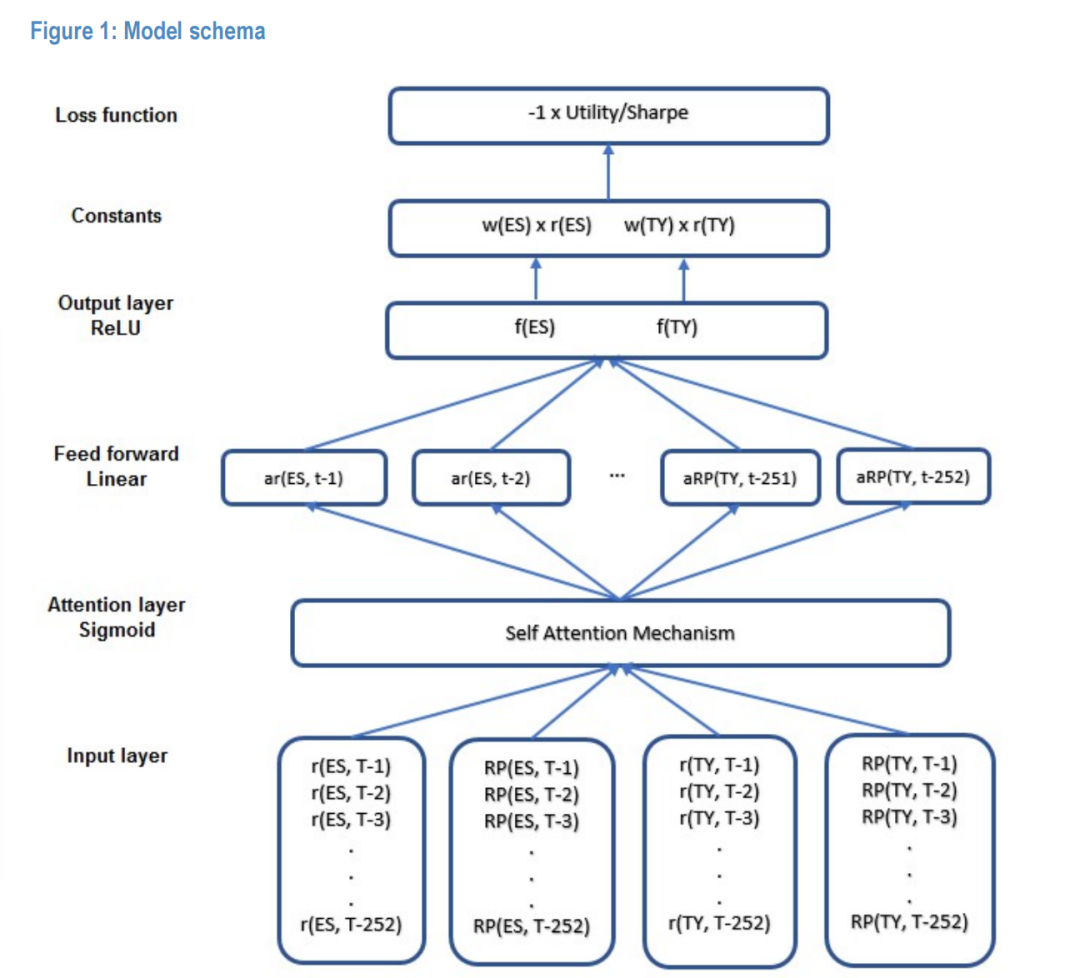
Figure 1：模型架构图，展示从输入层、注意力层、前馈线性层到输出层的完整流程。

4.1 输入层与特征处理

模型输入为过去 $L$ 天（例如 252 天）的资产特征序列。这确保了模型具有长期的记忆能力。输入张量维度为：$[B, N, L, F]$。

4.2 自注意力层 (Self-Attention Layer)

核心模块采用 Luong et al. (2015) 提出的乘法自注意力机制。注意力机制允许模型动态地赋予历史时间步不同的权重，识别出对当前时刻权重决策最重要的历史市场状态，从而捕捉时间序列中的非线性依赖。

激活函数采用 Sigmoid，以捕捉非线性特征。

4.3 权重收缩（Shrinkage）与基准锚定

为了提高策略的稳健性，防止过拟合，我们引入了向基准组合（如风险平价）收缩的机制。

定义 (基准锚定权重) 我们将最终输出的权重 $\tilde{w}_{i, t+1}$ 定义为神经网络原始输出 $m_{i, t+1}$ 与基准权重 $w_{i,t}^{benchmark}$ 的乘积：

其中：

• $w_{i,t}^{benchmark}$ 是预先确定的基准权重（例如基于最近 21 天波动率倒数的风险平价权重）。
• $m_{i, t+1}$ 是神经网络的输出，作为对基准权重的“乘数调整”（Multiplier）。

4.4 输出层激活函数

为了适应不同的投资约束，输出层激活函数 $\sigma$ 的选择至关重要：

• 纯多头限制 (Long-only)：使用 ReLU 函数，确保权重非负 ($\sigma(x) \ge 0$) 。
• 多空策略 (Long/Short)：可使用 Tanh 或 Linear 激活函数。
• 有界收缩：若使用 Sigmoid，则 $m \in (0, 1)$，这意味着策略权重严格向 0 收缩；若需要允许放大基准权重，ReLU 是更优选择。

在本框架的实证部分，我们主要关注多头策略，因此采用 ReLU 激活函数。

5. 实证分析设置

为了验证上述数学框架的有效性，我们在一个经典的股债配置（Bond/Equity Allocation） 问题上进行了实证检验。

5.1 数据与资产空间

• 资产选择：标普 500 指数期货（ES）代表权益类资产，10年期美国国债期货（TY）代表债券类资产。
• 数据频率：每日再平衡（Daily Rebalancing），目标是在周度（Weekly）视野下优化风险调整后收益。
• 输入特征：仅使用两类基础特征：
  1. 日度收益率 $r_{t}$。
  2. 已实现能量（Realized Power, $RP_t$）的对数值。

5.2 训练协议

• 滚动窗口：采用 2 年的滚动窗口进行训练，每月重新校准（Retrain）一次模型。
• 集成学习：为了消除随机种子的噪声影响，每个模型训练 10 次并取平均输出作为最终权重。
• 交易成本：假设双边交易成本均为 1bp。
• 基准：基于最近 21 天已实现波动率倒数的风险平价组合。

6. 结果与讨论：目标函数的实证影响

我们分别测试了两种不同的损失函数：CRRA 效用函数与夏普比率，以验证模型是否能通过端到端学习捕捉到特定的统计矩偏好。

6.1 场景 A：最大化 CRRA 效用（偏度偏好）

设定风险厌恶系数 $\gamma=5$。理论上，该设置应引导模型寻找正偏度的收益分布。

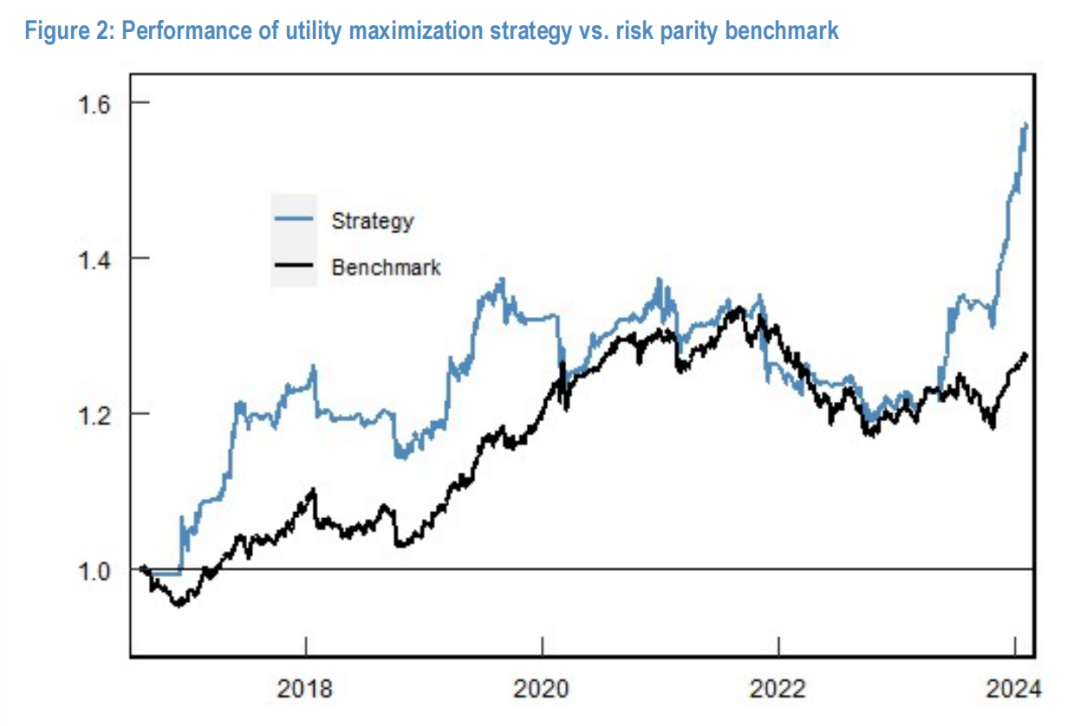
Figure 2：效用最大化策略（蓝线）与风险平价基准（黑线）的净值曲线对比。

实证结果：

1. 夏普比率提升：策略实现了 0.85 的夏普比率，显著高于基准的 0.63。
2. 偏度修正：最显著的差异在于偏度。基准组合呈现典型的负偏度（-0.78），而深度学习策略实现了正偏度（0.39）。

结论：模型成功内化了 CRRA 效用函数对高阶矩的偏好（即定理 2 中推导的对 $\mathbb{E}[(x-1)^3]$ 的正向系数），主动规避了尾部风险，从而实现了正偏度的收益分布。

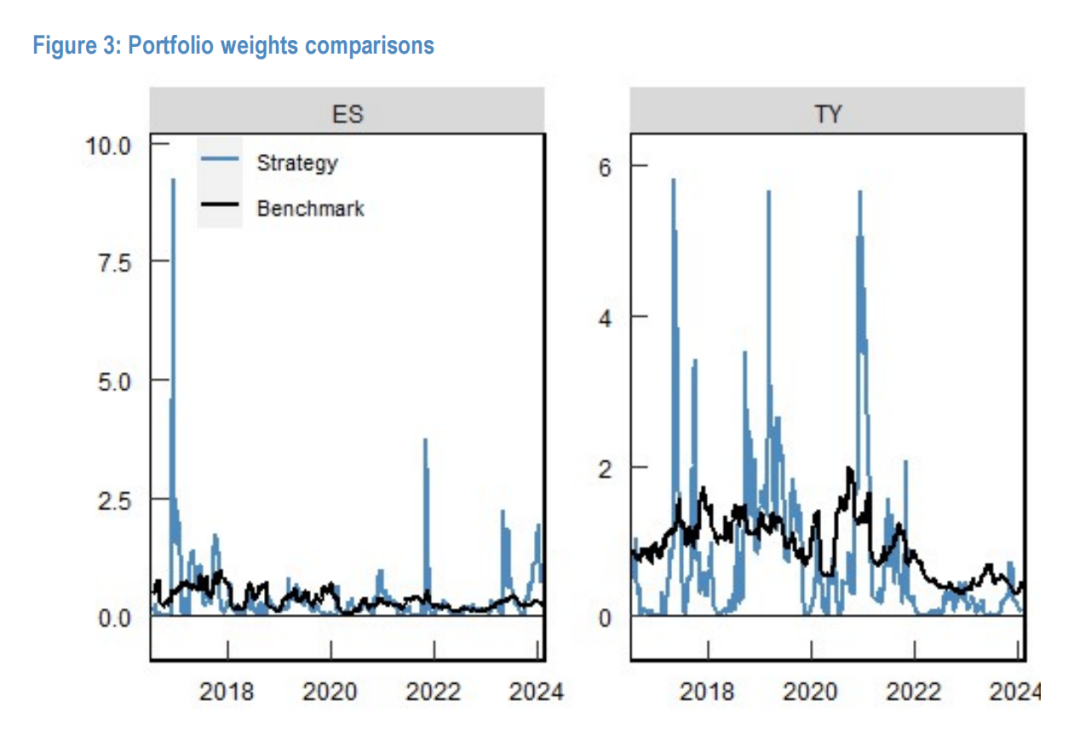
Figure 3：策略（蓝线）与基准（黑线）在ES（左）和TY（右）上的持仓权重动态变化。

6.2 场景 B：最大化夏普比率（均值-方差偏好）

在该场景下，损失函数仅关注一阶和二阶矩。

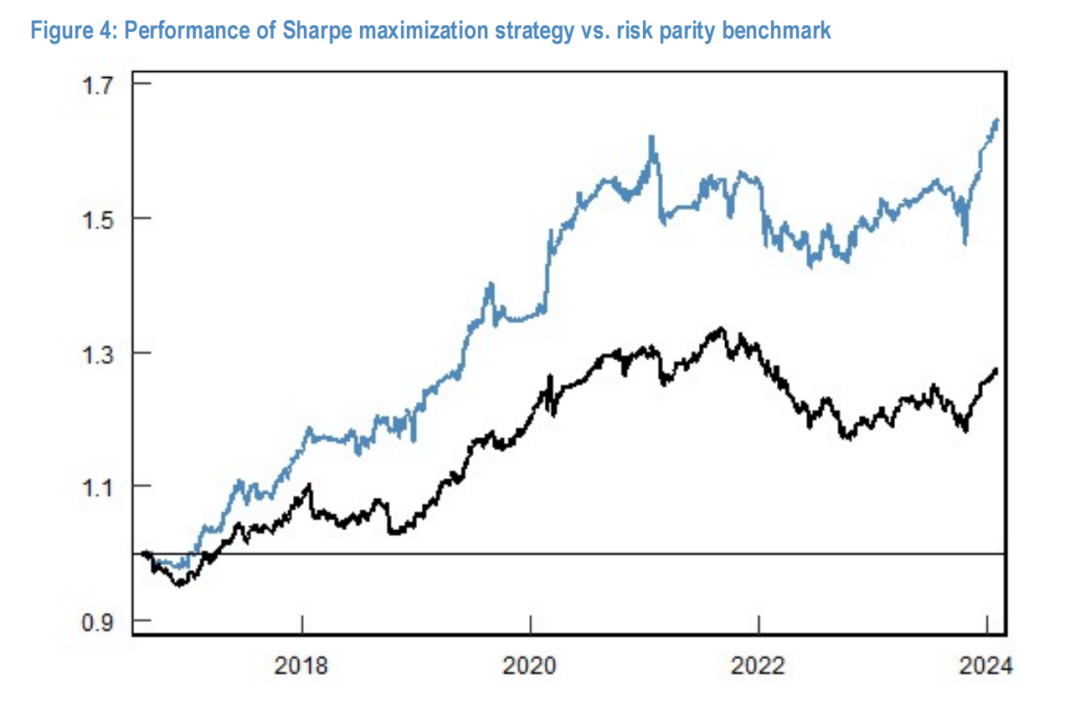
Figure 4：夏普最大化策略（蓝线）与基准（黑线）的净值曲线对比。

实证结果：

1. 夏普比率最大化：策略取得了 1.15 的夏普比率，优于 CRRA 效用场景（0.85）和基准（0.63）。
2. 偏度回归：偏度回落至 -0.63，与基准的 -0.78 类似。

结论：当剥离对高阶矩的偏好后，模型纯粹追求风险调整后收益的最大化，虽然牺牲了尾部保护（负偏度），但换取了更高的夏普比率。这证明了端到端框架能够精确执行预设的数学目标。

7. 特征工程的重要性：数据质量定理

在深度学习中，输入数据的信噪比至关重要。本节我们通过数学推导解释为何引入高频数据构建的特征能显著提升模型表现。

7.1 特征定义与对比

我们比较三种特征输入方案：

1. 方案 1：仅使用日度收益率 $r_t$。
2. 方案 2：日度收益率 + 日度绝对收益 $|r_t|$。
3. 方案 3：日度收益率 + 已实现能量 $RP_t$。

其中，已实现能量定义为日内 5 分钟高频收益绝对值之和：

其中 $M$ 为每日的 5 分钟区间数量（对于 24 小时交易的期货，$M \approx 288$）。

7.2 数据质量定理

定理 3 (高频采样降噪定理) 假设资产价格遵循几何布朗运动，且日内收益独立同分布（i.i.d.）。使用高频采样估计波动率特征的估计误差方差，与采样频率 $M$ 成反比。

证明：考虑估计日度波动率的代理变量。对于方案 2（日度绝对收益），我们仅有 1 个样本点，其标准误（Standard Error）为 $O(1)$。对于方案 3（已实现能量），我们利用了 $M$ 个观测值。根据大数定律（LLN）和中心极限定理（CLT），其标准误为 $O(\frac{1}{\sqrt{M}})$。

在本案例中，$M = 288$。因此，方案 2 包含的噪声大约是方案 3 的 $\sqrt{288} \approx 17$ 倍。

推论：深度学习模型对输入特征的噪声非常敏感。通过高频数据构建特征（方案 3），我们向模型提供了信噪比高出 17 倍的波动率信号，这将显著降低模型陷入局部最优的概率，并提高训练的稳定性。

7.3 实证验证

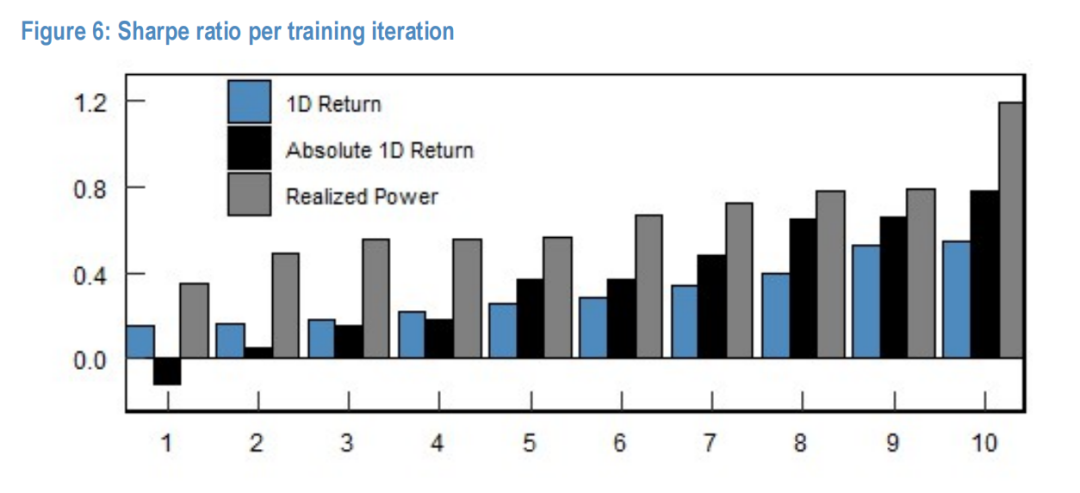
Figure 6：不同特征（1D Return， Absolute 1D Return， Realized Power）下模型在10次训练迭代中的平均夏普比率。

实验结果支持上述定理：

• 方案 1（纯日度）：平均夏普 0.31，标准差 0.14。
• 方案 3（高频特征）：平均夏普 0.67，标准差 0.23。

引入高频特征不仅通过经济学逻辑提供了更多信息，更通过统计学上的降噪效应，使模型能够更有效地学习市场规律。

8. 结论

本文构建了一个基于注意力机制的端到端深度学习投资组合优化框架。相比传统的“预测-优化”两步法，该框架具有以下核心优势：

1. 端到端目标导向：直接优化投资者关心的最终效用（如 CRRA 或 Sharpe），避免了中间变量（如协方差矩阵）估计误差的传导。
2. 高阶矩感知：通过灵活的损失函数设计（如 CRRA），模型能够内化对偏度、峰度等高阶统计特征的偏好，无需复杂的数学约束。
3. 非线性与长记忆：利用自注意力机制（Self-Attention），有效捕捉了长达 252 天的时间序列依赖和非线性特征。
4. 特征工程的数学基础：证明了基于高频数据的特征工程（Realized Power）能够通过降低估计方差，显著提升深度学习模型的收敛效果。

这一框架展示了深度学习在现代量化投资组合管理中的巨大潜力，即从单纯的“预测价格”转向“学习最优决策”。如果你对算法在金融工程中的具体实现感兴趣，可以访问 云栈社区 获取更多实战代码和讨论。