MinHash算法解析：高效解决海量文本相似度去重与Jaccard计算难题

在处理大模型训练数据清洗时，我遇到了一个棘手问题：如何从10亿条文本中快速找出相似重复项？

最初的思路很直接：使用Python的set()去重。但实际操作中遇到了两大障碍：

1. 内存直接溢出（将10亿个字符串同时加载到内存中是不现实的）。
2. 需求并非精确匹配，而是需要找出“近似相似”的文本（例如，仅修改了少量标点符号的两篇文章也应被视为重复）。

在团队讨论中，有同事提到了“MinHash”和“LSH”算法。经过一周的研究与实践，我终于理解了其原理。本文将梳理我的理解过程，希望能帮助遇到类似问题的开发者。

核心问题：如何定义“相似”？

理解MinHash前，需要先掌握Jaccard相似度的概念。它用于衡量两个集合的相似性。

假设有两篇文章，将其视为词集合：

A = {“我”, “喜欢”, “吃”, “苹果”}
B = {“我”, “喜欢”, “吃”, “香蕉”}

它们的Jaccard相似度计算公式为：

Jaccard(A, B) = len(A ∩ B) / len(A ∪ B)
               = 交集大小 / 并集大小
               = 3 / 5 = 0.6

值越接近1，表示两个集合越相似。

挑战在于：对于10亿条文本，两两计算Jaccard相似度的复杂度是O(n²)，计算量巨大，无法完成。

MinHash的价值：它将每个文本（集合）压缩成一个固定长度的“指纹”（签名数组），通过比较指纹即可快速估算出原始文本间的Jaccard相似度，将比较复杂度降至O(1)。

MinHash核心思想剖析

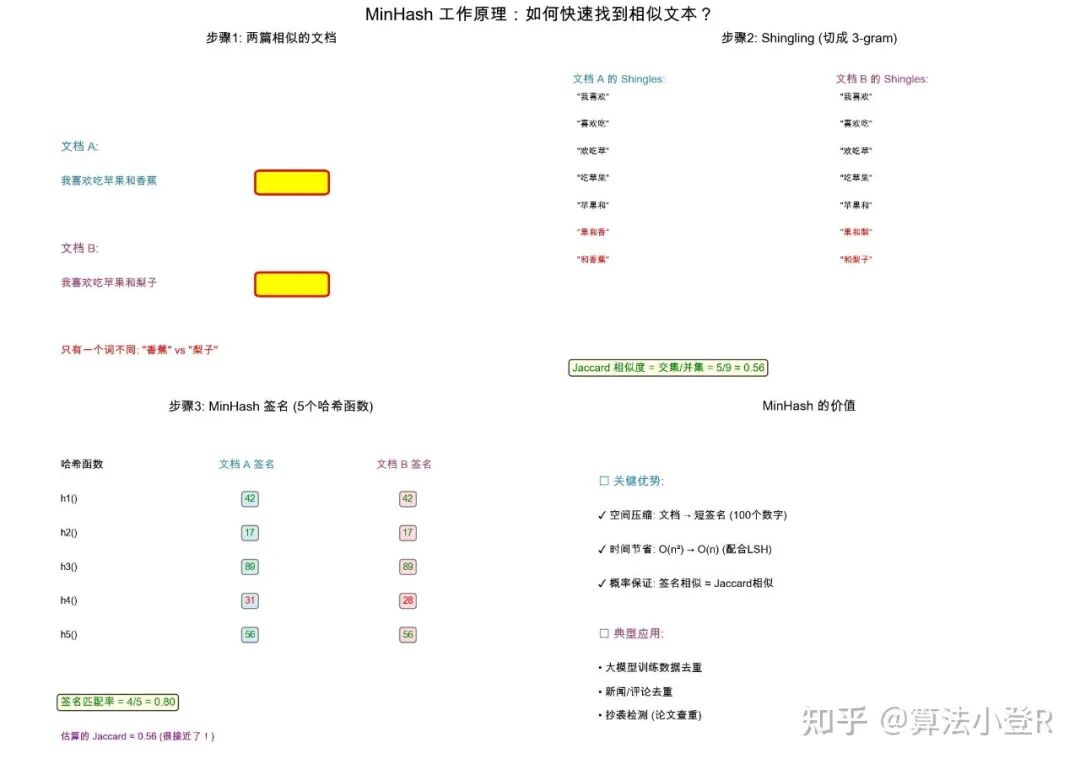
MinHash的巧妙之处在于用概率方法进行近似估算，主要分为两步：

1. 生成Shingle（文本切片）
首先，不直接使用单词，而是将文本转换为n-gram（连续n个字符的滑动窗口）。例如，对“我喜欢吃苹果”取3-gram：

shingles = {“我喜欢”， “喜欢吃”， “欢吃苹”， “吃苹果”}

这种方式能有效保留文本的词序信息。

2. 多次哈希并取最小值，生成签名
这是算法的关键步骤。假设我们准备100个不同的哈希函数（例如，通过改变随机种子实现）。对于集合中的每一个Shingle，都用这100个哈希函数计算其哈希值，对于每一个哈希函数，只记录所有Shingle计算出的最小值。

最终，我们会得到一个长度为100的数组，这就是该文本的MinHash签名。

其数学原理保证了：两个集合的Jaccard相似度，等于它们的MinHash签名在同一位置值相等的概率。
即：P(minhash_A[i] == minhash_B[i]) = Jaccard(A, B)
例如，若两个集合Jaccard相似度为0.8，则它们的MinHash签名在每个对应位置上相同的概率约为80%。

代码实现示例

以下是一个极简版的MinHash实现（仅使用hashlib库）：

import hashlib

def text_to_shingles(text, k=3):
    """将文本切割为k-gram集合"""
    return set(text[i:i+k] for i in range(len(text) - k + 1))

def minhash_signature(shingles, num_hashes=100):
    """生成MinHash签名"""
    signature = []
    for seed in range(num_hashes):
        min_hash = float('inf')
        for shingle in shingles:
            # 利用不同的seed模拟不同的哈希函数
            h = int(hashlib.md5((str(seed) + shingle).encode()).hexdigest(), 16)
            min_hash = min(min_hash, h)
        signature.append(min_hash)
    return signature

# 测试
text1 = “我喜欢吃苹果”
text2 = “我喜欢吃香蕉”
s1 = text_to_shingles(text1)
s2 = text_to_shingles(text2)

sig1 = minhash_signature(s1)
sig2 = minhash_signature(s2)

# 估算Jaccard相似度：统计签名中相同位置的值相等的比例
similarity = sum(1 for a, b in zip(sig1, sig2) if a == b) / len(sig1)
print(f“估算的相似度: {similarity:.2f}”)

运行上述代码，估算出的相似度应接近0.6，与理论Jaccard值基本吻合。这种基于哈希的方法为处理海量数据提供了可行思路。

实践中的注意事项

1. 哈希函数数量：初期仅使用10个哈希函数，导致估算误差波动较大。经验表明，通常需要100-200个哈希函数才能获得稳定的估计结果。
2. Shingle大小（k值）选择：
   • k值过小（如k=1），会丢失语义，“我喜欢你”和“你喜欢我”将被判为高度相似。
   • k值过大（如k=10），对细微修改过于敏感，容错性差。
   • 经验取值：中文文本通常取k=3，英文取k=5。
3. 内存优化：尽管MinHash签名已大幅压缩信息，但直接存储10亿条签名对内存仍是挑战。为此，需要结合LSH（局部敏感哈希） 建立索引，实现高效的近邻搜索，这是另一个技术重点。

适用场景与局限性

适用场景：

• 大规模文本去重（新闻、评论、爬虫数据清洗）。
• 抄袭或重复内容检测。
• 推荐系统中寻找相似用户或物品。

局限性：

• 数据量较小时（如几千条），直接计算Jaccard更简单准确。
• 无法理解语义。对于“苹果好吃”和“这水果真甜”这类语义相似但用词不同的句子，MinHash无能为力，需借助词向量或句向量等深度学习模型。

总结

MinHash算法的本质是：以可接受的精度误差为代价，换取存储空间和计算速度的巨大提升。

它通过巧妙的概率化哈希方法，将高维的集合比较问题转化为低维的数字签名比较，从而使得在超大规模数据集上进行快速相似性检测成为可能。如果你正面临海量数据去重或相似度计算的性能瓶颈，深入理解MinHash算法将会为你提供一个强有力的工具。