二分查找与哈希查找算法深度解析：工作原理、实现与应用场景对比

二分查找（Binary Search），又称折半查找，是一种基于有序数据集合的高效查找算法。其核心思想是每次比较都将查找范围缩小一半，从而在 O(log n) 的时间复杂度内快速定位目标元素。该算法要求数据预先排序，并适用于支持随机访问的结构如数组，相较于线性查找，在处理大规模数据时优势显著。

算法原理与步骤

二分查找遵循一套清晰的逻辑流程：

1. 初始化：确定查找范围的左边界 left 和右边界 right。
2. 计算中点：取中间位置 mid。为避免整数溢出，推荐使用 mid = left + (right - left) / 2 而非 (left + right) / 2。
3. 比较判断：将 arr[mid] 与目标值 target 进行比较：
   • 若相等，则查找成功，返回 mid。
   • 若 arr[mid] > target，说明目标值在左半部分，更新 right = mid - 1。
   • 若 arr[mid] < target，说明目标值在右半部分，更新 left = mid + 1。
4. 循环迭代：重复步骤2-3，直至 left > right（查找失败）或找到目标值。

核心特性:

• 前提条件：数据必须有序。
• 时间复杂度：O(log n)，处理大规模数据效率极高。
• 空间复杂度：迭代实现为 O(1)，递归实现为 O(log n)。
• 访问要求：依赖数据结构支持 O(1) 时间复杂度的随机访问（如数组）。

基础代码实现

以下是在 Java 中实现二分查找的两种方式：迭代与递归。

public class BinarySearch {
    // 迭代实现
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            // 避免整数溢出
            int mid = left + (right - left) / 2;

            // 找到目标值
            if (arr[mid] == target) {
                return mid;
            }
            // 在左半部分继续查找
            else if (arr[mid] > target) {
                right = mid - 1;
            }
            // 在右半部分继续查找
            else {
                left = mid + 1;
            }
        }

        // 未找到目标值
        return -1;
    }

    // 递归实现
    public static int binarySearchRecursive(int[] arr, int target, int left, int right) {
        if (left > right) {
            return -1;
        }

        int mid = left + (right - left) / 2;

        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] > target) {
            return binarySearchRecursive(arr, target, left, mid - 1);
        } else {
            return binarySearchRecursive(arr, target, mid + 1, right);
        }
    }

    // 测试
    public static void main(String[] args) {
        int[] arr = {2, 3, 4, 10, 40, 50, 70, 80};
        int target = 10;

        // 迭代方法
        int result = binarySearch(arr, target);
        if (result == -1) {
            System.out.println("元素 " + target + " 不存在于数组中");
        } else {
            System.out.println("元素 " + target + " 在数组中的索引为 " + result);
        }

        // 递归方法
        result = binarySearchRecursive(arr, target, 0, arr.length - 1);
        if (result == -1) {
            System.out.println("元素 " + target + " 不存在于数组中");
        } else {
            System.out.println("元素 " + target + " 在数组中的索引为 " + result);
        }
    }
}

优缺点分析

优点：

• 极高的查找效率（O(log n)）。
• 在大规模数据集上表现卓越。
• 实现逻辑清晰简单。
• 迭代版本无需额外空间。

缺点：

• 强制要求数据有序，维护有序性可能带来额外开销。
• 仅适用于数组等支持随机访问的结构。
• 对于小规模数据，优势不明显甚至可能慢于线性查找。

典型应用场景

二分查找的思想广泛应用于计算机科学的各个领域，是算法与数据结构学习的基石之一。

• 数据库索引：如 B+ 树等索引结构的查找过程基于二分思想。
• 边界查找：寻找第一个/最后一个等于（或大于/小于）目标值的位置。
• 数值计算：用于求解平方根等数学问题（二分法）。
• 特殊数组查找：在旋转排序数组中查找元素或最小值。

---

哈希查找（Hash Search），又称散列查找，采用完全不同的设计哲学。它通过哈希函数将数据元素的关键字直接映射到存储地址（数组下标），理想情况下可实现 O(1) 时间复杂度的查找，其核心是以空间换取时间。

算法原理与步骤

哈希查找的核心在于构建和管理哈希表：

1. 哈希函数设计：将关键字转换为数组索引。
2. 建表与插入：根据哈希值将元素存入哈希表对应位置。
3. 冲突解决：处理不同关键字映射到同一地址的“哈希冲突”（常用链地址法或开放寻址法）。
4. 执行查找：用相同哈希函数计算目标关键字地址，并在该位置（及冲突链）中查找。

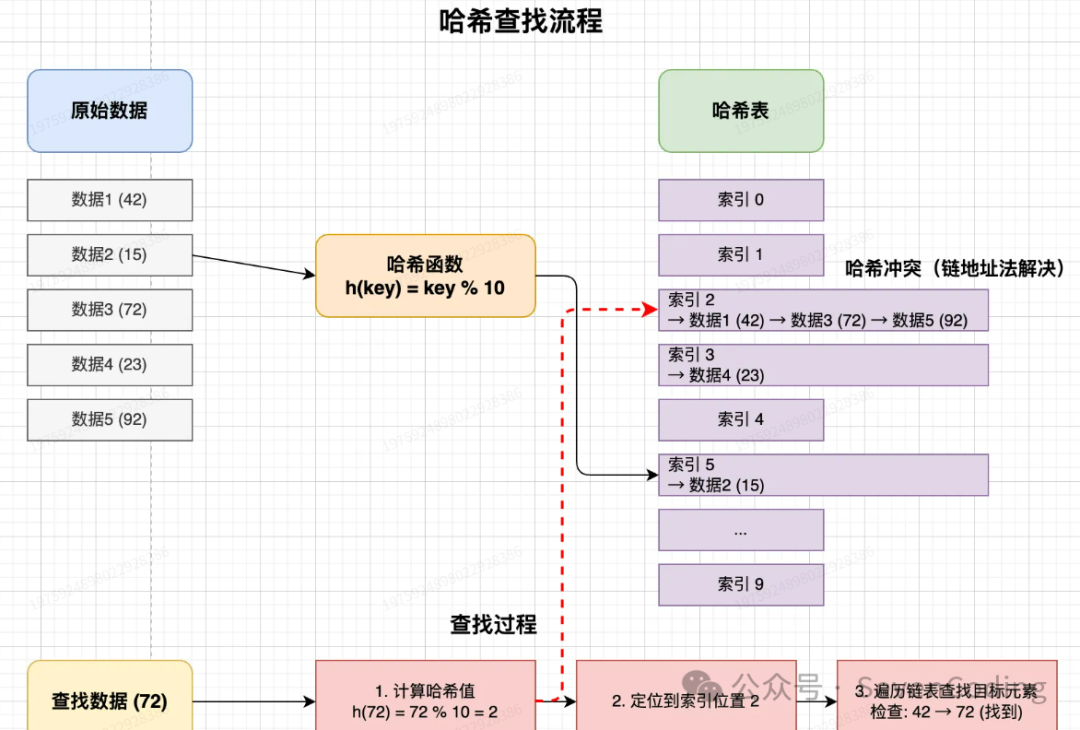
核心概念：

• 哈希函数：决定数据分布均匀性的关键。
• 哈希冲突：不可避免，处理方式直接影响性能。
• 负载因子：表中已存元素数与总容量的比值，触发扩容的阈值。
• 动态扩容：当负载因子过高时，需重建哈希表以维持性能。

基础代码实现（链地址法）

以下是一个使用链地址法解决冲突的简单哈希表实现。

public class HashSearch {
    // 哈希表节点类
    static class Node {
        String key;
        int value;
        Node next;

        public Node(String key, int value) {
            this.key = key;
            this.value = value;
            this.next = null;
        }
    }

    // 哈希表类
    static class HashTable {
        private Node[] buckets;
        private int capacity;
        private int size;
        private final float LOAD_FACTOR = 0.75f; // 负载因子阈值

        public HashTable(int capacity) {
            this.capacity = capacity;
            this.buckets = new Node[capacity];
            this.size = 0;
        }

        // 哈希函数
        private int hash(String key) {
            int hash = 0;
            for (char c : key.toCharArray()) {
                hash = (hash * 31 + c) % capacity;
            }
            return Math.abs(hash);
        }

        // 插入键值对
        public void put(String key, int value) {
            if ((float)size / capacity >= LOAD_FACTOR) {
                resize(2 * capacity);
            }

            int index = hash(key);
            Node newNode = new Node(key, value);

            // 如果桶为空，直接插入
            if (buckets[index] == null) {
                buckets[index] = newNode;
                size++;
                return;
            }

            // 处理哈希冲突，使用链地址法
            Node current = buckets[index];

            // 检查是否已存在相同的键
            while (current != null) {
                if (current.key.equals(key)) {
                    current.value = value; // 更新值
                    return;
                }
                if (current.next == null) {
                    break;
                }
                current = current.next;
            }

            // 在链表末尾添加新节点
            current.next = newNode;
            size++;
        }

        // 查找键对应的值
        public Integer get(String key) {
            int index = hash(key);
            Node current = buckets[index];

            // 遍历链表查找匹配的键
            while (current != null) {
                if (current.key.equals(key)) {
                    return current.value;
                }
                current = current.next;
            }

            // 未找到
            return null;
        }

        // 删除键值对
        public boolean remove(String key) {
            int index = hash(key);
            Node current = buckets[index];
            Node prev = null;

            // 查找目标节点
            while (current != null) {
                if (current.key.equals(key)) {
                    break;
                }
                prev = current;
                current = current.next;
            }

            // 未找到目标节点
            if (current == null) {
                return false;
            }

            // 删除节点
            if (prev == null) {
                buckets[index] = current.next;
            } else {
                prev.next = current.next;
            }

            size--;
            return true;
        }

        // 扩容并重新哈希
        private void resize(int newCapacity) {
            Node[] oldBuckets = buckets;

            // 创建新的哈希表
            buckets = new Node[newCapacity];
            capacity = newCapacity;
            size = 0;

            // 重新哈希所有元素
            for (Node bucket : oldBuckets) {
                Node current = bucket;
                while (current != null) {
                    put(current.key, current.value);
                    current = current.next;
                }
            }
        }
    }

    public static void main(String[] args) {
        HashTable hashTable = new HashTable(10);

        // 插入数据
        hashTable.put("apple", 5);
        hashTable.put("banana", 10);
        hashTable.put("orange", 15);
        hashTable.put("grape", 20);

        // 查找数据
        System.out.println("apple: " + hashTable.get("apple"));
        System.out.println("banana: " + hashTable.get("banana"));
        System.out.println("orange: " + hashTable.get("orange"));
        System.out.println("grape: " + hashTable.get("grape"));
        System.out.println("watermelon: " + hashTable.get("watermelon"));

        // 删除数据
        hashTable.remove("orange");
        System.out.println("After removing orange: " + hashTable.get("orange"));
    }
}

优缺点分析

优点：

• 平均情况下，查找、插入、删除的时间复杂度均为 O(1)。
• 不要求数据有序，使用灵活。
• 非常适合等值查询和动态数据集。

缺点：

• 存在哈希冲突，最坏情况下性能退化为 O(n)。
• 需要额外空间存储哈希表。
• 不支持高效的范围查询或顺序遍历。
• 性能受负载因子影响，需要动态扩容。

扩展与应用场景

哈希查找是构建高效键值存储的基石，其思想在数据库与中间件的索引实现中至关重要。

• 缓存系统：如 LRU Cache 的核心组件。
• 字典/映射结构：编程语言中 HashMap, dict 的基础。
• 去重操作：快速判断元素是否存在。
• 一致性哈希：用于分布式系统中，减少数据重新分布。
• 布隆过滤器：一种基于哈希的概率型数据结构，用于高效判断“可能存在”或“一定不存在”。

算法对比与总结

特性	二分查找 (Binary Search)	哈希查找 (Hash Search)
前提条件	数据必须有序	数据无需有序
时间复杂度	O(log n)	平均 O(1)，最坏 O(n)
空间复杂度	O(1) (迭代)	O(n)，需要额外哈希表空间
数据结构	数组等支持随机访问的结构	哈希表
适合操作	静态数据集的查找	动态数据集的查找、插入、删除
额外功能	支持范围查询、找上下界	主要支持等值查询

选择建议：

• 当数据静态有序且需要高频查找时，二分查找是经典选择。
• 当需要快速的等值查询、插入和删除，且不关心数据顺序时，哈希查找通常是更优解。
• 在实际系统如数据库中，两者常结合使用，例如在索引的局部使用二分查找。