从n-gram到Transformer：统计语言模型工作原理与AI大模型入门

语言是人类交流的复杂符号系统，其构成受到音韵、词法、句法等多重规则的约束，并承载丰富的语义。语言符号的一个重要特性是其不确定性：相同的意义可以由不同的形式表达，而相同的形式在不同的上下文中也可能产生不同的含义。因此，语言本质上是概率性的。语言模型的核心目标，正是为了准确计算和预测这些语言符号出现的概率。

从语言学的视角看，语言模型帮助计算机掌握语法、理解语义，从而完成各类自然语言处理任务。从认知科学和人工智能的发展历程看，从早期的规则模型（如ELIZA），到统计模型，再到如今的神经网络模型（如GPT-4），语言模型能力的跃迁也推动了机器智能的演进。本文将首先介绍基于统计方法的经典模型——n-grams语言模型，阐述其工作原理与局限性。

基于统计方法的语言模型：n-grams

统计语言模型通过分析语料库中语言符号的出现模式来学习并预测其概率。其中，n-grams模型通过直接统计词序列的频率来进行概率估计，是最具代表性的统计语言模型。

n-grams模型建立在马尔可夫假设和离散变量的极大似然估计之上。一个包含N个词的文本序列可以表示为 ( W_{1:N} = {w_1, w_2, ..., w_N} )。这里的“词”在更现代的模型中也可以是其他形式的Token。

n-grams模型的计算方法

n-gram指的是一个长度为n的词序列。n-grams模型通过计算语料库中n-gram与其对应的(n-1)-gram出现的相对频率，来估算整个文本序列 ( W_{1:N} ) 出现的概率。其核心计算公式如下：

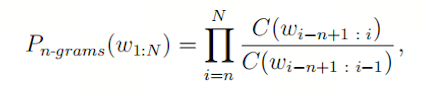
其中：

• ( C(w{i-n+1:i}) ) 表示词序列 ( {w{i-n+1}, ..., w_i} ) 在语料库中出现的次数。
• ( C(w{i-n+1:i-1}) ) 表示词序列 ( {w{i-n+1}, ..., w_{i-1}} ) 在语料库中出现的次数。

参数 n 是一个可变量：

• 当 n=1 时，称为 unigram，它不考虑上下文关系，公式简化为 ( P(w_i) = \frac{C(wi)}{C{total}} )，其中 ( C_{total} ) 是语料库总词数。
• 当 n=2 时，称为 bigram，它只考虑前一个词，公式为：
  
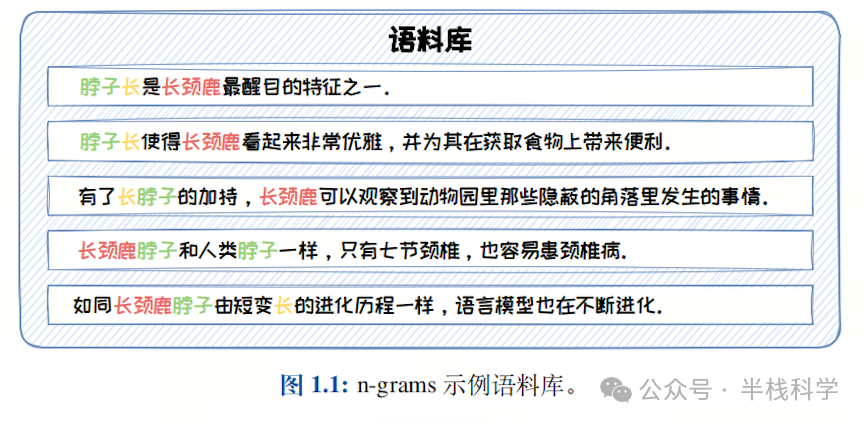
• 当 n=3 时，称为 trigram，以此类推。

实例解析：Bigram模型

假设有一个包含5个句子的微型语料库（如图1.1所示）。基于此语料库，我们用bigram模型来计算文本“长颈鹿脖子长”（由三个词构成）出现的概率：

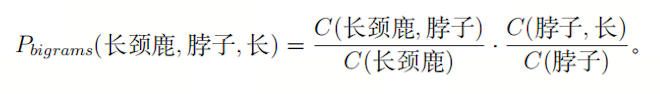
根据语料库统计：( C(\text{长颈鹿}) = 5 )， ( C(\text{脖子}) = 6 )， ( C(\text{长颈鹿, 脖子}) = 2 )， ( C(\text{脖子, 长}) = 2 )。代入公式计算：

这个例子揭示了一个关键点：即使“长颈鹿脖子长”这个完整句子从未在语料库中出现过，bigram模型依然能够通过组合子序列的概率，给出一个非零的估计值。这体现了统计模型相对于早期基于规则方法的核心优势——泛化能力。

n-gram模型的挑战与权衡

然而，这种泛化能力会随着 n 的增大而减弱。如果我们使用trigram模型来计算同一个句子，就会遇到“零概率”问题：

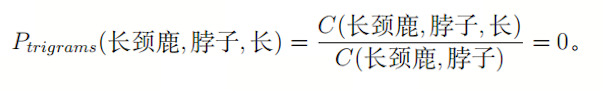
因为“长颈鹿脖子”这个词对在语料库中并未出现，导致概率为零，进而整个句子的概率也为零。这种现象被称为数据稀疏性问题。

因此，在n-grams模型中，n 的选择是一个关键的权衡：

• n 太小（如unigram）：模型无法捕捉有意义的上下文信息，表达能力弱。
• n 太大（如4-gram, 5-gram）：模型过于“死记硬背”，对训练数据拟合能力强，但泛化能力急剧下降，极易出现零概率问题。

通常，bigram和trigram是实践中较常使用的折中选择。对于零概率问题，可以通过平滑技术（如拉普拉斯平滑、古德-图灵估计等）进行缓解。

n-grams模型的统计学原理

从统计学视角看，n-grams模型是在n阶马尔可夫假设下，对语料库中词序列出现概率的极大似然估计。

n阶马尔可夫假设是指：一个词的出现概率仅依赖于它前面的n-1个词。

离散型随机变量的极大似然估计是通过统计频率来估计概率。

基于以上定义，文本序列 ( W{1:N} ) 的概率 ( P(w{1:N}) ) 根据链式法则为：

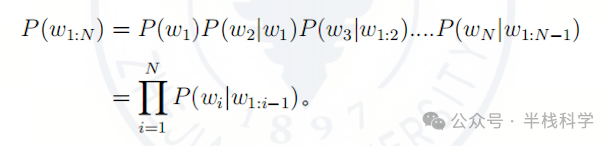
在n阶马尔可夫假设下，每一项被简化为：

最终，整个序列的概率可以表示为：

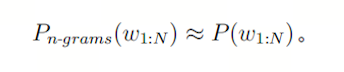
这正是之前给出的n-grams计算公式。因此，n-grams模型的参数 ( P_{MLE}(wi | w{i-n+1:i-1}) ) 就是对条件概率 ( P(wi | w{i-n+1:i-1}) ) 的极大似然估计：

总结与演进

n-grams语言模型作为早期自然语言处理的基石，通过简洁的统计方法赋予计算机初步的“语言直觉”，但其严重的数据稀疏性和有限的上下文记忆能力（仅n-1个词）限制了其性能。随着计算能力的提升，基于神经网络的语言模型 逐渐成为主流。它们不再依赖显式的频率统计，而是通过训练神经网络从海量数据中自动学习复杂的语言规律和长距离依赖关系，泛化能力得到质的飞跃，最终催生了如今强大的大语言模型（LLM）。从循环神经网络到Transformer架构的演进，正是语言模型能力不断突破的关键路径。