Transformer架构中LayerNorm详解：为何大模型舍弃BatchNorm选择LayerNorm

观察 BERT、GPT 到如今 Qwen 系列的架构演进，你会发现 LayerNorm 是极少数被完整继承下来的核心组件。

即便是在追求极致推理性能的今天，大模型也只是将 LN 升级为了计算效率更高的 RMSNorm，而非更换其他方案。

这种高度的一致性背后，隐藏着 Transformer 处理序列数据时的底层逻辑。

这也引出了一个经典的面试问题：为什么在图像领域统治多年的 BatchNorm （BN），在 Transformer 架构里却被 LayerNorm 挤下了神坛？

这篇文章我们不堆公式，用直观解释把这背后的道理讲清楚。文末会单独拆解一下目前最流行的 RMSNorm 代码实现。

深度神经网络的内部协变量偏移问题

深度神经网络一直面临一个核心痛点：随着网络层数的加深，参数的微小扰动会在层层传递中被放大，导致输出分布剧烈震荡。

这在学术上被称为内部协变量偏移（Internal Covariate Shift）。简单理解，就是蝴蝶效应，第一层的参数变一点，最后一层的分布就飘到了十万八千里外。

后果就是：梯度极其不稳定。要么梯度消失（模型学不动），要么梯度爆炸（Loss 飞出天际）。

为了给这训飞了的模型套上缰绳，Norm 层应运而生。它强制把每一层的输入拉回到标准的正态分布。

但问题来了，怎么归一化？这里就涉及到了 Transformer 和 CNN 根本性质的不同。

BatchNorm (BN) 为何在 NLP 中水土不服？

BatchNorm 的逻辑是沿着 Batch 维度进行归一化。它假设一个 Batch 里的图片能代表整体分布。这在 CV 里没问题，因为图片尺寸通常是固定的（比如 224x224）。

在深度学习框架里，沿着某个维度归一化的意思是：把这个维度里的所有数抓出来，求平均，最后这个维度就消失了。

但是在 NLP 任务中，Transformer 面临着两个 BN 无法解决的硬伤：

1. 变长序列与 Padding 的干扰

NLP 数据天然是变长的。为了凑成一个 Batch，短句子后面必须补 0 (Padding)。

如果使用 BN，这些无意义的“0”会强行参与均值和方差的计算。这就像统计班级平均分时，把没来考试的人都算作 0 分，直接拉低了整体的统计分布，导致模型学到的特征产生巨大偏差。

举例分析：

假设我们的文本训练语料是：

[
  [为什么天是蓝色的？因为瑞利散射效应。], # 长度18
  [小蜜蜂会冬眠吗？密封会冬眠。], # 长度 14
  [飞机是怎么起飞的？利用发动机产生巨大推力起飞。], # 长度 23
]

每个 token (汉字) 的 hidden_size 是 1024，那么输入语料的维度是：[3, 23, 1024]。为了让 GPU 能一次性并行处理这三句话，我们必须把短句子补齐（Padding）成长度 23。

• 第一句（长度18）：...瑞利散射效应。 -> 后面补 5 个全是 0 的 Token。
• 第二句（长度14）：...密封会冬眠。 -> 后面补 9 个全是 0 的 Token。
• 第三句（长度23）：...产生巨大推力起飞。 -> 最长，不用补。

BatchNorm 会把 Batch 里所有样本在同一个位置、同一个特征通道上的数值抓出来做平均。

场景一：无 Padding 的位置 (第 2 个词)
假设我们计算索引 256 特征维度，代表“实体名词的激活程度”。三句话在该位置的值分别为 0.2 (‘什’)， 0.8 (‘蜜’)， 0.8 (‘机’)。BN 计算的均值为 (0.2+0.8+0.8)/3 = 0.6。虽然把不同语义的词强行平均，但至少数据是真实的。

场景二：有 Padding 的位置 (第 20 个词)
假设我们计算索引 128 特征维度，代表“力量/动作的猛烈程度”。在该位置，前两句是 Padding (值为0)，第三句是实词“力”（值为0.9）。BN 计算的均值为 (0.0+0.0+0.9)/3 = 0.3。

• 对于“力”字来说： 原本 0.9 的高强度特征被稀释成了 0.3，特征被削弱。
• 对于 Padding 来说： 本来是 0，减去均值 0.3 后变成 -0.3，无中生有地引入了噪声。

当 Batch Size 很大，且包含大量短句时，有意义的特征值会被淹没在“0”的海洋里。这就是 BN 在处理变长序列补 0 时失效的根本原因。

2. 训练与推理的割裂

最直观的矛盾在于推理阶段的 Batch Size 通常固定为 1，这与训练时通过大批量样本获取统计特性的模式完全脱节，导致 BN 在推理时只能依赖训练期积累的全局统计量（Running Mean/Var）。

而序列模型各时间步分布的不一致性使得这些统计量在面对超长文本或罕见样本时极易失效，最终可能引发模型性能的衰退。

BatchNorm 的公式：

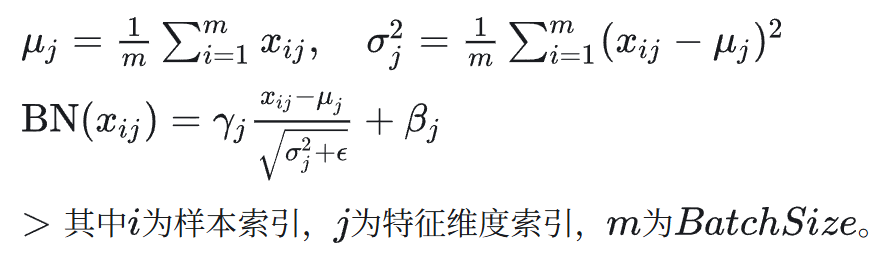
LayerNorm (LN) 如何成为 LLM 的救星？

Transformer 选择 LayerNorm，是因为它采用了一种完全不同的归一化策略：样本内独立 (Instance Independence)。

它的逻辑非常简单粗暴：“我不看别人，只看我自己。”

不管 Batch Size 是大是小，也不管这句话后面补了多少个 0，LayerNorm 只在当前样本的 Feature 维度上进行归一化。

• 优势一：独立性。 单一样本的语义理解，不受 Batch 里其他句子的干扰。
• 优势二：一致性。 训练和推理使用完全相同的计算逻辑，不需要维护全局统计量，完美适应变长序列。

场景分析：有 Padding 的位置 (第 20 个词)

• 第一句 (Padding): LN 拿到一个全 0 的向量 [0,0,...,0]，它就在这 1024 个 0 内部算均值方差。
• 第二句 (Padding): 同理，在自己内部计算，不干扰他人。
• 第三句 (‘力’): LN 拿到“力”字对应的1024维特征向量 [0.9, -0.5, 2.1, ...]。它只计算这 1024 个数的均值（例如 0.4）和方差，并用其进行归一化。结果完全不受前两句 Padding 的影响。

总结对比：
如果说 BatchNorm 是大锅饭，一人点菜（Padding），全桌买单；那么 LayerNorm 就是“分餐制”，自己吃自己的盘中餐，无论旁边坐的是谁，都不会影响你这一餐的营养摄入。正是这种设计，让 Transformer 能够在 Micro-Batch 极小的情况下依然稳定训练，这对于动辄显存爆炸的大模型训练至关重要。

LayerNorm 的公式：

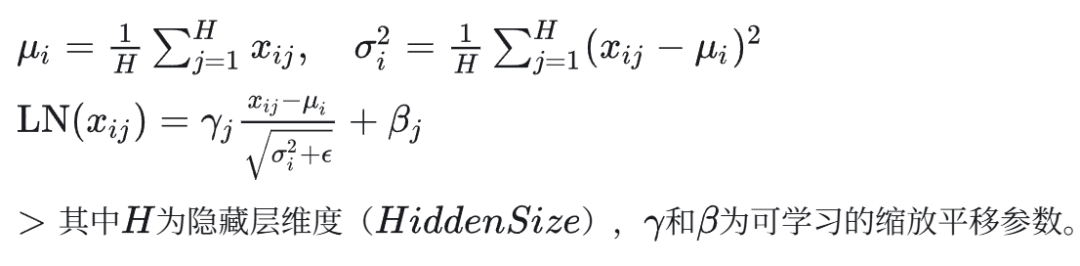
架构演进：从 Post-Norm 到 RMSNorm

LayerNorm 确立地位后，并没有停止进化。目前的 LLM 架构演进经历了三个阶段：

1. 初始形态：Post-Norm (原始 Transformer)

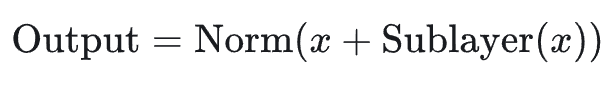
《Attention is All You Need》论文采用了这种结构。理论上很美，但实战中极难训练，需要极其小心地设计 Warmup 策略，否则梯度极易在反向传播早期炸裂。

2. 稳定形态：Pre-Norm

为了解决深层网络的训练难题，业界将 Norm 移到了残差块的“主干道”之前。这极大地提升了梯度的流通性，让训练几百层的超深网络成为可能。虽然理论上限略有牺牲，但换来了工程上无可比拟的稳定性。

3. 最新形态：RMSNorm (Llama/Qwen 时代)

这是目前的主流选择。研究团队发现，LayerNorm 中的“减均值（Centering）”操作对模型性能贡献微乎其微，但消耗了计算资源。
RMSNorm (Root Mean Square Norm) 直接砍掉了减均值步骤，只做缩放（Scaling）。
这不仅保留了归一化的核心效果，还节省了计算开销。在万亿 token 的训练规模下，这点微小的算力节省累积起来就是巨大的成本优势。

Qwen3-4B 的 Dense 架构，采用了 Pre-RMSNorm

代码解析：手搓一个高效的 RMSNorm

既然 RMSNorm 是目前的业界主流，我们来看看它是如何在 PyTorch 中高效实现的。这不仅仅是公式的翻译，更涉及到了大模型训练中的精度对齐技巧。

import torch
from torch import nn

class RMSNorm(nn.Module):
    def __init__(self, hidden_size: int, eps: float = 1e-6) -> None:
        super().__init__()
        # eps 防止除以零的数值稳定性保护
        self.eps = eps
        # 可学习的缩放参数 gamma (weight)，初始化为1
        self.weight = nn.Parameter(torch.ones(hidden_size))

    @torch.compile
    def rms_forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        核心公式:
              x * weight
        y = -----------------
            sqrt(mean(x²) + ε)
        """
        # [关键细节 1] 精度对齐
        # 输入 x 通常是 bfloat16 (半精度) 以节省显存
        # 但在计算均方根 (RMS) 这种统计量时，必须强制转为 float32 (全精度)
        # 否则微小的精度溢出或下溢会导致 Loss 震荡
        orig_dtype = x.dtype
        x = x.float() 
        # 计算均方根的平方部分：x^2 -> mean
        var = x.pow(2).mean(dim=-1, keepdim=True)
        # 计算归一化结果：x * rsqrt(var + eps)
        # rsqrt 是 1/sqrt 的一种硬件加速写法
        x.mul_(torch.rsqrt(var + self.eps))
        # [关键细节 2] 转回原精度并应用可学习参数
        # 归一化后，转回 bfloat16 并乘上缩放系数 weight
        x = x.to(orig_dtype).mul_(self.weight)
        return x

    # 融合了残差连接的高效实现版本
    # 在大模型推理中，常将 Residual + Norm 算子融合以减少显存读写次数
    @torch.compile
    def add_rms_forward(self, x: torch.Tensor, residual: torch.Tensor) -> tuple[torch.Tensor, torch.Tensor]:
        orig_dtype = x.dtype
        # 先做残差连接：Pre-Norm 结构
        x = x.float().add(residual.float())
        residual = x.to(orig_dtype) # 更新 residual 供下一层使用
        # 这一步逻辑同上：RMS 归一化
        var = x.pow(2).mean(dim=-1, keepdim=True)
        x.mul_(torch.rsqrt(var + self.eps))
        x = x.to(orig_dtype).mul_(self.weight)
        return x, residual

    def forward(self, x: torch.Tensor, residual: torch.Tensor | None = None
        ) -> tuple[torch.Tensor, torch.Tensor]:
        if residual is None:
            return self.rms_forward(x)
        else:
            return self.add_rms_forward(x, residual)

代码要点解析：

1. 混合精度训练： 代码中反复出现的 x.float() 和 x.to(orig_dtype) 并非多此一举。在大模型训练中，权重通常用 bfloat16 存储以节省显存，但在进行 Norm 这种涉及除法和开方的敏感操作时，必须切回 float32 保证数值稳定性，这是PyTorch 深度学习中保障训练稳定的常见技巧。
2. 算子融合： add_rms_forward 方法体现了工程优化的思维。将 Add（残差）和 Norm 操作放在一个函数里，并配合 @torch.compile 装饰器，可以最大程度减少 GPU 内存的读写带宽压力（Memory Wall），提升推理效率。

来源：https://zhuanlan.zhihu.com/p/1985480142802412942