本文旨在深入解析IEEE 754浮点数标准,涵盖其基本构成、特殊数值表示、单双精度格式差异,并通过C++代码示例演示其二进制表示与计算特性。理解这些内容是进行精确数值计算和避免潜在陷阱的基础。
一、IEEE 754浮点数核心概念
一个标准的浮点数由三部分组成:
- 符号位 (Sign):决定数值的正负。
- 指数位 (Exponent):决定数值的量级。
- 分数位/尾数位 (Fraction/Mantissa):决定数值的精度。
理解以下几点至关重要:
- 非均匀分布:IEEE 754浮点数在实数轴上并非均匀分布,只能精确表示有限数量的实数。例如,十进制数
0.1 就无法被精确表示。
- 隐含的“1”:对于正规数 (Normal Number),其尾数部分默认隐含一个前导的“1”(即格式为
1.xxxx)。
- 正零与负零:标准中定义了正零 (
S=0, E=0, F=0) 和负零 (S=1, E=0, F=0)。一些数学函数(如 atan2)对两者的处理结果不同(例如返回 π 和 -π)。
- 亚正规数 (Subnormal Number):当指数位全为0且尾数位不为0时,表示非常接近零的数。这类数有助于实现渐进下溢 (Gradual Underflow),避免突然归零带来的精度损失。
- 舍入模式:标准定义了四种舍入模式,用于处理无法精确表示的结果。
- 计算异常:
- 上溢 (Overflow):结果超出可表示的最大值。需要特别关注,常见于大整数转浮点数或计算范数(如
sqrt(x² + y²))时。
- 下溢 (Underflow):结果小于可表示的最小正规数。危害相对较小,通常会归零或转为亚正规数。
- 特殊值的比较:
Infinity > 1 的结果为真。NaN 与任何值(包括其自身)的比较操作(>, ==, <)结果均为假。
- 亚正规数处理策略:通常有“刷新到零 (Flush to Zero)”和“渐进下溢”两种方式。亚正规数计算可能显著影响性能,部分编译器允许通过选项控制其处理方式。渐进下溢在需要高精度的场景(如数值微分)中更有优势。
二、单精度与双精度浮点数
单精度浮点数 (float, 32位)
单精度浮点数的表示范围如下图所示:
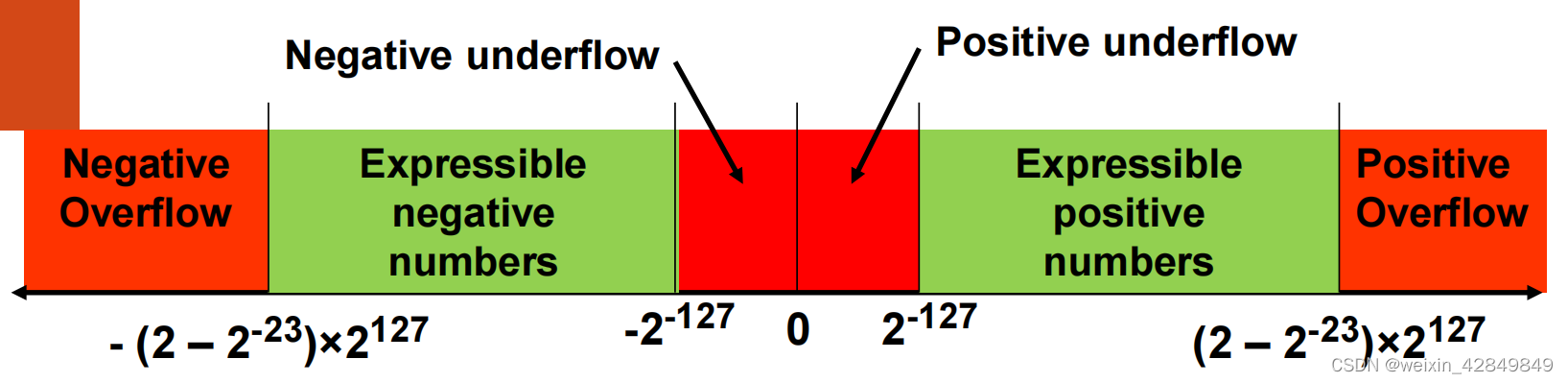
其具体格式与关键参数如下:
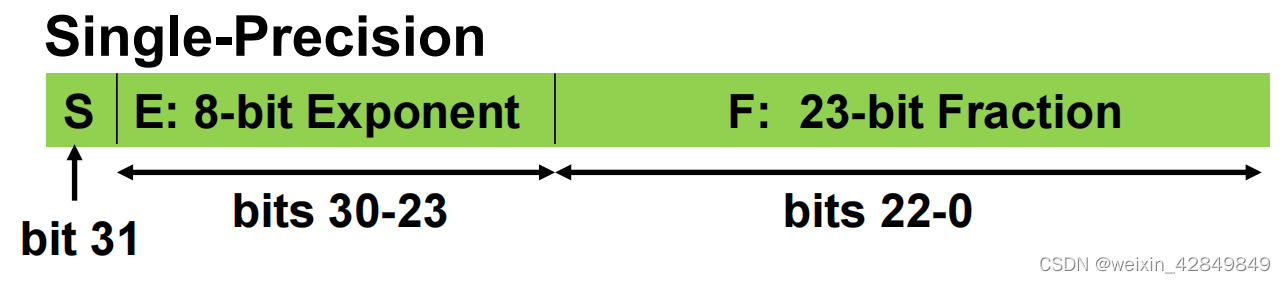
| 参数 |
说明 |
| 偏移 (Bias) |
127 |
| 指数 E 范围 |
[1, 254] (0 和 255 为特殊值保留) |
| 数值范围 |
\(2^{-126}\) 至 \(2^{127}\) |
下表展示了一些特殊单精度数值的二进制表示(可通过 std::numeric_limits<float> 获取):
| 浮点数 |
二进制表示 (32位) |
| 0 |
00000000000000000000000000000000 |
| -0 |
10000000000000000000000000000000 |
| 1 |
00111111100000000000000000000000 |
| -1 |
10111111100000000000000000000000 |
| 机器精度 epsilon |
00110100000000000000000000000000 |
| 1 + epsilon |
00111111100000000000000000000001 |
| 最小正规正数 min |
00000000100000000000000000000000 |
| 最大正数 max |
01111111011111111111111111111111 |
| 最小正亚正规数 denorm_min |
00000000000000000000000000000001 |
| 正无穷大 infinity |
01111111100000000000000000000000 |
| 信号NaN sNaN |
01111111101000000000000000000000 |
| 静默NaN qNaN |
01111111110000000000000000000000 |
双精度浮点数 (double, 64位)
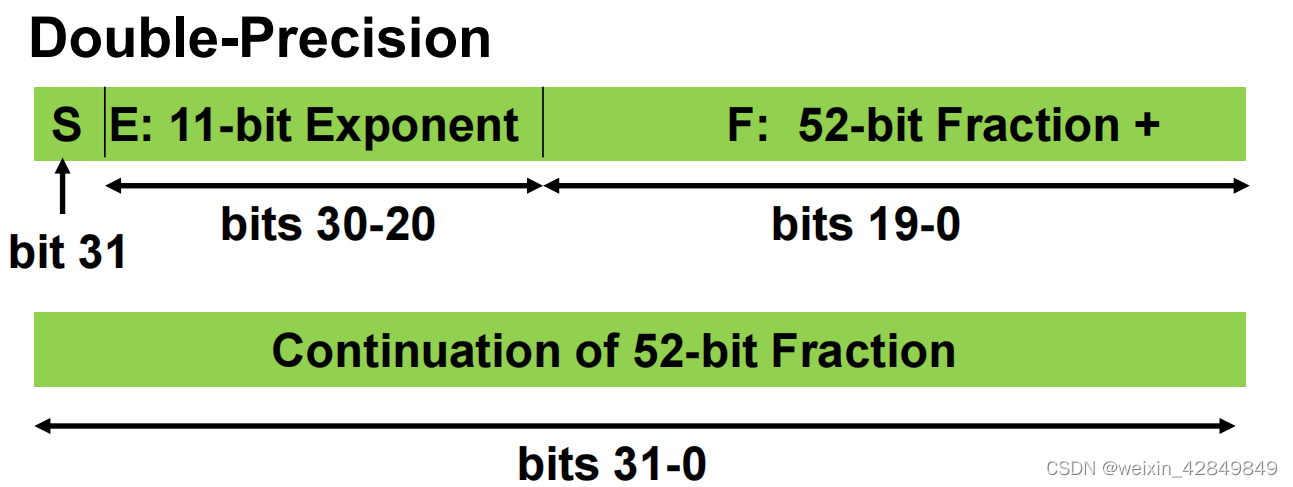
| 参数 |
说明 |
| 偏移 (Bias) |
1023 |
| 指数 E 范围 |
[1, 2046] (0 和 2047 为特殊值保留) |
| 数值范围 |
\(2^{-1022}\) 至 \(2^{1023}\) |
部分特殊双精度数值的二进制表示如下:
| 浮点数 |
二进制表示 (64位) |
| 0 |
0000000000000000000000000000000000000000000000000000000000000000 |
| -0 |
1000000000000000000000000000000000000000000000000000000000000000 |
| 1 |
0011111111110000000000000000000000000000000000000000000000000000 |
| -1 |
1011111111110000000000000000000000000000000000000000000000000000 |
| 机器精度 epsilon |
0011110010110000000000000000000000000000000000000000000000000000 |
| 1 + epsilon |
0011111111110000000000000000000000000000000000000000000000000001 |
| 最小正规正数 min |
0000000000010000000000000000000000000000000000000000000000000000 |
| 最大正数 max |
0111111111101111111111111111111111111111111111111111111111111111 |
| 正无穷大 infinity |
0111111111110000000000000000000000000000000000000000000000000000 |
| 信号NaN sNaN |
0111111111110100000000000000000000000000000000000000000000000000 |
| 静默NaN qNaN |
0111111111111000000000000000000000000000000000000000000000000000 |
三、浮点数加减法运算流程
浮点数的加减运算并非简单的位操作,其流程涉及对阶、尾数运算、规格化和舍入等步骤。下图清晰地展示了这一核心流程:
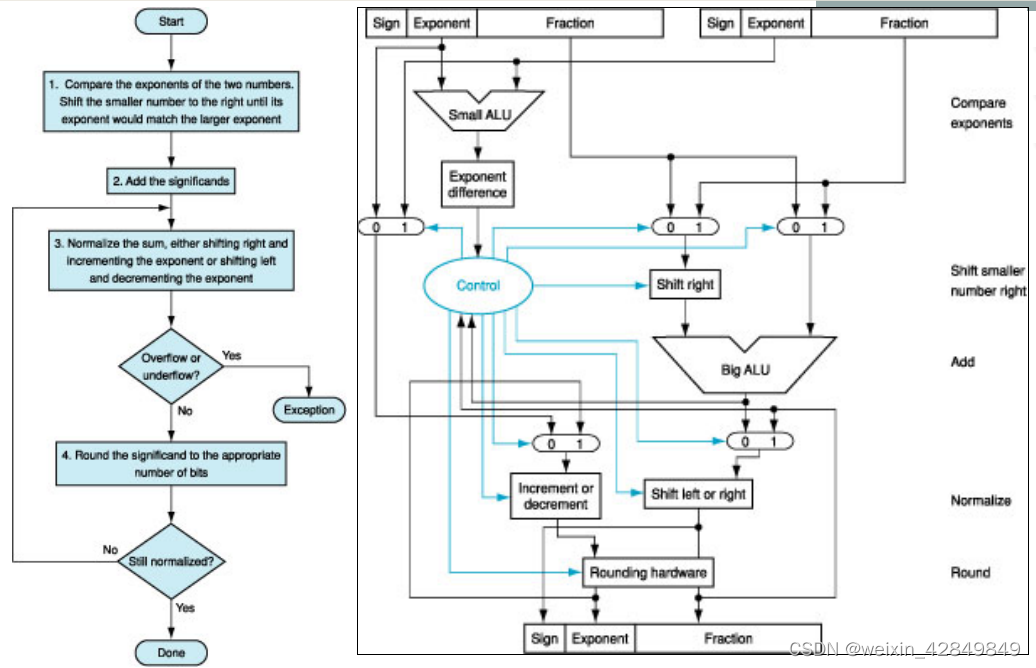 浮点数加法运算流程图。核心步骤包括:比较指数、对齐尾数、相加、规格化结果并进行舍入。
浮点数加法运算流程图。核心步骤包括:比较指数、对齐尾数、相加、规格化结果并进行舍入。
四、C++代码实践:探查浮点数表示与特性
以下C++程序演示了如何获取并打印浮点数的二进制表示、极限值,并验证其特殊行为。这有助于在具体的编程实践中加深理解。
/************************************
测试IEEE浮点数标准、表示形式等
*************************************/
#include <cmath>
#include <iostream>
#include <bitset>
#include <limits>
#include <type_traits>
#include <cstdint>
#include <sstream>
#include <string>
using namespace std;
// 函数模板:以二进制形式输出任何类型的位模式
template<typename R>
std::ostream &dump_bits(const R x, std::ostream &os=std::cout) {
uint8_t *u8 = (uint8_t *)&x;
string s("");
// 假设小端序
for(int i = sizeof(R)-1; i >= 0; --i) {
std::bitset<8> b(u8[i]);
s += b.to_string();
}
os << s;
return os;
}
// 函数模板:以十六进制浮点格式输出
template<typename R>
std::ostream &dump_hex(const R x, std::ostream &os=std::cout) {
os << std::hexfloat << x << std::defaultfloat;
return os;
}
// 函数模板:打印数值类型的极限值
template<typename T>
void print_limits() {
using flimits = numeric_limits<T>;
cout << "radix:\t" << flimits::radix << "\n";
cout << "min_exponent:\t" << flimits::min_exponent << "\n";
cout << "max_exponent:\t" << flimits::max_exponent << "\n";
cout << "digits:\t" << flimits::digits << "\n";
cout << "digits10:\t" << flimits::digits10 << "\n";
cout << "epsilon:\t" << flimits::epsilon() << "\n";
cout << "inf:\t" << flimits::infinity() << "\n";
cout << "qNan:\t" << flimits::quiet_NaN() << "\n";
cout << "sNan:\t" << flimits::signaling_NaN() << "\n";
cout << "min:\t" << flimits::min() << "\n";
cout << "max:\t" << flimits::max() << "\n";
}
// 函数模板:打印特殊值的二进制和十六进制表示
template<typename T>
void print_bits_and_hex() {
static_assert(std::is_same_v<T,float> || std::is_same_v<T,double> || std::is_same_v<T,long double>);
using flimits = numeric_limits<T>;
auto dump = [](std::ostream &os, string name, const T &x) -> std::ostream & {
os << name << "\t";
dump_bits(x, os);
os << " ";
dump_hex(x, os);
os << "\n";
return os;
};
dump(cout, "infinity", flimits::infinity());
dump(cout, "sNaN", flimits::signaling_NaN());
dump(cout, "qNaN", flimits::quiet_NaN());
dump(cout, "0", T(0.0));
dump(cout, "-0", T(-0.0));
dump(cout, "1", T(1));
dump(cout, "-1", T(-1));
dump(cout, "eps", flimits::epsilon());
dump(cout, "1+eps", flimits::epsilon() + T(1));
dump(cout, "min", flimits::min());
dump(cout, "max", flimits::max());
dump(cout, "denorm_min", flimits::denorm_min());
}
int main(int argc, char **argv) {
cout << R"(
=========================================================================
单精度浮点数(float) limits
=========================================================================)" << "\n";
print_limits<float>();
cout << R"(
=========================================================================
双精度浮点数(double) limits
=========================================================================)" << "\n";
print_limits<double>();
cout << R"(
=========================================================================
单精度浮点数(float)二进制模式
=========================================================================)" << "\n";
print_bits_and_hex<float>();
cout << R"(
==========================================================================
双精度浮点数(double)二进制模式
==========================================================================)" << "\n";
print_bits_and_hex<double>();
cout << R"(
==========================================================================
长精度浮点数(long double)二进制模式
==========================================================================)" << "\n";
print_bits_and_hex<long double>();
// 验证特殊值的比较与运算行为
cout << "\n特殊值行为验证:\n";
cout << ((numeric_limits<float>::infinity() > 1.0f) ? "inf > 1 成立\n" : "inf <= 1 成立\n");
cout << "inf / 2 = " << numeric_limits<float>::infinity() / 2.0f << "\n";
cout << "(NaN > 1) = " << (numeric_limits<float>::quiet_NaN() > 1.0f) << "\n";
cout << "(NaN < 1) = " << (numeric_limits<float>::quiet_NaN() < 1.0f) << "\n";
cout << "(-0.0 < 0.0) = " << (-0.0f < 0.0f) << "\n";
return 0;
}
// 编译命令: g++ -std=c++17 ieee754_demo.cpp
程序运行后会输出详细的浮点数极限信息、二进制表示,并验证特殊值的比较规则。