0. 引言
本篇讲讲 DeepSeek 在 MoE(Mixture-of-Experts)上的演进过程。DeepSeek 是 MoE 稀疏模型的忠实玩家:主版本模型从 DeepSeekMoE(V1)到 DeepSeek V3,一直坚持 MoE 的技术路线,并持续做出一些创新。本文参考 paper 并结合源码阅读,梳理 MoE 的演进过程与具体实现。
想系统讨论模型训练与并行通信这类工程问题,也可以到 云栈 找相关话题一起交流。
1. 简述 MoE 的发展历程
先简单回顾 MoE 的发展历史。早在 1991 年,一篇名为《Adaptive Mixtures of Local Experts》的工作最早提出了 Mixture of Experts 的原型框架(图1)。直到今天,MoE 的核心框架仍基本保持这种形式。
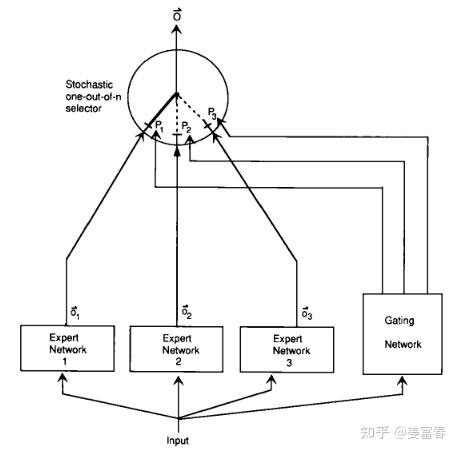
MoE(Mixture of Experts)是一种网络层结构,网络层主要包括三部分:
- 专家网络(Expert Network):通常是前馈网络。逻辑上一个专家擅长处理一类子任务。所有专家都接受相同输入,进行特定计算,产出不同输出。
- 门控网络(Gating Network):接收与专家网络相同的输入,输出专家偏好的权重,用于表示对某个输入各专家的重要程度。
- 选择器(selector):根据专家权重做专家选择的策略。可选择权重最高的 Top1 或 TopK 专家,融合得到最终结果。
随后一段时间主要由 Google 主导 MoE 的发展。进入 Transformer 时代后,2020 年 Google 发表《GShard》,将模型训练到 600B 规模,并刻画了 Transformer 上做 MoE 的经典设计,主要包括 Transformer MoE 层设计和辅助负载均衡损失。
MoE 层替换 Transformer 的 FFN 层。对一个 token:分别通过门控网络和专家网络计算门控值与专家输出,再用门控值加权多个专家输出得到最终结果:
$$[g_{s,1}, g_{s,2},..., g_{s,E}] = softmax(w_g. x_s)$$
$$FFN_e(x_s) = W_{o_e} . ReLU(W_{i_e} . x_s)$$
$$y_s = \sum_{e=1}^E g_{s,e} . FFN_e (x_s)$$
注:这里的专家是 token 级专家,而不是样本粒度。每个 token 都会做专家路由。专家是 稀疏激活 的,会根据门控值取 TopK 个专家融合计算最终结果。GShard 最多激活权重最高的 2 个专家。
1.2 负载均衡:辅助损失
引入负载均衡损失(aux_loss),目的是解决多专家 token 分布不均的问题。如果完全按门控权重选取 TopK 专家,容易导致训练过程负载不均衡:
- 大多数 token 被分配到少数专家:通信繁忙造成拥堵,训练速度变慢;
- 其他专家得不到充分训练。
如何定义负载均衡的辅助损失?
令每个专家收到的 token 占总 token 的比例为:
$$\frac{c_{1}} {S}, \frac{c_{2}}{S}, ..., \frac{c_{E}}{S}$$
其中
$$S$$
表示 token 数量,
$$\{1, 2, ..., E\}$$
表示专家集合,
$$c_e$$
表示第
$$e$$
个专家接收的 token 数。
如果负载均衡,每个专家收到 token 一样多,即
$$\frac{c_i}{S}$$
值相等。可用比例平方和描述负载均衡损失:
$$\mathcal{l}_{aux} = \frac{1} {E} \sum_{e=1}^E(\frac {c_{e}}{S})^2$$
但上式中的
$$\frac{c_e}{S}$$
来自 TopK 的 hard 路由,和参数无关,不可梯度更新。作者用每个专家的门控权重均值
$$m_e$$
作为
$$\frac{c_e}{S}$$
的近似:
$$m_{e} = \frac{1}{S} \sum _{s=1}^Sg_{s,e}$$
其中
$$g_{s,e}$$
为针对 token
$$s$$
计算得到的专家
$$e$$
的门控权重。
接着引出两个关键问题:
问题1:为什么
$$m_e$$
可以看作 $$\frac{c_e}{S}$$
的近似?
答:直观上,若极端情况下每个 token 最多分配给 1 个专家,可把被激活专家权重看作 1,其他为 0,则对专家 $$e$$
有 $$m_e = \frac{c_e}{S}$$
。从定义看,$$m_e$$
表示 token 集合分配给专家 $$e$$
的概率,是 soft 形式;而 $$\frac{c_e}{S}$$
是 TopK hard 形式。两者通常近似。
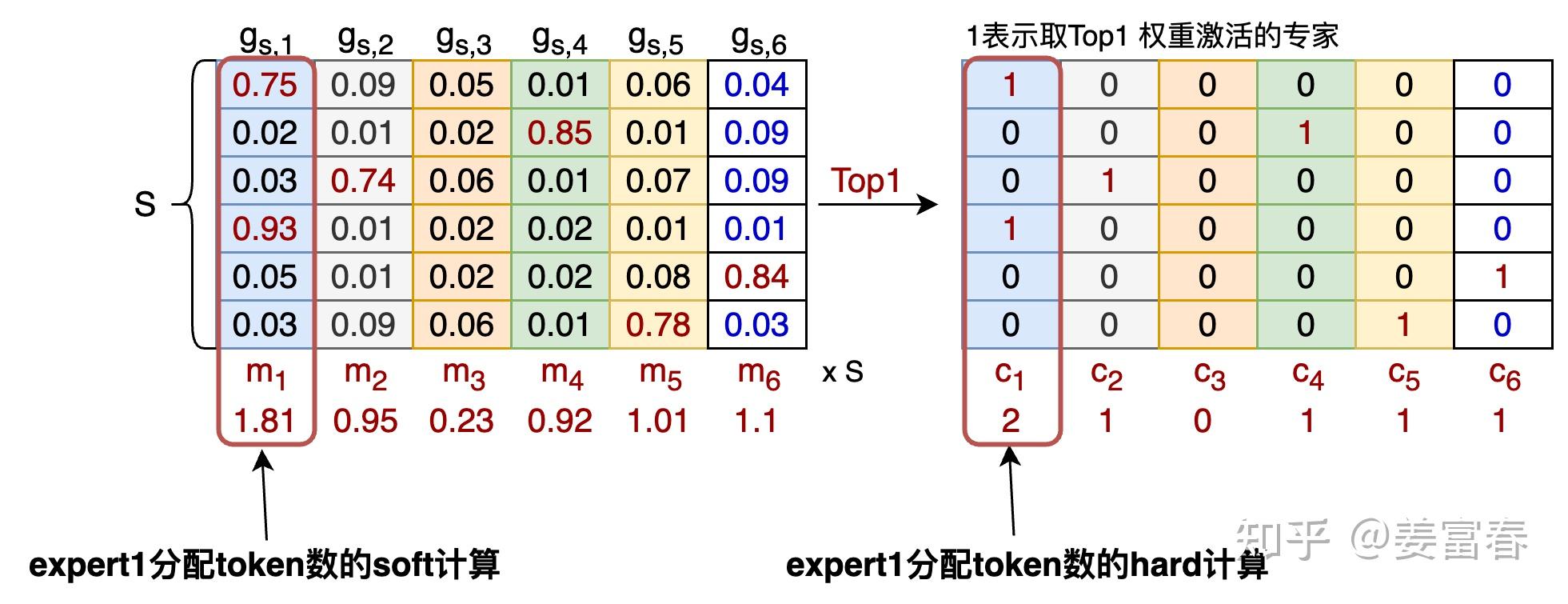
问题2:这样近似计算有什么好处?
答:因为
$$m_e$$
引入了 $$g_{s,e}$$
,而 $$g_{s,e}$$
由 $$softmax(w_g x_s)$$
得到,包含可学习参数 $$w_g$$
,因此整体可微,可用于梯度更新。
用
$$m_e$$
改造上面的平方项,常见的负载均衡损失形式为:
$$\mathcal{l}_{aux} = \frac{1} {E} \sum_{e=1}^E(\frac {c_{e}}{S}) \times m_{e}$$
这里也要注意:专家级负载均衡 loss 通常加到每个 MoE 层上,每层都有一个 $$l_{aux}$$
辅助损失。
有了基本背景,接下来进入 DeepSeek 在 MoE 方面的演进。
2. DeepSeek 的工作
2.1 DeepSeek-moe(V1)
2024 年 1 月 DeepSeek 发布 V1 版 MoE 模型,指出现有方法存在两方面问题:
- 知识混合性:现有 MoE 常用有限专家(如 8 或 16)。token 的知识丰富多样,将多样知识分配给有限专家,会让一个专家覆盖多类知识,变成“杂糅专家”,难以充分发挥专业效果。
- 知识冗余性:不同专家可能学到共同知识,导致多个专家参数学习到共享内容,出现冗余,进一步阻碍专家专业化。
为解决这些问题,DeepSeek 引入促进专家专业化的创新 MoE 架构,主要包含两方面优化:
- 细粒度专家分割(Fine-Grained Expert Segmentation):保持参数数量不变,通过分割 FFN 中间隐藏维度将专家切得更细。计算成本不变情况下,可激活更多细粒度专家,提高激活组合灵活性,让多样知识更细致地拆解到不同专家中,每个专家更“专”。
- 共享专家隔离(Shared Expert Isolation):隔离出部分专家作为始终激活的共享专家,捕获不同上下文中的共同知识。将共同知识压缩到共享专家中,减轻路由专家之间的冗余,提高参数效率,让路由专家更专注不同方面。
如下图2:(b) 在 (a) 基础上把隐层切得更细形成细粒度专家;(c) 在 (b) 基础上隔离共享专家。DeepSeekMoE 的演进一直延续这两个设置。
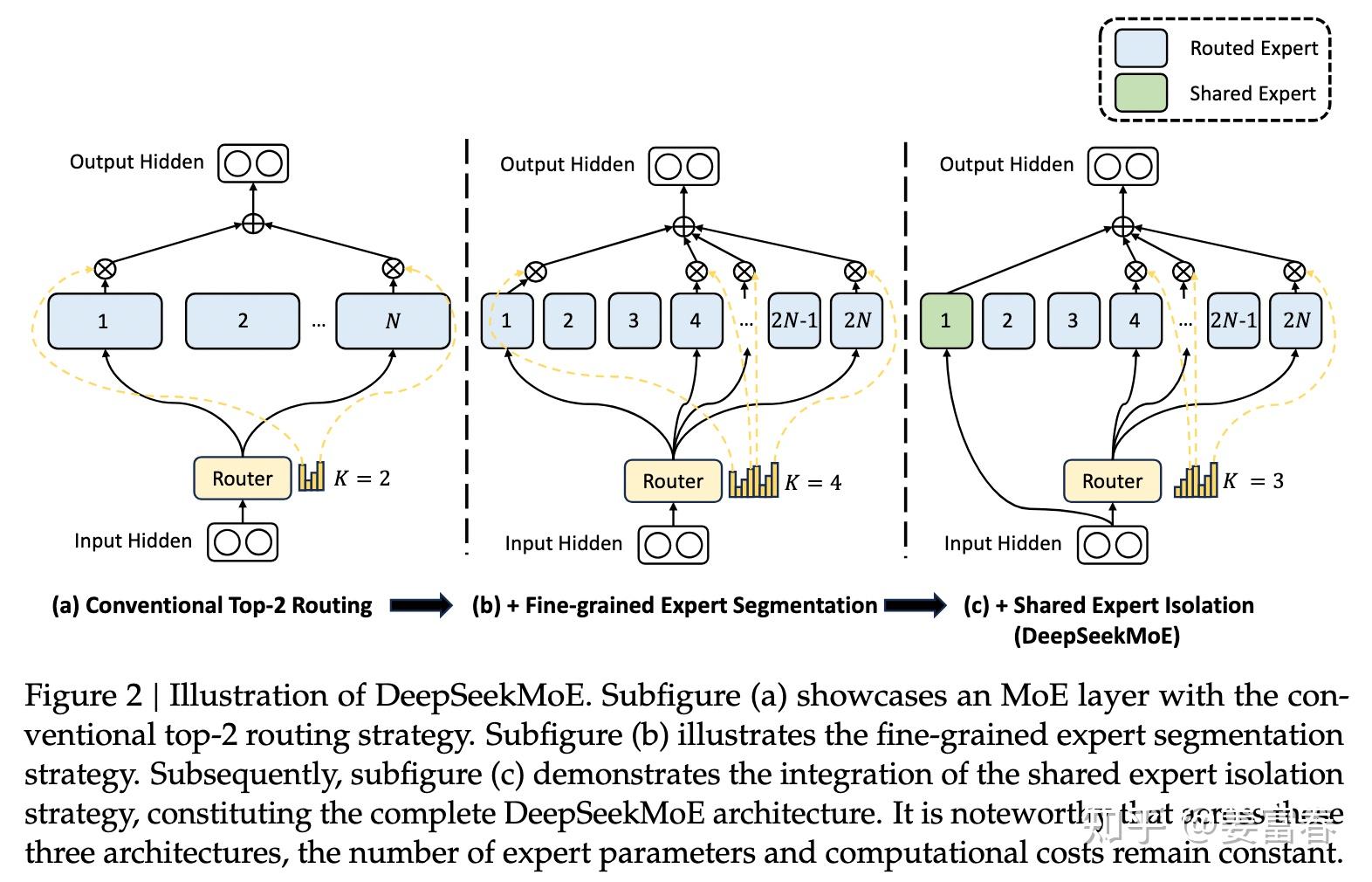
DeepSeekMoE 架构的公式形式如下:
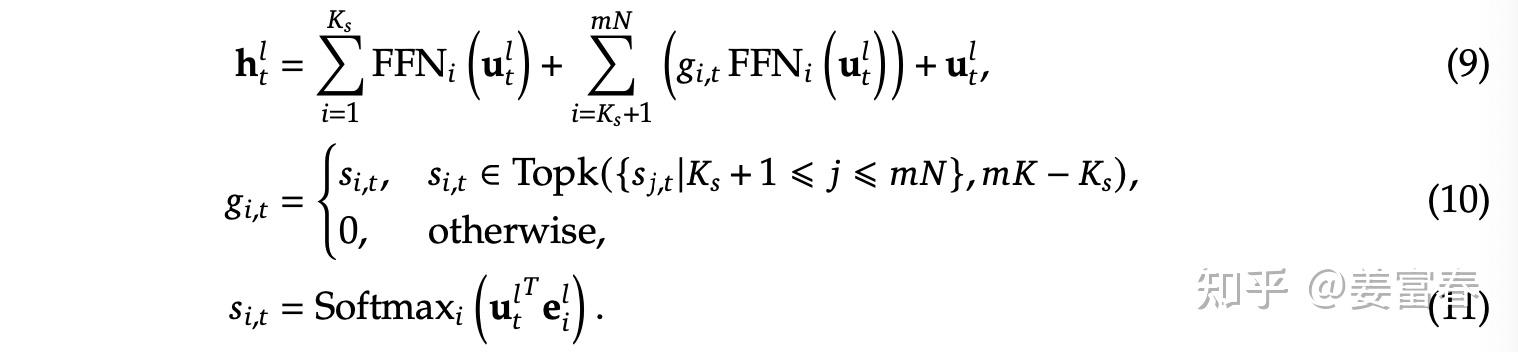
其中:
$$K_s$$
:共享专家数量$$mN - K_s$$
:路由专家数量$$u_t^l$$
:第 $$l$$
层第 $$t$$
个 token 的输入$$h_t^l$$
的三个因子:共享专家结果、路由专家结果、残差连接$$e_i^l$$
:第 $$l$$
层专家 $$i$$
的可学习参数$$s_{i,t}$$
:第 $$t$$
个 token 在专家 $$i$$
上的打分$$g_{i,t}$$
:取 TopK 高的专家权重
V1:负载均衡优化(两类 loss)
随着 DeepSeek 从 V1 到 V3 演进,负载均衡上做了很多工作。先看 V1 的负载均衡设置,主要包括两类:
1)专家级负载 loss(Expert-Level Balance Loss)
loss 计算如下:
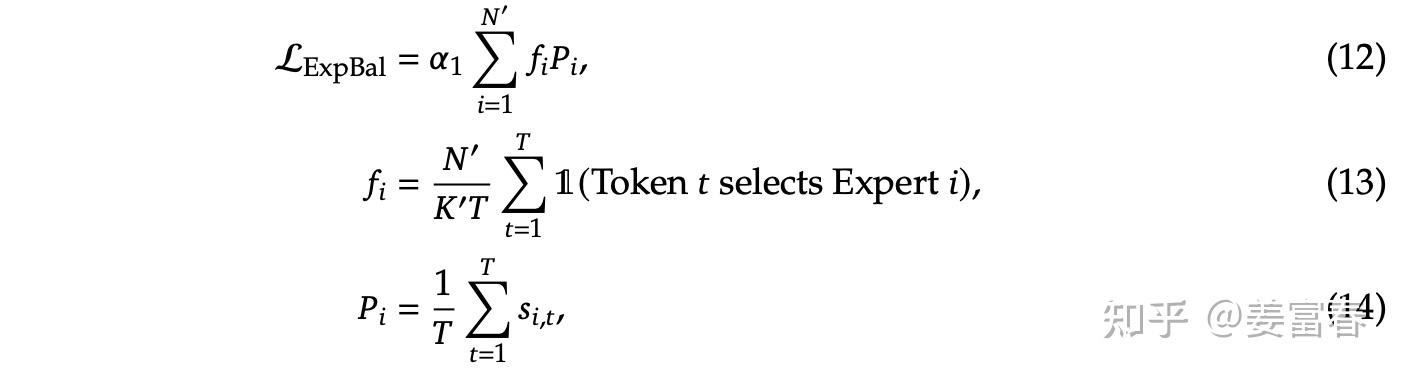
其中:
$$\alpha_1$$
:超参数,调节辅助 loss 相对主 loss 的权重$$T$$
:专家要处理的全部 token 数$$N' = mN - K_s$$
:去掉共享专家后的路由专家数$$K' = mK - K_s$$
:激活路由专家数$$\Bbb I$$
:指示函数
针对图4中
$$f_i$$
的计算,若参照第一节的形式,
$$f_i$$
可以写为:
$$f_i = \frac{1}{T}\sum _{t=1}^T\Bbb I(Token\quad t \quad selects \quad Expert \quad i)$$
但图4中的
$$f_i$$
相比上式,分子多乘路由专家数
$$N'$$
,分母多除激活路由专家数
$$K'$$
。
为什么要乘
$$N'$$
并除以
$$K'$$
?
核心原因:保持辅助 loss 的量级恒定,不随专家数量变化而变化。怎么理解?
- token 均匀分配时:
$$T$$
个 token,每个 token 激活 $$K'$$
个专家,总分配 token 次数为 $$TK'$$
,平均分给 $$N'$$
个专家,则每个专家分到 $$TK'/N'$$
。
- 于是按上面的定义有:
$$f_i = K'/N'$$
- 考虑
$$P_i$$
:token 均匀分配且 softmax 权重均匀落在激活专家上,权重大致为 $$1/K'$$
,则有:
$$P_i = \frac {1}{T} \times \frac{TK^{'}}{N^{'}} \times \frac {1} {K^{'}} = 1/N^{'}$$
- 因此 loss 中会出现随
$$K'/N'$$
变化的项。为了抵消这种动态项,整体乘以 $$N'/K'$$
,让 loss 量级不随专家数变化。
为什么要让 loss 量级不随专家数量变化?
1)超参
$$\alpha_1$$
更好调:太大影响主 loss 收敛,太小又达不到负载均衡目标。若辅助 loss 量级随专家数变动,调参会更复杂。
2)做专家数对比消融更可比:不同实验的 loss 绝对值更具参考意义。
2)设备级负载 loss(Device-Level Balance Loss)
将专家分为
$$D$$
组
$$\{\mathcal E_1, \mathcal E_2, ..., \mathcal E_D\}$$
,每组放在一个设备上。为了保证设备间的计算负载均衡,引入设备级负载 loss。该 loss 粒度更大,用于平衡不同设备的计算负载:
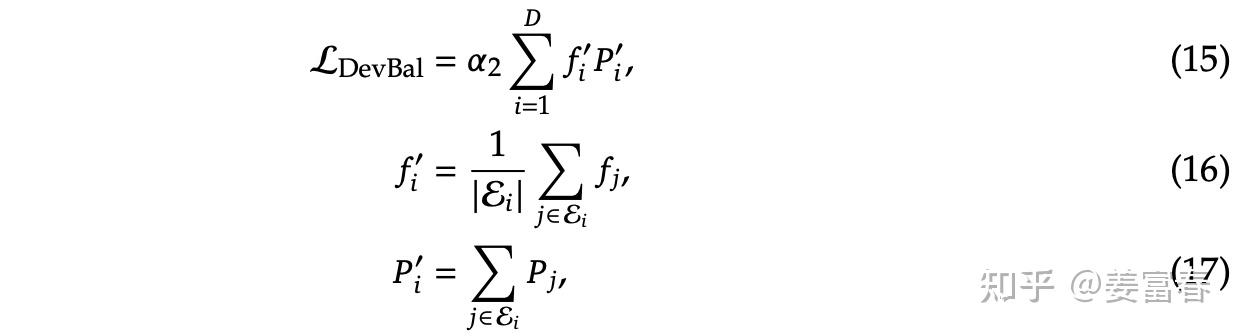
V1:一个容易忽略的问题——
$$T$$
的口径是什么?
公式中的
$$T$$
表示总 token 量。实际训练按 batch 输入,那
$$T$$
到底是全局累计、还是 batch 内即时?
看 V1 源码可知:以每个 batch 为一组 token 计算负载 loss,$$T$$
就是一个 batch 的总 token 量,并不跨 batch 累积。
源码链接: https://huggingface.co/deepseek-ai/deepseek-moe-16b-base/blob/main/modeling_deepseek.py#L361
核心代码如下(代码块内容保持不变):
class MoEGate(nn.Module):
def forward(self, hidden_states):
bsz, seq_len, h = hidden_states.shape
############################
# 这里的hidden_states就是公式里的T,是一个Batch数据的全部token做计算,每个Batch会重新计算
############################
hidden_states = hidden_states.view(-1, h)
logits = F.linear(hidden_states, self.weight, None)
scores_for_aux = logits.softmax(dim=-1)
topk_weight, topk_idx = torch.topk(scores_for_aux, k=self.top_k, dim=-1, sorted=False)
topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
ce = mask_ce.float().mean(0)
############################
# 计算Pi,fi 和 aux_loss。这里的计算并没有跨Batch累积,每个Batch单独计算
############################
Pi = scores_for_aux.mean(0)
fi = ce * self.n_routed_experts
aux_loss = (Pi * fi).sum() * self.alpha
2.2 DeepSeek V2:MoE 升级
DeepSeek V2 相对 V1,对 MoE 模块主要在负载均衡上做了三方面升级。
1)设备受限的专家路由机制(Device-Limited Routing)
随着 LLM 规模变大,MoE 训练通常采用专家并行(expert parallelism):一个 MoE 层的多个专家分配到多个设备并行训练。
DeepSeek 的 MoE 引入细粒度专家,专家数量通常很多(V2:路由专家 160 个,激活专家 6 个)。MoE 层多专家的输入相同,来自当前层 Self-Attention 的输出隐层激活值。若激活专家分布在多机,就需要把输入传输到多机,通信成本会放大。
为控制通信成本,V2 引入 设备受限的专家路由机制:保证每个 token 的激活专家最多分布到
$$M$$
个设备上(
$$M < TopK$$
)。做法分两步:
- 对每个 token,先选门控分数(图3公式11中的
$$s_{i,t}$$
)最高的专家所在的 $$M$$
个设备
- 将这
$$M$$
个设备上的所有专家作为备选集合,再从中选择 TopK 个专家
经验结果:当
$$M \ge 3$$
时,受限 TopK 与全局 TopK 的效果大致相当。因此 V2 配置为:TopK=6,M=3。
2)通信负载均衡 loss(Communication Balance Loss)
设备受限路由减少了“输入分发端”的多扇出通信量,但“接收端”仍可能出现 token 集中路由到少数设备,造成通信拥堵。因此 V2 在 V1 基础上增加通信负载均衡 loss:

其中:
$$\mathcal E_i$$
:第 $$i$$
个设备的一组专家$$D$$
:设备数$$M$$
:受限路由设备数$$T$$
:一个 batch 的 token 数$$a_3$$
:该辅助 loss 的超参
公式计算过程与专家级负载均衡类似。对
$$f_i^{''}$$
的计算乘以
$$D$$
并除以
$$M$$
,也是为了保持 loss 量级不随设备数或受限路由配置变化。
设备受限路由机制与通信负载均衡 loss 都是为了解决通信负载平衡:
- 前者在通信分发端设置上限;
- 后者在通信接收端鼓励平衡,促使每个设备接收等量 token。
两者结合,可以同时平衡设备输入与输出的通信负载。
3)设备级 Token 丢弃策略(Token-Dropping Strategy)
多个负载均衡 loss(专家/设备/通信)能引导平衡,但不能严格保证均衡。为进一步做计算负载均衡,引入设备级 Token 丢弃策略:
- 对一个 batch 输入 token,算出每个设备平均接收 token 量,即设备容量
$$C$$
- 对每个设备实际分配 token 量
$$T_d$$
,按路由打分(图3公式11的 $$s_{i,t}$$
)降序排列
- 若
$$T_d > C$$
,则将超过容量 $$C$$
的尾部 token 丢弃,不进行专家网络计算
注:丢弃 token 只是在单个 MoE 层不做专家计算,但该 token 仍通过残差传到上层 Transformer,继续参与计算。因此被丢弃 token 仍有 hidden_state 表征,只是表征来自“仅残差”,而不是“专家输出+残差”。并且不同层的 MoE 专家选择不耦合:某些层可能丢弃,另外层仍可参与专家计算。
为保持训练与推理一致性,训练阶段也保留 10% 样本不做 token 丢弃,以对齐推理阶段不丢弃的效果。
2.3 DeepSeek V3:MoE 升级
V3 在基本 MoE 框架上延续 细粒度专家(finer-grained experts) 与 共享专家(Shared Expert Isolation) 的设计,同时在门控网络与负载均衡方面做了改进。
1)门控计算:Softmax -> Sigmoid
V3 的 MoE 计算框架如图7:相对于前两版,主要将门控网络从 Softmax 升级为 Sigmoid。
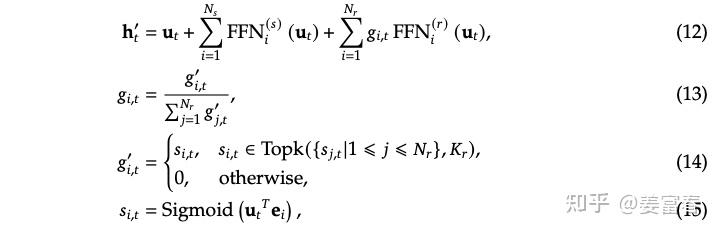
从“筛选 TopK”角度看,Softmax 与 Sigmoid 都能实现。但为什么要换?
对比专家设置变化:
- V2:路由专家数 160,激活专家数 6,总参数 67B,激活参数 21B
- V3:路由专家数 256,激活专家数 8,总参数 671B,激活参数 37B
这里一个直观解释是:路由专家维度变大时,Softmax 会对所有维度做归一化,维度越大,每个维度分到的值整体趋小;在选 TopK 时,会更依赖很小的小数位差异,区分度可能不足。Sigmoid 对每个专家独立输出
$$[0,1]$$
的打分,不随维度总数归一化,值域更“宽”,区分度更高,因此在更多路由专家的设置下更适配。
2)无辅助损失负载均衡(Auxiliary-Loss-Free Load Balancing)
V1/V2 通过专家级、设备级、通信级等辅助 loss 做负载均衡。但这些辅助 loss 主要服务计算/通信平衡,对模型效果调优不一定有帮助;一旦辅助 loss 太多或量级太大,还可能干扰主模型优化。
因此 V3 将多类辅助负载 loss 精简掉,通过引入可动态调节的 bias 来做负载均衡。
- V2 选择专家:依据门控权重
$$s_{i,t}$$
取 TopK
- V3 为每个专家维护一个可动态调节的 bias
$$b_i$$
,选择 TopK 基于:
$$s_{i,t} + b_i$$
当检测到专家过载时,减小该专家的
$$b_i$$
,降低路由到该专家的 token;当检测到负载不足时,增大
$$b_i$$
,提升被选概率。
论文里这部分描述较含糊:如何检测过载/不足?是否用专家平均 token 数?作者也尝试看 V3 源码( https://huggingface.co/deepseek-ai/DeepSeek-V3-Base/blob/main/modeling_deepseek.py ),但未找到明确实现细节,只看到
$$b_i$$
似乎设置成可学习参数,这与论文“增加/减少固定 $$\lambda$$
”的描述也不完全一致。可能是实现位置没找到,后续还需补充信息再对齐细节。
3)sequence 粒度的负均衡损失(Complementary Sequence-Wise Auxiliary Loss)
V3 增加了 sequence 粒度的负载均衡损失,用来平衡单个 sequence 的 token 在专家间的分配,如图8:
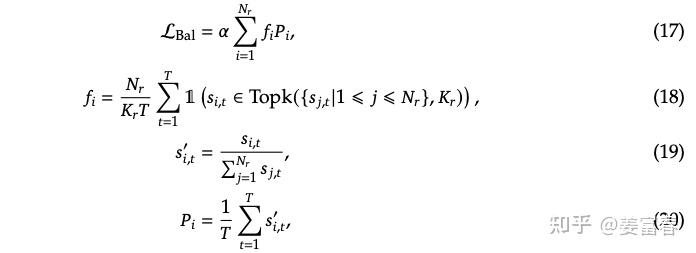
与 V1 的 Expert-Level Balance Loss 的主要区别是作用粒度:
- Sequence-Wise:单条样本(单 sequence)粒度做计算
- Expert-Level:一个 batch 的多 sequence token 共同做计算
计算形式本身差异不大。
V3 也强调:通过上述负载均衡策略能达到很好的平衡效果,因此 V3 并没有 token 被 drop 掉。
3. 总结
回顾 DeepSeek 在 MoE 方面的创新与演进:
- V1:为兼顾通用知识与细粒度领域知识建模,引入 共享专家(Shared Expert) 与 细粒度专家(Fine-Grained Expert)。为平衡计算负载,引入 专家级负载 loss(Expert-Level Balance Loss) 与 设备级负载 loss(Device-Level Balance Loss)。
- V2:重点优化通信负载,引入 设备受限的专家路由机制 与 通信负载均衡 loss,确保设备输入/输出通信负载更均衡。
- V3:考虑多辅助负载 loss 可能干扰主模型,精简辅助 loss,通过在门控权重上增加可调 bias 解决通信与计算负载;引入更细粒度的 sequence 负载均衡 loss。同时在路由专家增至 256 的情况下,为增强区分度,用 Sigmoid 替换 Softmax 作为门控函数。
整体演进过程如下图所示:

4. 参考文献
- Adaptive Mixtures of Local Experts: https://ieeexplore.ieee.org/abstract/document/6797059
- GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding: https://arxiv.org/pdf/2006.16668
- DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models: https://arxiv.org/pdf/2401.06066
- DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model: https://arxiv.org/pdf/2405.04434
- DeepSeek-V3 Technical Report: https://arxiv.org/pdf/2412.19437