RNN解析：如何赋予神经网络记忆能力以处理序列数据？

在全连接神经网络（FNN）展现了其普适性，卷积神经网络（CNN）证明了其在空间维度上的强大之后，我们今天来探讨循环神经网络（RNN）。RNN旨在解决的根本问题，正是序列与时间，而其实现方式，则是为网络注入“记忆”。

尽管在当今的自然语言处理等领域，Transformer架构已成为绝对主流，但RNN作为序列建模的奠基者，首次系统地让神经网络具备了处理先后顺序的能力。理解RNN，是理解机器如何“记忆”的关键一步。

FNN与CNN的“失忆症”

在RNN出现之前，无论是FNN还是CNN，在面对序列数据（如文本、语音或金融时间序列）时都有一个共同的短板：它们缺乏时间维度的概念，每一次的输入都被视为相互独立的事件。

举个例子，有这样一句话：“我肚子饿了，我想去__。”

要准确预测空白处应填“吃饭”，模型必须理解前文“肚子饿了”所提供的信息。然而，在传统的FNN看来，每个输入是孤立的。当它处理“我想去”这几个字时，并不会（也无法）考虑之前输入的“我肚子饿了”所建立的语境，它只是将这些词视为并列的特征。

对于擅长处理空间信息的CNN也是如此。它能识别一张静态图片中的猫，却无法理解一段视频中，猫在上一秒跳跃后，下一秒将落在何处。它们都患上了“时间失忆症”。

RNN：为网络装上“记忆单元”

人类在阅读时，并非孤立地识别每一个字。我们的大脑会将上文信息暂存于工作记忆中，并随着阅读的推进不断更新这份记忆，从而理解完整的上下文。

RNN的设计灵感正源于此，其核心思想直观而深刻：当前时刻的输出，不仅取决于当前的输入，还依赖于过去所有时刻的“记忆”摘要。

这一设计通过两个关键机制实现：隐藏状态与参数共享。

（1）隐藏状态：RNN的“记忆便签”
隐藏状态是RNN的“记忆条”。在每个时间步，网络都会接收当前的输入，并结合上一时刻的隐藏状态，计算并输出一个新的隐藏状态，传递给下一时刻。这有效地打破了时间步之间的隔阂。

你可以将其想象成一个“传话游戏”。游戏中的每个人（即每个时间步的RNN单元）都有两样东西：

• 新线索：当前时刻从外界获得的信息（输入向量 X_t）。
• 旧便签：上一个人传递过来的纸条（上一时刻的隐藏状态 H_{t-1}）。

这个人需要将“新线索”和“旧便签”结合起来，经过处理（应用权重和激活函数），写出一张“新便签”（当前隐藏状态 H_t），然后传给下一个人。这张不断传递的“便签”，就是对截至当前时刻所有历史信息的一种精炼和压缩表示。

（2）参数共享：时间维度的“以不变应万变”
与CNN在空间维度上共享卷积核类似，RNN在时间维度上共享同一套权重参数。无论序列有多长，处理每个时间步的逻辑都是一样的。这极大地减少了模型参数量，并使其能够泛化到训练中未见过的序列长度。

RNN的循环：时间维度上的展开

RNN的结构看似一条由相同单元首尾相连而成的链，但实际上它只有一个神经网络单元，在时间维度上被重复使用。这种极简的设计是参数共享的直观体现。

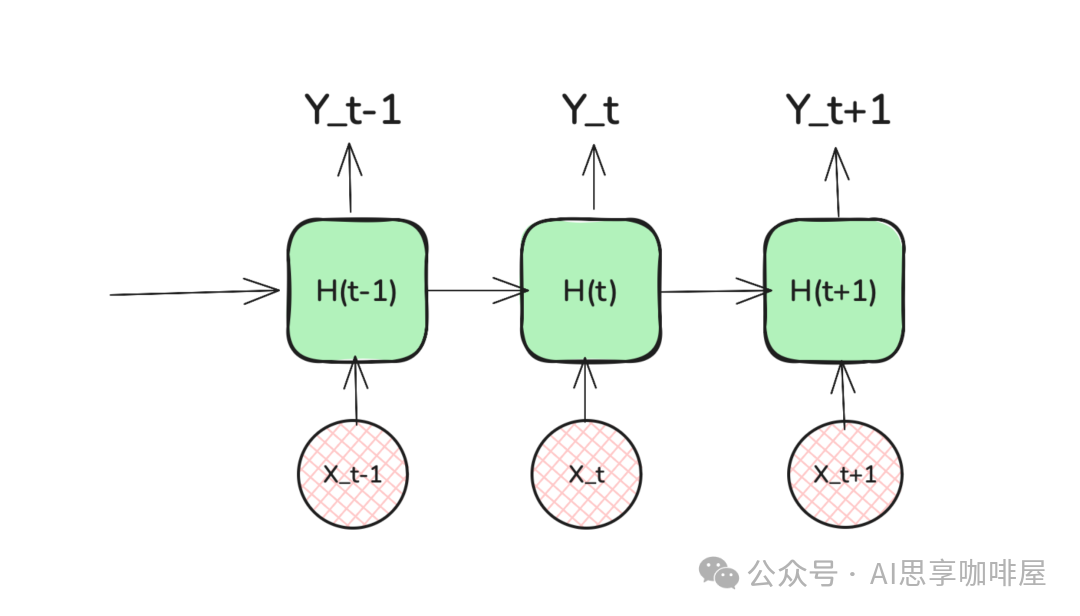
在FNN中，若要处理一个10个词的句子，可能需要为每个词位配置独立的参数。而在循环神经网络（RNN）中，无论句子是10个词还是100个词，负责处理“传话”规则的都只有那一个单元。这种设计让模型学会的是语言或序列中普遍的规律，而非死记硬背特定位置的内容。

此前我们学习Transformer时了解到，其注意力机制本身并不内含顺序信息，需要依靠位置编码来显式注入。而RNN则通过计算的先后顺序隐式地编码了位置信息——位置是内置于其串行计算路径之中的。两者都重视次序，但实现哲学不同：RNN依靠结构，Transformer依靠输入增强。

RNN的局限：记忆虽好，但容量有限

尽管RNN在理论上可以处理任意长度的序列，但在实际应用中，它面临着两大显著挑战。

1. 梯度消失：长程记忆的稀释
这是RNN最著名的痛点。当序列非常长时（例如超过100个时间步），早期时间步的信息在向后传递的过程中会逐渐衰减，直至消失。这就像传话游戏进行到第100个人时，最初的信息早已面目全非。在数学上，这表现为反向传播时，梯度因连续相乘而指数级缩小（梯度消失），导致模型无法有效学习远距离的依赖关系。

2. 无法并行：串行计算的代价
RNN的计算本质上是严格串行的。你必须先计算出 h_1，才能计算 h_2，然后再计算 h_3……这种依赖性使其无法充分利用现代GPU强大的并行计算能力，导致训练速度较慢。

正是由于这些局限性，后续的改进模型如LSTM和GRU通过引入“门控机制”（一种选择性地记忆和遗忘信息的结构）来缓解长程依赖问题。而Transformer架构则通过自注意力机制彻底抛弃了循环结构，实现了完全的并行计算，从而在大多数序列任务上取代了RNN。

然而，纵观整个发展历程，RNN是理解序列建模思想的基石。如果说CNN是机器认知世界的“眼睛”，那么RNN就是机器尝试拥有“记忆”的第一次系统性探索。站在今天的视角看，没有RNN在序列建模上的奠基性工作，或许就不会有后来Transformer的横空出世，以及我们所处的大模型时代。

学习RNN时，深入思考以下问题能帮助我们更好地理解其本质与局限：

1. RNN的参数量具体如何计算？与FNN、CNN相比有何特点？
2. RNN理论上能处理变长输入，而FNN输入固定，Transformer的输入长度限制又是怎样的？
3. LSTM和GRU中的“门控机制”具体是什么？它们如何解决RNN的长程遗忘问题？
4. 既然RNN参数共享，为什么h_t的计算必须串行？理论上能否推导出并行计算方法？

这篇概述帮助我们建立了对RNN的初步认知。在后续的深入学习中，我们将会逐一探讨这些问题的答案。对深度学习序列模型感兴趣的开发者，欢迎在云栈社区的“人工智能”板块交流探讨，共同拆解更多模型细节与实践案例。