深入解析Sparse Attention：从O(N²)复杂度瓶颈到内在稀疏结构与优化实践

TL;DR

去年8月，我曾整理分析了一篇论文《大模型时代的数学基础(9)- SDPA和最优传输, 强化学习及信息几何的联系》。最近发现作者在去年十月写了一篇博客 《Your Transformer is Secretly an EOT Solver》，详细阐述了这篇论文背后的一些故事，以及对寻找线性注意力机制算法的一些探索。

作者通过一个引人入胜的叙事，从尝试构建一个亚二次方复杂度注意力的失败经历，引出标准的缩放点积注意力机制在数学上等价于一个特定形式的单边熵优化输运问题的精确解这个数学发现。今天就来展开读一读这篇。

大概的背景

文章开篇作者谈到：

九个月前，还是十个月前？我已经学会在深陷问题时不再相信自己的时间感。任何面临重大截止日期或长时间被某个特定问题困扰的人都会直观地理解，时间在那时变成了别的东西。它不再是小时的有序递进，而是一种黏稠的介质，人在其中移动越来越困难，就像一个离岸太远的游泳者，发现海水变得黏稠而充满阻力。我当时在做我见过别人做过的事，或者说，我一直以来都在做但没有完全承认的事：试图发明又一个亚二次方复杂度的注意力机制。是的，又一个。仿佛这个世界还需要更多这种东西似的。

标准的自注意力机制的计算复杂度和内存复杂度都是 O(N²)，其中 N 是序列长度。这是因为需要计算序列中每对 token 之间的注意力得分，形成一个 N x N 的注意力矩阵。当 N 很大时，在处理长文档、Agent任务以及多模态中高清图像或长视频时，O(N²) 的开销变得难以承受。

“亚二次方注意力”指的是任何复杂度低于 O(N²) 的注意力变体，例如线性注意力 O(N)，对数注意力 O(N log N) 等。多年来，学术界提出了大量的此类方法，如 Linformer， Reformer， Performer， Sinkhorn Attention 等。作者的自嘲正是对这一研究领域“内卷”现象的调侃。

然后作者开始尝试：

但我的方案，当然，将会与众不同。我的方案将是新颖而奇特的。我的方案将反映实际的考量；真实的常数和实现细节，而不仅仅是纯粹的大-O 算法晦涩主义。
这个想法，大致上，涉及一种近似。但并非任何近似。这是一种随着序列长度 N 增长而渐近精确的近似。也就是说：它在所有不重要的方式上是错的，却在唯一重要的方式上是正确的。当然，出现了一些意料之外的问题。这个领域总是存在一些意料之外的问题，这几乎是一条定理。

这个意料之外的问题就是：任何亚二次方注意力机制在数学上都不可能在所有输入上实现渐近精确。

为何渐近精确的亚二次方注意力是不可能的

作者从大海捞针的构造谈起，构造了一个不可能假设。

其直觉来自于一个 “大海捞针” 的构造。Softmax 函数需要知道每一行中所有的查询-键相似度才能正确计算归一化常数。如果一个算法只检查了 o(N²) 个查询-键对，那么根据鸽巢原理，必定存在至少一个查询行 i，算法对该行只检查了 o(N) 个键。在一个未被检查的位置放置一个任意大的相似度得分，即 “针”，算法就会灾难性地失败，因为它缺少了计算注意力权重所必需的信息。

更形式化地，定义一个亚二次方算法为计算 o(N²) 个 QK 点积的算法，定义渐近精确为当 N -> ∞ 时，其输出收敛于精确的注意力矩阵。假设，为了引出矛盾，存在这样一个算法 A。

由于亚二次方性，每个查询平均检查的键的数量是 o(N)。因此，存在一个查询索引 i 和一个对应的未被检查的键索引 j。现在构造一个对抗性输入：令 q_i = u，令 k_j = v，其中 u^T v = M，并将所有其他的查询，键和值向量都设为零向量。对于行 i，精确的注意力输出几乎完全集中在位置 j 上，当 M -> ∞ 时收敛于 e_j。但是，由于算法 A 从未检查过 (i， j) 位置，它没有关于这个主导性贡献的任何信息，因此必须输出近似为零的结果，从而在极限情况下产生一个无法消失的误差下界 |e_j - 0|_1 = 2。

这个矛盾源于 Softmax 内在的全局归一化特性：计算精确的注意力权重需要关于每一行中所有Query-Key相似度的完整信息。一个亚二次方算法无法同时为所有行提供这种完整信息，使得渐近精确变得不可能。

注意力作为熵优化输运

作者关于 SDPA 从 EOT 的视角来分析是很有新意的一个视角。

首先构建这个优化输运问题。考虑为一组 N_q 个查询向量计算注意力权重的标准设置，这些查询向量逐行收集到一个大小为 N_q x d 的实矩阵 Q 中。

这些查询关注于一组 N_k 个键向量，它们逐行收集到一个大小为 N_k x d 的实矩阵 K 中。

我们的目标是构建一个优化输运问题，其唯一解恰好是注意力权重矩阵 P，其中每个元素 P_{ij} 由带有温度 τ 的缩放点积注意力定义：

P_{ij} = softmax(q_i^T k_j / τ)_j = exp(q_i^T k_j / τ) / Σ_{l=1}^{N_k} exp(q_i^T k_l / τ)

矩阵 P 的每一行之和为1，所以 P 是一个行随机矩阵。

Query源空间和测度

源索引集是 I = {1， …, N_q}，每个索引对应一个查询向量。源测度 α 为每个源索引分配单位质量。换句话说，对所有 i ∈ I， α_i = 1，所以总源质量为 N_q。你可以认为每个查询 q_i 发出一个单位的注意力质量，等待被分配到各个目标索引上。

Key目标空间

目标索引集是 J = {1， …， N_k}，每个索引对应一个键向量。每个 j ∈ J 是一个潜在的目的地，可以接收来自任何源 i ∈ I 的质量。

一个关键的选择是如何处理目标集上的目标边缘分布 β。与同时固定源和目标边缘分布的经典优化输运不同，我们让目标边缘分布是自由的。到达目标的质量分布没有被预先约束，将由优化过程决定。这是一个单边优化输运问题。

作者在这里完成了最关键的一步：将注意力机制精确地表述为一个 EOT 问题。

1. 优化输运的基本要素：

   • 源分布 α：在这里是 N_q 个离散点，每个点的“质量”是 1。这对应于注意力机制中，每个 query position 的注意力权重之和必须为 1。
   • 目标分布 β：在这里是 N_k 个离散点。
   • 成本矩阵 C：从源 i 输运单位质量到目标 j 的成本。作者巧妙地定义为 C_{ij} = -q_i^T k_j，将注意力中“最大化相似度”的目标转化为 OT 中“最小化成本”的目标。
   • 输运计划 P：一个 N_q x Nk 的矩阵，P{ij} 表示从源 i 输运到目标 j 的质量。

2. 关键设定：单边约束和熵正则化：

   • 单边约束：经典的 OT 要求输运计划 P 的行和等于源分布，列和等于目标分布。文中的“单边”表明没有目标边缘约束这一事实，即作者只约束了行和，而目标分布是自由的。这契合了 Attention 的特性：每个 query token 自行决定如何分配其注意力，而 key token 只是被动地接收，并没有对自身接收的总注意力有任何限制。
   • 熵正则化：熵正则化最优输运是在经典最优输运问题的目标函数中加入一个熵正则化项，从而在计算上获得巨大优势。首先是可以通过 Sinkhorn 算法快速求解；其次具有可微性，其解是严格凸的，可以无缝集成到神经网络训练中；最后，它自然地提供了一种“平滑”的对应关系，在某些应用中比严格的一对一映射更有意义。

证明

在前面的文章《大模型时代的数学基础(9)- SDPA和最优传输, 强化学习及信息几何的联系》中已经详细进行了分析，在此略去。

一些展望

这是我最近一直在思考的问题。我比较同意作者的观点，从计算的复杂度上来看我们似乎过分地执着于 O(N²)。事实上从底层来看我们似乎必须 O(N²) 地去扫描一遍 QK。但是从模型深度的维度来看，中间某些层交替地使用一些线性注意力机制，保证某个比例的 Full:Linear 似乎也说得过去，这样也能达到降低计算复杂度的目的？

从 Attention 的内在代数结构上来看，它本质上是稀疏的。正如我在《谈谈DeepSeek mHC》中介绍的一个话题：

DeepMind的Demis Hassabis眼中的大千世界：世界存在某种结构压缩的低维流形。

事实上我们在试图寻找一种算法，识别出这些结构，就能实现压缩、调度与迁移，从而在无序中建立智能与控制。

这些便是 Attention 的实质。假设它是一个层次化的交错结构。例如下图：

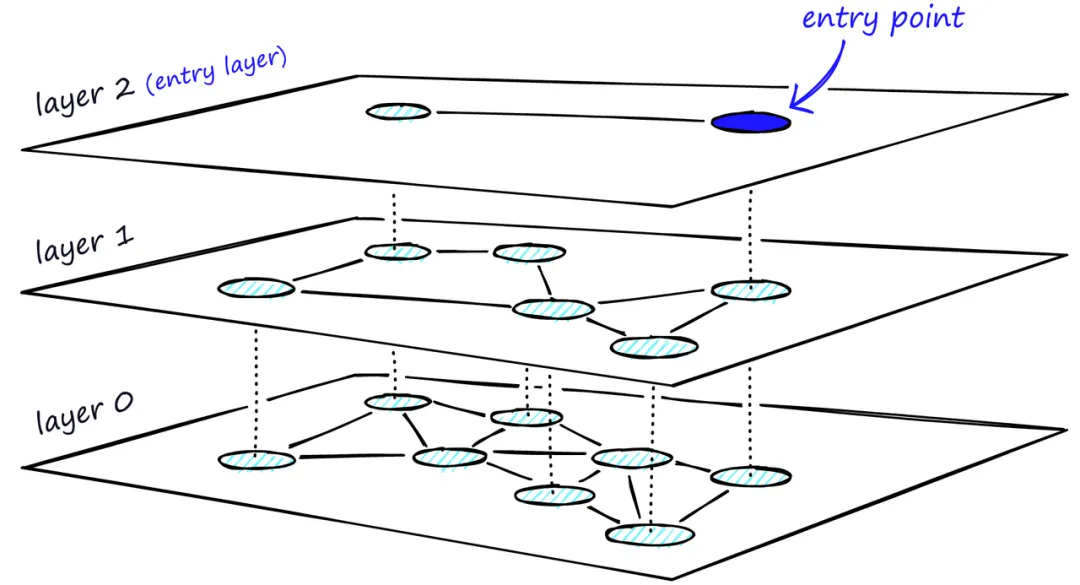
通常我们会有一些常见的算法去处理。

由底而上的“筛”法

这涉及到一个 Nerve 构造的结构，从词语到短语，再到句子，段落，章节等等……从这个角度做一些“筛选”，实质上和 DeepSeek 的 Engram 做法就有些类似了，详细的内容可以参考《谈谈DeepSeek Engram: Conditional Memory》中的第九章的内容。并且筛选的结果某种意义上通过 mHC 传递到了模型的后续若干层中。

自顶而下的“鸟瞰”法

另一方面是，既然知道底层是稀疏的，那么是否可以就像我们查看一个地图那样，先用一个相对偏小的算力去模糊化地“鸟瞰”整个“地图”，然后逐渐地放大去查看局部的细节。这里就类似于 DeepSeek 的 DSA了，在《学习一下DeepSeek-V3.2》中有详细的阐述。通过构造一个 Lighting Indexer 来选择需要计算的 Token。

虽然当前的 DSA 有一个 hardcode 的 topk=2048，但我估计如果像 DeepSeek-V4 这样重新训练的模型，可能还有一些 Dynamic Topk 的机制。

两者的结合

DeepSeek 在某些层插入 Engram 的方式将 N-gram 的信息注入后，某种意义上来说是在模型的中间若干层强化了这些 N-gram 构成的单纯形的注意力分数。使得后续若干层 Attention 的算力更多的花费在单纯形之间的注意力分数计算。然后和 DSA 一起结合起来，从而达到“从上而下”和“由底而上”的组合。

也就是说既承诺了在整个模型中进行了 O(N²) 的扫描，但是算力进行了节省。也就是这篇作者谈到的一个观点：O(N²) 如果不能避免，那么去削减它的常数项来达到节省算力的目的。

当然另一方面肯定要对比 Full 和 Linear 混合类的模型，例如 Qwen GDN / Kimi KDA 一类的模型，似乎从 Linear Attention 的 RNN 构造来看，它也是一个类似的由底而上的“卷”法，将 Attention 卷到一个状态矩阵中，并不停地用 KV 来更新和压缩。使得 Q 到 K 的 EOT 问题降低到一个更小的规模。

两者之间的对比，特别是推理阶段则要从 KVCache 的处理难度上进行一些分析，具体的内容还需要看两种做法对 KVCache 的算法优化程度。

另一方面是对 O(N²) 的常数项进行比较。例如 Linear Attention 通常采用 3:1 的比例下，常数项相对于 Full Attention 粗略估计为 1/4，那么对于 DSA 这类 Sparse Attention，只要我们处理 Lightning-Indexer 的复杂度小于 3/4 O(N²) 即可赚回来，因为后续的全尺度的稀疏 Attention 是在挑选出来的 topk 个 token 中进行计算的，可以视为一个常数 O(k²) 复杂度的运算。

从算法层面上来看，个人觉得像 DeepSeek 这样 Sparse Attention + Engram + mHC 的处理方式更为优雅一些。那么接下来其实还有个探索的路径就是 DSA + Linear Attn 的比较。这个等哪家做出来再分析吧，但是我怀疑的是 Linear Attn 层中的 State 经过过度的压缩是否能够达到一个较好的模型效果？

参考资料
[1] Your Transformer is Secretly an EOT Solver: https://elonlit.com/scrivings/your-transformer-is-secretly-an-eot-solver/