支持向量机解析：如何用数学与核技巧实现高维空间最优分类？

在机器学习的发展历程中，有一个算法因其严谨优雅而被誉为“经典之作”：它不像深度学习那样依赖海量参数，也不像简单线性模型那样能力有限，却在众多分类任务中表现卓越，这便是支持向量机（Support Vector Machine，SVM）。

许多初学者初次接触这个名字时，都会感到疑惑：这个名称听起来有些抽象，它究竟在“支持”什么呢？

01 缘起：如何优雅地画出分界线？

要理解 SVM，我们不妨先放下复杂的数学公式，从一个最直观的日常场景开始。

假设你面前的桌子上散落着两种积木：红色圆形和蓝色方形。你的任务是在桌上画一条直线，将这两种积木完全分开。

这就是机器学习中最基础的 “二分类问题”。

1、无数种可能

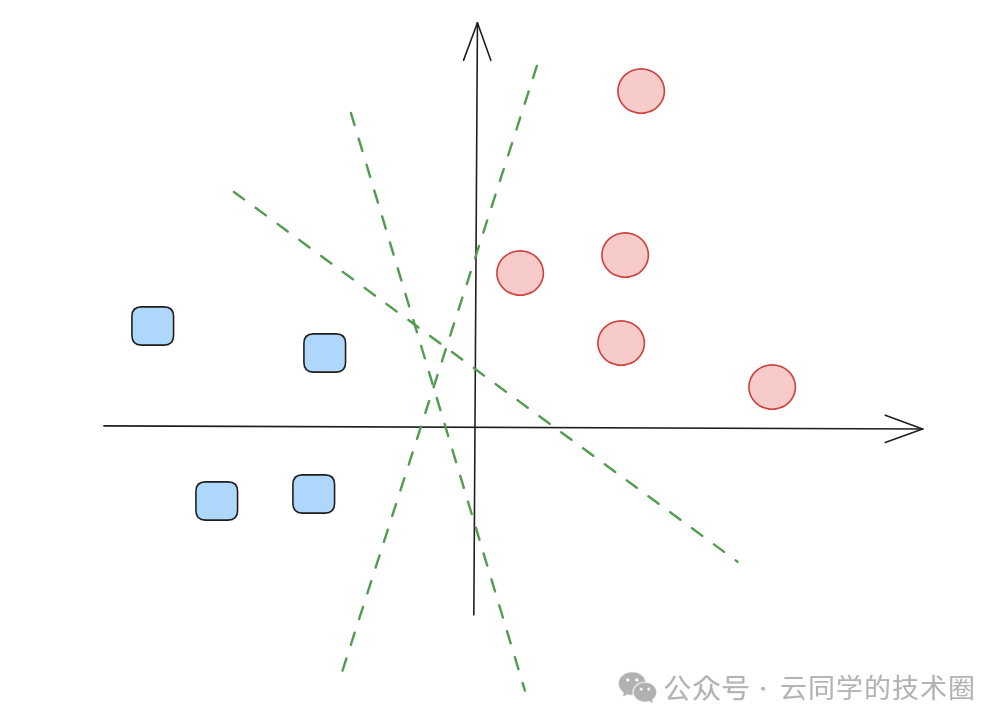
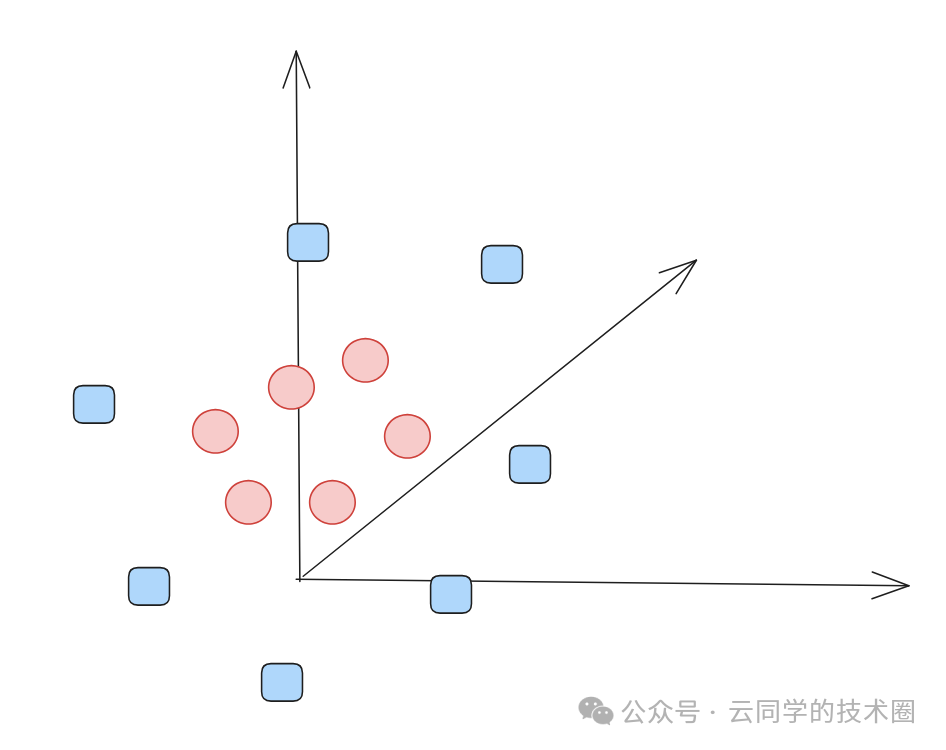
如上图所示，对于这样一组点，我们能画出无数条直线将它们分开。从数学上讲，在二维空间中，能将两类点正确划分的直线（在高维空间称为超平面）确实有无数条。

2、哪一条才是“最好的”？

我们熟知的感知器模型，其目标仅仅是找到任意一条能分开的线。但 SVM 不同，它是一个“完美主义者”。SVM 认为，仅仅分开是不够的，我们需要这条线离两边的积木越远越好。

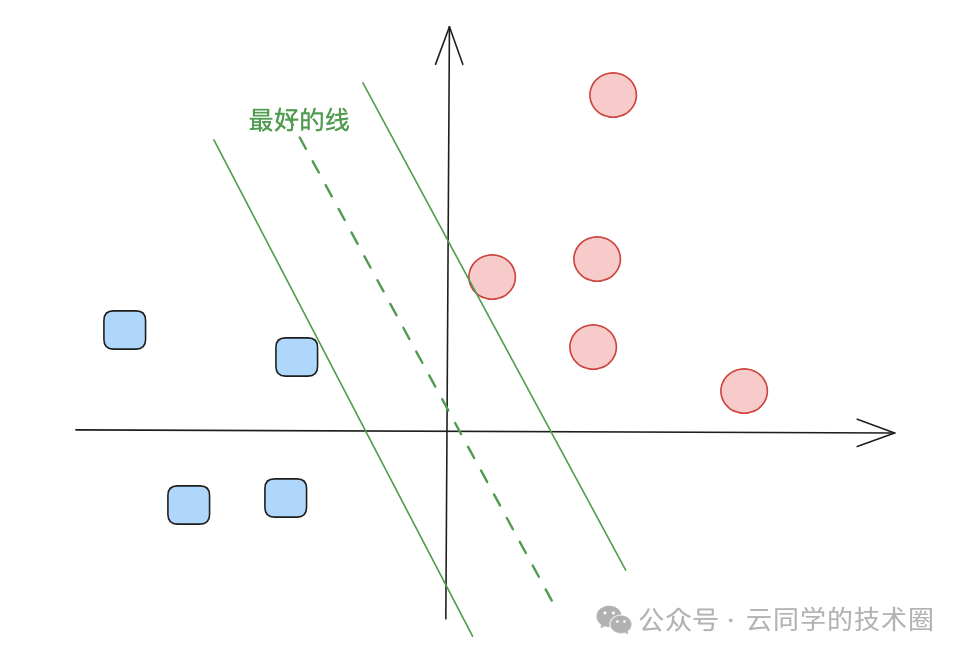
图中间的虚线，正是那条离两侧数据点最远的“最佳分界线”。

为什么间隔越大越好？ 原因很朴素：

• 抗噪能力更强：如果分类边界紧贴着样本，数据稍有扰动或噪声就可能导致误判。更大的间隔为分类决策提供了“安全缓冲区”，提升了模型的稳定性。
• 泛化能力更好：机器学习的核心目标不是完美拟合训练数据，而是在未知的新数据上表现良好。一个拥有最大间隔的决策边界，意味着模型对新样本的包容性更强，泛化能力更优。
• 几何解释清晰：SVM 从纯粹的几何角度出发，将分类问题转化为寻找一个最“安全”、最“宽阔”的分界平面，目标明确且直观。

02 “支持向量”到底在支持什么？

最大间隔，是支持向量机的核心思想。随之而来的问题是：这条最好的边界，究竟由谁决定？

1、谁才是真正的“关键少数”？

在一个包含百万样本的数据集中，是否每个样本都对最终分类器有同等贡献？在逻辑回归或神经网络中，答案是肯定的，所有样本都通过损失函数影响模型参数的更新。

但在 SVM 中，答案截然不同。

当找到那个“最大间隔”分界线后，你会发现：绝大多数样本点都安稳地呆在远离边界的安全区内。真正决定这条边界位置的，只有少数几个点——它们恰好位于间隔的边缘，就像两军对垒时最前线的“哨兵”。

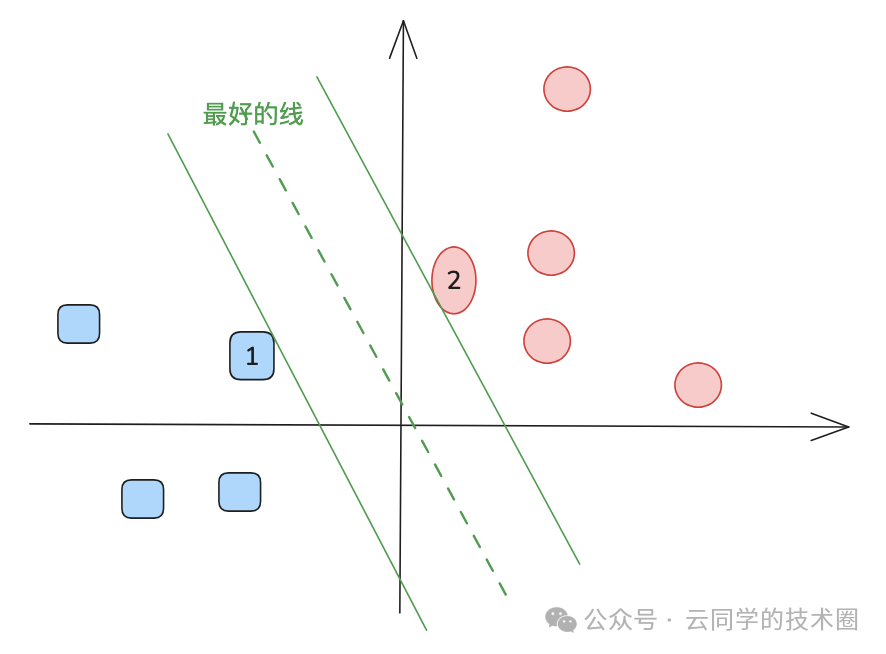
上图中标号为1的蓝色方块和标号为2的红色圆圈，就是这样的“前线哨兵”。它们的位置直接决定了分界线的走向，而其他所有的积木（样本点）对边界位置没有任何影响。

这些处于间隔边界上的关键样本点，被称为“支持向量（Support Vectors）”。

• “支持”的含义：正是这些点“支撑”起了整个分类器的边界框架。移除非支持向量，边界岿然不动；但移动任何一个支持向量，边界必将随之改变。
• “向量”的含义：在数学上，每一个样本点都可以视为特征空间中的一个向量。

因此，SVM 体现了一种 “精简的哲学”：决定事物本质区别的，往往不是沉默的大多数，而是那些处于极限和边界情况的个体。

2、超平面：不仅仅是一条线

在二维平面，分界线是一条直线；在三维空间，它是一个平面。当维度上升到 N 维时，这个分界实体被称为 超平面（Hyperplane）。

SVM 的核心任务，就是在 N 维特征空间中，找到一个能够正确分割两类数据，且令所有支持向量到该超平面距离（即“间隔”）最大的超平面。

03 当世界不再是“非黑即白”

以上讨论的是理想情况。现实世界的数据往往错综复杂，无法用一条直线简单分开。如下图所示，当数据呈现同心圆分布时，任何直线都无法将其完美分割。

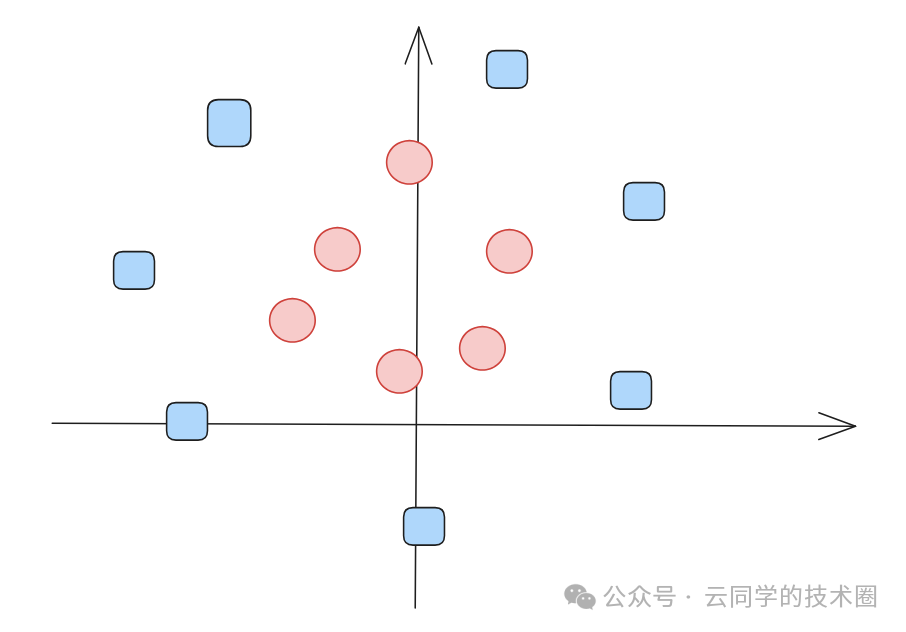
为此，SVM 引入了两大“神器”：核技巧（Kernel Trick） 与 软间隔（Soft Margin）。

1、升维打击：核技巧

这是 SVM 最具魅力的一点。如果在原始特征空间里数据线性不可分，那就将它们映射到一个更高维的空间中去。

可以这样想象：当桌子上的红蓝积木混杂一团无法用线分开时，我们猛地一拍桌子，所有积木弹起到空中（进入三维空间）。在三维空间里，我们就能轻松地用一个平面（如一张纸）从中间将两种颜色的积木隔开。

核函数的魔力就在于实现这种高维映射。最精妙的是，通过数学上的技巧（如核函数定理），我们无需真正计算每个样本在高维空间中的具体坐标，而只需计算它们在高维空间中的内积。这种“迂回战术”让 SVM 能够高效地处理极其复杂的非线性分类问题，而计算成本依然可控。

2、容错的艺术：软间隔与惩罚系数

• 软间隔：允许“不完美”
  现实中总存在一些难以处理的噪声点或离群点。如果为了100%正确分类所有样本（包括噪声），强迫边界做出剧烈弯曲，会导致模型过拟合，在新数据上表现糟糕。软间隔的引入，允许少量样本落在间隔之内甚至被误分类，以此换取更平滑、更泛化的决策边界。
• 惩罚系数 C
  在工程实现中，我们通过一个超参数惩罚系数 C 来控制模型对分类错误的容忍度。C 值越大，模型越倾向于严格分类所有样本，间隔可能变窄；C 值越小，模型对错误更宽容，间隔会更宽。这本质上是一种偏差与方差的权衡艺术。

3、SVM 到底在算什么？

从数学优化角度看，SVM 的训练是一个典型的约束优化问题。

1. 目标函数：最小化 ( \frac{1}{2}||w||^2 )（即最大化间隔）。
2. 约束条件：保证所有样本被正确分类（在软间隔下可略有违反）。
3. 对偶变换：通过拉格朗日乘子法，将原问题转化为更易求解的对偶问题。正是在这个对偶形式中，解会具有“稀疏性”——即大部分拉格朗日乘子为0，非零乘子对应的样本正是支持向量。

这也解释了为何 SVM 在处理如文本分类（词袋模型特征维度极高）、生物信息学（基因序列数据）等 “高维、小样本” 任务时，往往能表现出超越传统方法的稳健性。

限于篇幅，本文重点阐述 SVM 的核心思想与工作机制。关于其背后详细的数学推导与对偶求解过程，我们将在后续文章中独立探讨。

04 终极对比：SVM vs. 逻辑回归 vs. 神经网络

在算法选型或面试讨论中，逻辑回归、支持向量机和神经网络是三个常被对比的分类模型。它们目标相似，但底层逻辑迥异。通过下表，我们可以更清晰地定位 SVM：

维度	逻辑回归 (LR)	支持向量机 (SVM)	神经网络 (NN)
关注点	整体似然最大化（所有点贡献）	局部边界最大化（仅支持向量决定）	拟合复杂非线性函数（所有点参与）
数据量	适合大数据量	适合中小型数据量	数据量越大潜力越大
特征维度	依赖特征工程	擅长处理高维特征	能自动学习特征表示
可解释性	极强（系数代表特征重要性）	较强（决策依据是支持向量）	较差（黑盒模型）
抗噪能力	一般	强（通过软间隔控制）	较强（但可能过拟合噪声）

为什么在当下，SVM 依然有其不可替代的价值？

尽管神经网络，尤其是深度学习，如今风头正劲，但 SVM 在以下场景中依然是“利器”：

• 小样本场景下的稳定性：当训练数据仅有几百或几千条时，神经网络极易过拟合或因优化困难而表现不佳，SVM 则能凭借其最大间隔准则提供更稳定、泛化更好的结果。
• 高维特征处理的优势：在文本分类、生物信息学等领域，特征维度动辄成千上万。SVM 基于间隔最大化的优化目标，其解具有较好的全局性质，不易陷入糟糕的局部最优。
• 模型决策的可解释性：相比于深度神经网络的“黑盒”特性，SVM 的决策过程相对透明——分类边界由少数支持向量定义，分析这些支持向量本身有时就能获得对问题的洞察。

05 写在最后

回到最初的问题：支持向量机，到底在支持什么？

• 在数学层面：它支持的是间隔最大化，寻求最稳健的几何分界。
• 在算法层面：它支持的是抓住主要矛盾，仅由最关键的支持向量决定模型。
• 在哲学与工程层面：它支持的是一种确定性的优雅——即使面对高维的未知空间与有限的样本，只要坚守那条最宽的“安全边界”，便能获得对抗不确定性的强大力量。

SVM 的魅力正在于此：它用简洁而坚实的数学框架，为我们提供了一种在复杂世界中寻找清晰界限的可靠方法。无论是深入理解机器学习的基本原理，还是解决实际的高维分类问题，掌握 SVM 都将为你提供宝贵的视角和工具。在云栈社区，你可以找到更多关于算法原理与实践的深度讨论，与广大开发者一同探索技术的本质。