Transformer架构拆解：编码器-解码器结构与PyTorch实现全解析

Transformer模型可以被视为一个强大的“智能处理器”，它主要由两个部分组成：编码器（Encoder） 和 解码器（Decoder）。

想象一下，编码器像一个阅读器，负责理解和抽象输入的信息；解码器则像一个生成器，将这种抽象理解转化为另一种形式的输出。两者并非单层结构，而是由多层堆叠而成，每一层都进行着复杂的信息加工。

在每一层内部，核心工作是注意力机制（Attention），它决定了哪些信息是关键，应该被重点关注。同时，通过一系列数学运算对信息进行转化和增强。通过这种层层递进的处理，模型能够更好地理解输入数据的内部关系，并生成高质量的输出。

Transformer的工作流程

1. 输入表示：将文本数据转换为数字化的向量表示，并加入位置信息（因为模型本身不具备对顺序的感知）。
2. 编码器堆叠：多层编码器各自关注不同层次的信息特征，通过注意力机制提取全局和局部的重要信息。
3. 解码器堆叠：多层解码器不仅关注已生成的内容，还通过注意力机制融合来自编码器的关键信息，逐步生成最终输出。
4. 输出生成：经过解码器处理后，生成所需的目标序列，例如翻译后的句子。

核心原理

1. Transformer整体架构

Transformer模型由编码器（Encoder）和解码器（Decoder）两个部分组成，它们分别由若干层堆叠而成。

编码器：每一层编码器包含两个子模块：

1. 多头自注意力机制（Multi-Head Self-Attention）
   这部分的主要功能是让模型在处理当前词时，能“看到”序列中其他词的相关信息。
   核心公式：
   [
   \text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V
   ]
   其中，(Q)（Query）、(K)（Key）和(V)（Value）分别是输入经过线性变换后的矩阵；(d_k)是Key的维度，用于缩放以避免数值过大。

2. 前馈神经网络（Feed Forward Neural Network, FFN）
   在自注意力之后，数据会经过一层前馈神经网络，每个位置独立地进行相同的非线性变换。公式一般为：
   [
   FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2
   ]
   这里使用了ReLU激活函数，也可以采用其他激活函数。

解码器：每一层解码器比编码器多一个子模块，主要包括：

1. 掩蔽自注意力机制（Masked Self-Attention）
   与编码器的自注意力类似，但在计算注意力时，未来的词会被屏蔽（mask），确保解码器在生成每个词时只依赖于已生成的部分。

2. 编码器-解码器注意力机制（Encoder-Decoder Attention）
   这一部分让解码器在生成每个词时，都能结合编码器输出的信息。公式与自注意力类似，但输入的Query来自解码器，而Key和Value来自编码器的输出：
   [
   \text{Attention}(Q{dec}, K{enc}, V{enc}) = \text{softmax}(\frac{Q{dec}K_{enc}^T}{\sqrt{dk}})V{enc}
   ]

3. 前馈神经网络（FFN）
   同编码器部分一样，对经过注意力模块处理后的输出进行进一步的非线性转换。

此外，编码器和解码器的每一层都配备了残差连接和层归一化，这两种机制有助于缓解深层网络训练中的梯度消失问题，并提升训练稳定性。

2. 编码器-解码器堆叠结构

在Transformer中，编码器和解码器均由多层堆叠而成。假设编码器堆叠了(N)层，那么每一层都会输出一个中间表示，其中既包含局部信息，也包含全局信息。解码器在每一层中则利用两种注意力机制：首先对当前生成的部分进行自注意力处理，然后将编码器各层的输出作为上下文信息，通过编码器-解码器注意力模块将两部分信息融合。

这种堆叠结构的好处在于：

• 每一层可以抽取不同层次的语义特征，从低级的语法信息到高级的语义信息逐层提炼。
• 残差连接使得信息可以跨层传递，既保留了低层细节，又能够通过多层非线性变换捕捉复杂关系。

3. 信息流动路径

Transformer的信息流动可以从两个角度理解：自注意力内部的信息交互与跨层信息传递。

• 自注意力内部的信息交互：在每个编码器层内，通过自注意力机制，每个输入位置都能与其他位置进行信息交换。例如，在翻译任务中，单词“猫”会自动关注句子中与其相关的其他词，如“毛茸茸”、“宠物”等，从而获得更丰富的上下文信息。这种机制允许模型捕捉长距离依赖，不受固定窗口大小的限制。
• 跨层信息传递：每一层的输出不仅经过当前层的非线性变换，还通过残差连接直接传递给下一层。这样的设计确保了深层信息可以稳定传递，并使得梯度在反向传播时不易消失。层归一化则使每一层的输出均值和方差保持稳定，有助于加速收敛。
• 编码器与解码器之间的信息传递：编码器-解码器注意力模块起到了桥梁作用。它使得解码器在生成输出时，能直接关注编码器中已经提取到的关键信息。例如在翻译中，编码器理解了原句语义，解码器便利用这些信息生成流畅的目标语言句子。

4. 核心公式和推理过程

(1) 多头注意力公式
多头注意力将输入向量分别投影到多个不同的子空间，每个子空间执行一次注意力计算，然后将多个头的结果拼接起来再做一次线性变换。
[
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O
]
其中，每个头的计算为：
[
\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
]
这种设计使得模型可以从不同角度捕捉信息，增强表达能力。

(2) 缩放点积注意力
缩放点积注意力公式（Scaled Dot-Product Attention）是注意力机制的核心：
[
\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V
]
推导思路：

• 内积计算：首先计算Query与所有Key的内积，表示当前词与其他词的相关性。
• 缩放：除以(\sqrt{d_k})主要是为了稳定数值，防止点积值过大使softmax函数进入饱和区。
• softmax归一化：softmax函数将内积结果转化为概率分布，使模型可以“分配”关注的权重。
• 加权求和：最后用这个概率分布对所有Value加权求和，得到融合了全局信息的输出。

(3) 前馈神经网络
前馈神经网络在每个编码器或解码器层中起到非线性变换作用：
[
FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2
]
这部分相当于对每个位置独立处理，通过两层全连接网络进行特征提取与增强。

(4) 残差连接与层归一化
为了避免深层网络训练中梯度消失的问题，Transformer在每个子模块后都添加了残差连接，并随后进行层归一化：
[
\text{LayerNorm}(x + \text{Sublayer}(x))
]
这里，(\text{Sublayer}(x))可以是多头注意力或者FFN的输出。残差连接使得原始输入可以直接传递，同时层归一化保持数据分布稳定。

5. 推理流程实例

假设我们在做机器翻译，输入英文句子 “The cat sat on the mat”。经过输入嵌入和位置编码后，数据进入编码器。

• 第一层编码器：
  每个单词经过多头自注意力，与其他单词建立联系（例如“cat”和“sat”），并通过FFN提取特征。经过残差连接与归一化后，每个单词的表示包含了初步的全局信息。
• 后续编码器层：
  重复上述过程，逐层深化理解，每层都在前一层的基础上提取更加抽象的语义。
• 进入解码器：
  解码器开始生成翻译。首先根据已生成的部分通过掩蔽自注意力构造当前上下文；接着，通过编码器-解码器注意力从编码器获取全局语义信息；最后经过FFN处理，生成当前预测的词。这个过程不断重复，直到生成完整的句子。

在整个过程中，信息从输入到输出经过了多次非线性变换和全局信息交互，确保了最终输出既能保留原始信息的细节，也能捕捉长距离依赖关系，从而生成准确且流畅的翻译结果。如果你对 Transformer 及其在 人工智能 领域的更多应用感兴趣，可以深入探索相关资源。

完整案例：PyTorch实现与可视化分析

以下代码使用 Python 和 PyTorch 实现了 Transformer 的整体架构，包括编码器-解码器堆叠结构与信息流动路径，并使用虚拟数据集进行训练。代码完整展示了数据生成、模型构建、训练和可视化过程。

import torch
import torch.nn as nn
import torch.optim as optim
import math
import numpy as np
import matplotlib.pyplot as plt
import random

# 固定随机种子
torch.manual_seed(42)
np.random.seed(42)
random.seed(42)

# 数据生成部分
# 生成虚拟数据集：以正弦波为例，每个样本为长度为 seq_len 的序列，目标为下一个时刻的值（序列预测问题）
def generate_data(num_samples=1000, seq_len=20):
    X = []
    y = []
    for _ in range(num_samples):
        phase = random.uniform(0, 2 * math.pi)
        # 生成正弦波数据，并添加少量噪声
        seq = np.sin(np.linspace(phase, phase + 3.14, seq_len + 1)) + np.random.normal(0, 0.1, seq_len + 1)
        X.append(seq[:-1])
        y.append(seq[1:])
    X = np.array(X)  # shape: (num_samples, seq_len)
    y = np.array(y)  # shape: (num_samples, seq_len)
    return X, y

# 生成训练集和测试集
train_X, train_y = generate_data(num_samples=800, seq_len=20)
test_X, test_y = generate_data(num_samples=200, seq_len=20)

# 转换为 tensor，并扩展特征维度（feature_dim=1）
train_X = torch.tensor(train_X, dtype=torch.float32).unsqueeze(-1)  # shape: (800, 20, 1)
train_y = torch.tensor(train_y, dtype=torch.float32).unsqueeze(-1)
test_X = torch.tensor(test_X, dtype=torch.float32).unsqueeze(-1)  # shape: (200, 20, 1)
test_y = torch.tensor(test_y, dtype=torch.float32).unsqueeze(-1)

# 位置编码
# 位置编码函数，用于为输入序列添加位置信息
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=500):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)  # shape: (max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float32).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2, dtype=torch.float32) * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(1)  # shape: (max_len, 1, d_model)
        self.register_buffer('pe', pe)

    def forward(self, x):
        # x shape: (seq_len, batch_size, d_model)
        x = x + self.pe[:x.size(0)]
        return self.dropout(x)

# Transformer模型
# 该模型包含编码器和解码器，均堆叠Transformer层，模型用于序列预测
class TransformerModel(nn.Module):
    def __init__(self, feature_size=1, d_model=32, nhead=4, num_encoder_layers=2, num_decoder_layers=2,
                 dim_feedforward=64, dropout=0.1):
        super(TransformerModel, self).__init__()
        self.d_model = d_model

        # 线性映射，将输入特征维度转换为 d_model
        self.input_fc = nn.Linear(feature_size, d_model)
        self.output_fc = nn.Linear(d_model, feature_size)

        self.pos_encoder = PositionalEncoding(d_model, dropout)
        self.pos_decoder = PositionalEncoding(d_model, dropout)

        self.transformer = nn.Transformer(d_model=d_model, nhead=nhead,
                                          num_encoder_layers=num_encoder_layers,
                                          num_decoder_layers=num_decoder_layers,
                                          dim_feedforward=dim_feedforward,
                                          dropout=dropout)

    def forward(self, src, tgt):
        # src 和 tgt shape: (batch_size, seq_len, feature_size)
        # 转置为 (seq_len, batch_size, feature_size)
        src = src.transpose(0, 1)
        tgt = tgt.transpose(0, 1)

        # 输入线性映射到 d_model
        src = self.input_fc(src)
        tgt = self.input_fc(tgt)

        # 添加位置编码
        src = self.pos_encoder(src)
        tgt = self.pos_decoder(tgt)

        # 定义mask：此处简单使用默认mask
        output = self.transformer(src, tgt)
        output = self.output_fc(output)
        # 转置回 (batch_size, seq_len, feature_size)
        output = output.transpose(0, 1)
        return output

# 实例化模型
model = TransformerModel()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 模型训练
num_epochs = 50
batch_size = 32
train_loss_history = []

model.train()
for epoch in range(num_epochs):
    permutation = torch.randperm(train_X.size(0))
    epoch_loss = 0.0
    for i in range(0, train_X.size(0), batch_size):
        indices = permutation[i:i + batch_size]
        batch_src = train_X[indices]  # shape: (batch, seq_len, feature_size)
        batch_tgt = train_y[indices]

        # 为解码器准备输入：使用目标序列的第一个值作为起始（teacher forcing）
        # 这里简单地将目标序列右移一位，并在第一个位置填0
        decoder_input = torch.zeros_like(batch_tgt)
        decoder_input[:, 1:, :] = batch_tgt[:, :-1, :]

        optimizer.zero_grad()
        output = model(batch_src, decoder_input)
        loss = criterion(output, batch_tgt)
        loss.backward()
        optimizer.step()

        epoch_loss += loss.item()
    avg_loss = epoch_loss / (train_X.size(0) / batch_size)
    train_loss_history.append(avg_loss)
    print(f"Epoch {epoch + 1}/{num_epochs} - Loss: {avg_loss:.4f}")

# 模型预测
model.eval()
# 选择一条测试数据进行预测展示
with torch.no_grad():
    test_sample = test_X[0:1]  # shape: (1, seq_len, feature_size)
    true_seq = test_y[0:1].squeeze().cpu().numpy()
    # 构造解码器输入：同训练时处理
    decoder_input = torch.zeros_like(test_sample)
    decoder_input[:, 1:, :] = test_y[0:1, :-1, :]
    pred_seq = model(test_sample, decoder_input).squeeze().cpu().numpy()

# 模拟注意力权重
# 为了展示 Transformer 内部信息流动，这里模拟一个注意力热图（实际项目中可通过hook获取真实注意力）
attn_weights = np.random.rand(20, 20)  # 假设序列长度为20

# 数据分析图
plt.figure(figsize=(16, 12))

# 子图1：训练损失曲线
plt.subplot(2, 2, 1)
plt.plot(range(1, num_epochs + 1), train_loss_history, marker='o', color='crimson', linewidth=2)
plt.xlabel("Epoch", fontsize=12)  # label in English
plt.ylabel("Loss", fontsize=12)  # label in English
plt.title("Training Loss Curve", fontsize=14)  # title in English
plt.grid(True)

# 子图2：预测曲线与真实曲线对比
plt.subplot(2, 2, 2)
plt.plot(true_seq, marker='o', linestyle='-', color='navy', label='True')
plt.plot(pred_seq, marker='x', linestyle='--', color='darkorange', label='Predicted')
plt.xlabel("Time Step", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.title("Prediction vs Ground Truth", fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)

# 子图3：模拟注意力权重热图
plt.subplot(2, 2, 3)
plt.imshow(attn_weights, cmap='hot', interpolation='nearest')
plt.xlabel("Key Position", fontsize=12)
plt.ylabel("Query Position", fontsize=12)
plt.title("Attention Heatmap", fontsize=14)
plt.colorbar()

# 子图4：输入数据分布直方图
plt.subplot(2, 2, 4)
# 将所有训练数据的值汇总绘制直方图
plt.hist(train_X.cpu().numpy().flatten(), bins=30, color='mediumseagreen', edgecolor='black')
plt.xlabel("Input Value", fontsize=12)
plt.ylabel("Frequency", fontsize=12)
plt.title("Input Data Distribution", fontsize=14)
plt.grid(True)

plt.tight_layout()
plt.show()

运行上述代码后，会生成一张包含四个子图的分析图表，直观展示模型训练与运行效果：

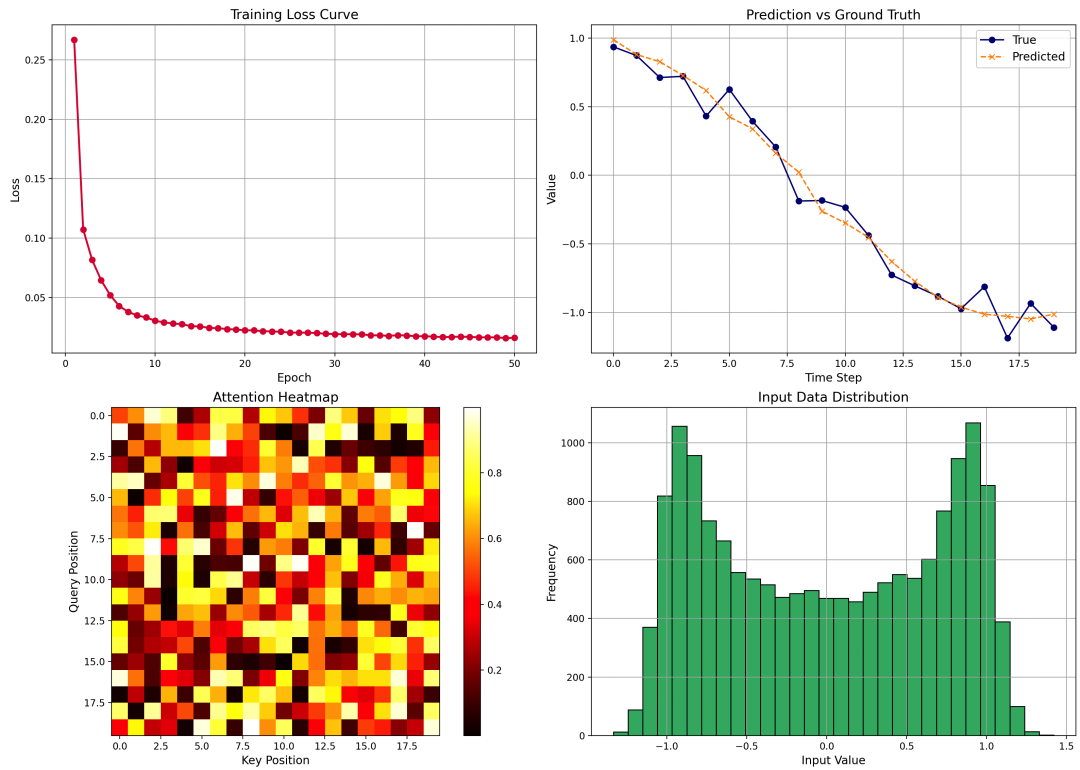
1. Training Loss Curve（训练损失曲线）：展示了训练过程中模型损失随 epoch 变化的趋势，用以观察模型是否收敛。
2. Prediction vs Ground Truth（预测值与真实值对比）：在测试样本上对比模型的预测序列与真实序列，可以直观评估模型的预测效果。
3. Attention Heatmap（注意力热力图）：模拟了 Transformer 编码器中注意力权重的分布情况，反映了信息在序列内部流动的路径。请注意，此处为模拟数据，在实际应用中可以通过 hook 获取真实的注意力矩阵。
4. Input Data Distribution（输入数据分布）：展示了训练数据输入值的分布情况，有助于了解数据的统计特性，为数据预处理提供依据。

通过这个完整的案例，我们不仅理解了 Transformer 的理论架构，还动手实现了一个简易的序列预测模型，并通过可视化手段分析了其内部工作状态。希望这篇文章能帮助你透彻理解 Transformer 这一强大的算法模型。更多关于机器学习和深度学习的实战讨论，欢迎在 云栈社区 交流分享。