注意:本文基于早期PyTorch版本实现。最新版本请访问 官方更新版本
《Attention is All You Need》论文提出的 Transformer 架构在过去一年引起了广泛关注。除了在翻译质量上取得重大突破外,它还为众多自然语言处理任务提供了全新的架构思路。尽管论文本身写得非常清晰,但业界普遍认为正确实现该模型具有一定难度。
本文以"带注释"的形式呈现论文内容,提供逐行代码实现。我们对原论文的部分章节进行了重新排序和删减,并在关键位置添加了详细注释。整个文档本身就是一个可运行的 Jupyter Notebook,包含约 400 行核心代码,在 4 块 GPU 上可达到每秒处理 27,000 个 token 的速度。
环境准备
首先需要安装 PyTorch。完整的 notebook 可以在 GitHub 或 Google Colab(提供免费 GPU)上获取。
本文旨在为研究人员和开发者提供起点。代码主要基于我们的 OpenNMT 项目。如需完整的生产级实现,可参考 Tensor2Tensor(TensorFlow)和 Sockeye(MXNet)。
作者: Alexander Rush (@harvardnlp 或 srush@seas.harvard.edu),协助者:Vincent Nguyen 和 Guillaume Klein
依赖库导入
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn
seaborn.set_context(context="talk")
%matplotlib inline
背景知识
减少序列计算也是 Extended Neural GPU、ByteNet 和 ConvS2S 的核心目标,这些模型都使用卷积神经网络作为基础模块,并行计算所有输入和输出位置的隐藏表示。在这些模型中,关联两个任意位置信号所需的操作数量随位置距离增长——ConvS2S 呈线性增长,ByteNet 呈对数增长。这使得学习远距离依赖关系变得更加困难。而在 Transformer 中,这被减少到常数次操作,尽管会因注意力权重平均而降低有效分辨率,但我们通过多头注意力机制来抵消这一影响。
自注意力(Self-attention),有时也称为内部注意力(intra-attention),是一种将单个序列的不同位置关联起来以计算序列表示的注意力机制。自注意力已成功应用于阅读理解、抽象摘要、文本蕴含和任务无关的句子表示学习等多个任务。端到端记忆网络基于循环注意力机制而非序列对齐的循环结构,在简单语言问答和语言建模任务上表现出色。
据我们所知,Transformer 是第一个完全依赖自注意力来计算输入输出表示的转换模型,无需使用序列对齐的 RNN 或卷积。
模型架构
大多数竞争性的神经序列转换模型都采用编码器-解码器结构。编码器将输入符号序列 [(x_1, …, x_n)] 映射为连续表示序列 [\mathbf{z} = (z_1, …, z_n)]。给定 [\mathbf{z}],解码器逐个生成输出序列 [(y_1,…,y_m)]。模型在每个时间步都是自回归的,即生成下一个符号时会将之前生成的符号作为额外输入。
class EncoderDecoder(nn.Module):
"""
标准的编码器-解码器架构,是本模型和许多其他模型的基础
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
"处理带掩码的源序列和目标序列"
return self.decode(self.encode(src, src_mask), src_mask,
tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
class Generator(nn.Module):
"定义标准的线性层 + softmax 生成步骤"
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)
Transformer 遵循这一整体架构,编码器和解码器都使用堆叠的自注意力层和逐位置的全连接层,如下图所示。
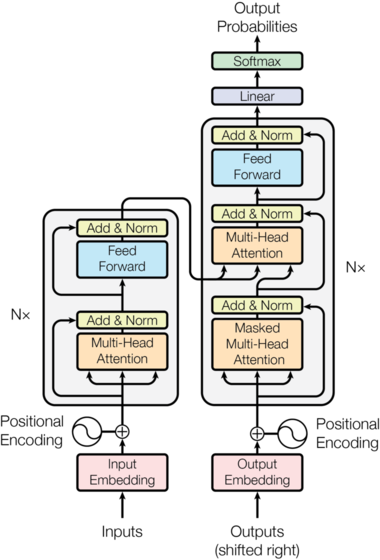
编码器和解码器堆栈
编码器
编码器由 [N=6] 个相同的层堆叠而成。
def clones(module, N):
"生成 N 个相同的层"
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
"核心编码器是 N 层的堆叠"
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"依次通过每一层(包括掩码)"
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
我们在每个子层周围使用残差连接,然后进行层归一化。
class LayerNorm(nn.Module):
"构建层归一化模块"
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
也就是说,每个子层的输出是 [\mathrm{LayerNorm}(x + \mathrm{Sublayer}(x))],其中 [\mathrm{Sublayer}(x)] 是子层自身实现的函数。我们在每个子层输出上应用 dropout,然后再与子层输入相加并归一化。
为了便于这些残差连接,模型中的所有子层以及嵌入层都产生维度为 [d_{\text{model}}=512] 的输出。
class SublayerConnection(nn.Module):
"""
残差连接后接层归一化
注意:为了代码简洁,这里先进行归一化而非最后归一化
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"对任何具有相同大小的子层应用残差连接"
return x + self.dropout(sublayer(self.norm(x)))
每层包含两个子层。第一个是多头自注意力机制,第二个是简单的逐位置全连接前馈网络。
class EncoderLayer(nn.Module):
"编码器由自注意力层和前馈网络组成"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
"按照图 1(左)的连接方式"
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
解码器
解码器同样由 [N=6] 个相同的层堆叠而成。
class Decoder(nn.Module):
"通用的带掩码的 N 层解码器"
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
除了每个编码器层中的两个子层外,解码器还插入了第三个子层,对编码器堆栈的输出执行多头注意力。与编码器类似,我们在每个子层周围使用残差连接,然后进行层归一化。
class DecoderLayer(nn.Module):
"解码器由自注意力、源注意力和前馈网络组成"
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
"按照图 1(右)的连接方式"
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
我们还修改了解码器堆栈中的自注意力子层,以防止位置关注到后续位置。这种掩码与输出嵌入偏移一个位置的事实相结合,确保对位置 [i] 的预测只能依赖于小于 [i] 的已知输出。
def subsequent_mask(size):
"掩盖后续位置"
attn_shape = (1, size, size)
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(subsequent_mask) == 0
下面的注意力掩码显示了每个目标词(行)允许查看的位置(列)。在训练期间,词被阻止关注未来的词。
plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(20)[0])
None

注意力机制
注意力函数可以描述为将查询(query)和一组键值对(key-value pairs)映射到输出,其中查询、键、值和输出都是向量。输出是值的加权和,其中分配给每个值的权重由查询与相应键的兼容性函数计算得出。
我们将这种特殊的注意力称为"缩放点积注意力"。输入包括维度为 [d_k] 的查询和键,以及维度为 [d_v] 的值。我们计算查询与所有键的点积,除以 [\sqrt{d_k}],然后应用 softmax 函数获得值的权重。
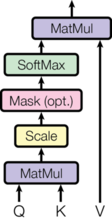
在实践中,我们同时对一组查询计算注意力函数,将它们打包成矩阵 [Q]。键和值也被打包成矩阵 [K] 和 [V]。我们计算输出矩阵为:
[\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V]
def attention(query, key, value, mask=None, dropout=None):
"计算缩放点积注意力"
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
两种最常用的注意力函数是加性注意力和点积(乘性)注意力。点积注意力与我们的算法相同,只是缺少缩放因子 [\frac{1}{\sqrt{d_k}}]。加性注意力使用具有单个隐藏层的前馈网络计算兼容性函数。虽然两者在理论复杂度上相似,但点积注意力在实践中更快且更节省空间,因为可以使用高度优化的矩阵乘法代码实现。
对于较小的 [d_k] 值,两种机制性能相似;但对于较大的 [d_k] 值,加性注意力优于无缩放的点积注意力。我们怀疑对于较大的 [d_k],点积的幅度会变大,将 softmax 函数推入梯度极小的区域。为了抵消这种影响,我们将点积缩放 [\frac{1}{\sqrt{d_k}}]。
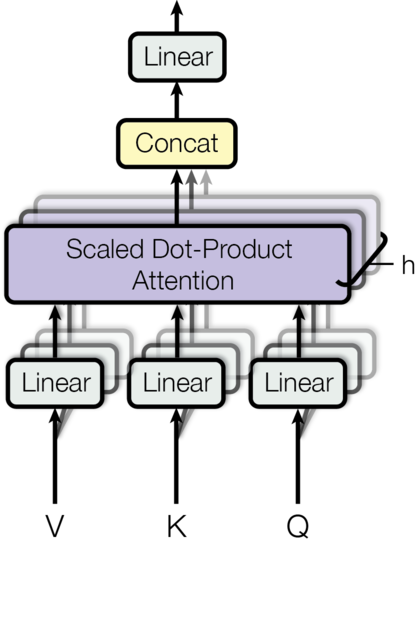
多头注意力允许模型在不同位置联合关注来自不同表示子空间的信息。使用单个注意力头时,平均化会抑制这一点。
[\mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O]
其中 [\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i)]
投影参数矩阵为 [W^Qi \in \mathbb{R}^{d{\text{model}} \times d_k}]、[W^Ki \in \mathbb{R}^{d{\text{model}} \times d_k}]、[W^Vi \in \mathbb{R}^{d{\text{model}} \times d_v}] 和 [W^O \in \mathbb{R}^{hdv \times d{\text{model}}}]。
在本工作中,我们使用 [h=8] 个并行的注意力层或注意力头。对于每个头,我们使用 [d_k=dv=d{\text{model}}/h=64]。由于每个头的维度减少,总计算成本与具有完整维度的单头注意力相似。
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
"接收模型大小和注意力头数"
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# 我们假设 d_v 始终等于 d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
"实现图 2"
if mask is not None:
# 对所有 h 个头应用相同的掩码
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) 批量执行所有线性投影:d_model => h x d_k
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) 批量对所有投影向量应用注意力
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) 使用视图"拼接"并应用最终线性层
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
模型中注意力的应用
Transformer 以三种不同方式使用多头注意力:
1) 在"编码器-解码器注意力"层中,查询来自前一个解码器层,而记忆键和值来自编码器的输出。这允许解码器中的每个位置关注输入序列中的所有位置,模仿了典型的序列到序列模型中的编码器-解码器注意力机制。
2) 编码器包含自注意力层。在自注意力层中,所有的键、值和查询都来自同一个地方,即编码器中前一层的输出。编码器中的每个位置都可以关注编码器前一层中的所有位置。
3) 类似地,解码器中的自注意力层允许解码器中的每个位置关注解码器中直到并包括该位置的所有位置。我们需要防止解码器中的信息向左流动,以保持自回归特性。我们通过在缩放点积注意力内部屏蔽(设置为 [-\infty])softmax 输入中对应于非法连接的所有值来实现这一点。
逐位置前馈网络
除了注意力子层外,编码器和解码器中的每一层都包含一个全连接前馈网络,该网络分别且相同地应用于每个位置。它由两个线性变换组成,中间有一个 ReLU 激活函数。
[\mathrm{FFN}(x)=\max(0, xW_1 + b_1) W_2 + b_2]
虽然线性变换在不同位置上是相同的,但它们在不同层之间使用不同的参数。另一种描述方式是将其视为核大小为 1 的两个卷积。输入和输出的维度是 [d{\text{model}}=512],内层的维度是 [d{ff}=2048]。
class PositionwiseFeedForward(nn.Module):
"实现 FFN 公式"
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
嵌入和 Softmax
与其他序列转换模型类似,我们使用学习到的嵌入将输入 token 和输出 token 转换为维度 [d{\text{model}}] 的向量。我们还使用常规的学习线性变换和 softmax 函数将解码器输出转换为预测的下一个 token 概率。在我们的模型中,我们在两个嵌入层和 pre-softmax 线性变换之间共享相同的权重矩阵。在嵌入层中,我们将这些权重乘以 [\sqrt{d{\text{model}}}]。
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
位置编码
由于我们的模型不包含循环和卷积,为了让模型利用序列的顺序,我们必须注入一些关于 token 在序列中的相对或绝对位置的信息。为此,我们在编码器和解码器堆栈底部的输入嵌入中添加"位置编码"。位置编码具有与嵌入相同的维度 [d_{\text{model}}],因此两者可以相加。位置编码有多种选择,包括学习的和固定的。
在本工作中,我们使用不同频率的正弦和余弦函数:
[PE{(pos,2i)} = sin(pos / 10000^{2i/d{\text{model}}})]
[PE{(pos,2i+1)} = cos(pos / 10000^{2i/d{\text{model}}})]
其中 [pos] 是位置,[i] 是维度。也就是说,位置编码的每个维度对应一个正弦曲线。波长形成从 [2\pi] 到 [10000 \cdot 2\pi] 的几何级数。我们选择这个函数是因为我们假设它可以让模型轻松学习通过相对位置进行关注,因为对于任何固定偏移 [k],[PE{pos+k}] 可以表示为 [PE{pos}] 的线性函数。
此外,我们在编码器和解码器堆栈中对嵌入和位置编码的总和应用 dropout。对于基础模型,我们使用 [P_{drop}=0.1] 的比率。
class PositionalEncoding(nn.Module):
"实现 PE 函数"
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# 在对数空间中一次性计算位置编码
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
return self.dropout(x)
下面的位置编码将根据位置添加正弦波。波的频率和偏移对于每个维度都不同。
plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)
y = pe.forward(Variable(torch.zeros(1, 100, 20)))
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4,5,6,7]])
None
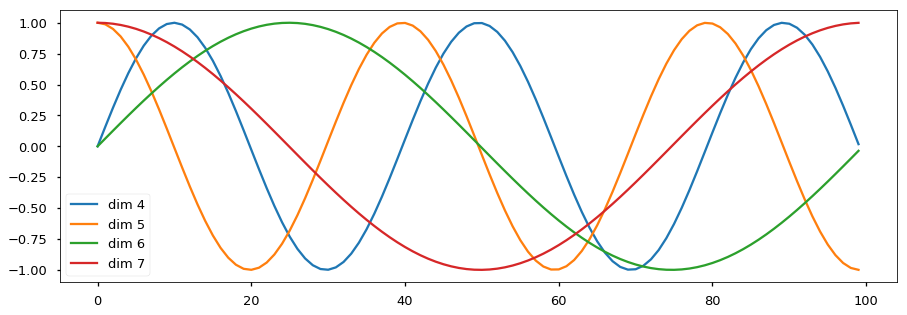
我们还尝试使用学习的位置嵌入,发现两个版本产生了几乎相同的结果。我们选择正弦版本是因为它可能允许模型外推到比训练期间遇到的序列更长的序列长度。
完整模型
这里我们定义一个函数,它接受超参数并生成完整模型。
def make_model(src_vocab, tgt_vocab, N=6,
d_model=512, d_ff=2048, h=8, dropout=0.1):
"根据超参数构建模型的辅助函数"
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn),
c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# 这一点很重要,使用 Glorot / fan_avg 初始化参数
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
# 小型示例模型
tmp_model = make_model(10, 10, 2)
None
训练
本节描述我们模型的训练机制。
我们暂停一下,介绍训练标准编码器-解码器模型所需的一些工具。首先定义一个批次对象,用于在训练期间保存源句子和目标句子,以及构建掩码。
批次和掩码
class Batch:
"在训练期间保存带掩码的批次数据的对象"
def __init__(self, src, trg=None, pad=0):
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if trg is not None:
self.trg = trg[:, :-1]
self.trg_y = trg[:, 1:]
self.trg_mask = \
self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).data.sum()
@staticmethod
def make_std_mask(tgt, pad):
"创建掩码以隐藏填充和未来词"
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & Variable(
subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
return tgt_mask
接下来,我们创建一个通用的训练和评分函数来跟踪损失。我们传入一个通用的损失计算函数,该函数还处理参数更新。
训练循环
def run_epoch(data_iter, model, loss_compute):
"标准的训练和日志记录函数"
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for i, batch in enumerate(data_iter):
out = model.forward(batch.src, batch.trg,
batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print("Epoch Step: %d Loss: %f Tokens per Sec: %f" %
(i, loss / batch.ntokens, tokens / elapsed))
start = time.time()
tokens = 0
return total_loss / total_tokens
训练数据和批处理
我们在标准的 WMT 2014 英德数据集上进行训练,该数据集包含约 450 万个句子对。句子使用字节对编码进行编码,具有约 37000 个 token 的共享源-目标词汇表。对于英法翻译,我们使用更大的 WMT 2014 英法数据集,包含 3600 万个句子,并将 token 分割为 32000 个词片段词汇表。
句子对按近似序列长度进行批处理。每个训练批次包含一组句子对,包含大约 25000 个源 token 和 25000 个目标 token。
我们将使用 torchtext 进行批处理。这将在下面详细讨论。这里我们创建批次的方式确保我们的批次大小(填充到最大批次大小)不超过阈值(如果我们有 8 个 GPU,则为 25000)。
global max_src_in_batch, max_tgt_in_batch
def batch_size_fn(new, count, sofar):
"不断增加批次并计算 token 总数 + 填充"
global max_src_in_batch, max_tgt_in_batch
if count == 1:
max_src_in_batch = 0
max_tgt_in_batch = 0
max_src_in_batch = max(max_src_in_batch, len(new.src))
max_tgt_in_batch = max(max_tgt_in_batch, len(new.trg) + 2)
src_elements = count * max_src_in_batch
tgt_elements = count * max_tgt_in_batch
return max(src_elements, tgt_elements)
硬件和训练计划
我们在一台配备 8 块 NVIDIA P100 GPU 的机器上训练模型。对于使用整篇论文中描述的超参数的基础模型,每个训练步骤大约需要 0.4 秒。我们训练基础模型总共 100,000 步或 12 小时。对于大型模型,步骤时间为 1.0 秒。大型模型训练了 300,000 步(3.5 天)。
优化器
我们使用 Adam 优化器,参数为 [\beta_1=0.9]、[\beta_2=0.98] 和 [\epsilon=10^{-9}]。我们在训练过程中根据以下公式改变学习率:
[lrate = d_{\text{model}}^{-0.5} \cdot \min({step_num}^{-0.5}, {step_num} \cdot {warmup_steps}^{-1.5})]
这对应于在前 [warmup_steps] 个训练步骤中线性增加学习率,然后按步骤数的平方根倒数成比例地降低学习率。我们使用 [warmup_steps=4000]。
注意:这部分非常重要。需要使用此设置训练模型。
class NoamOpt:
"实现学习率的优化器包装器"
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self):
"更新参数和学习率"
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step = None):
"实现上面的 lrate 公式"
if step is None:
step = self._step
return self.factor * \
(self.model_size ** (-0.5) *
min(step ** (-0.5), step * self.warmup ** (-1.5)))
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
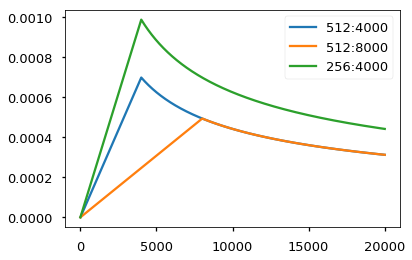
下面是不同模型大小和优化超参数的学习率曲线示例。
# 三种学习率超参数设置
opts = [NoamOpt(512, 1, 4000, None),
NoamOpt(512, 1, 8000, None),
NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
None
正则化
标签平滑
在训练期间,我们采用值为 [\epsilon_{ls}=0.1] 的标签平滑。这会损害困惑度,因为模型学会了更加不确定,但提高了准确性和 BLEU 分数。
我们使用 KL 散度损失实现标签平滑。我们不使用 one-hot 目标分布,而是创建一个分布,该分布对正确词具有 confidence,并将其余的 smoothing 质量分布在整个词汇表中。
class LabelSmoothing(nn.Module):
"实现标签平滑"
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(size_average=False)
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
assert x.size(1) == self.size
true_dist = x.data.clone()
true_dist.fill_(self.smoothing / (self.size - 2))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target.data == self.padding_idx)
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
return self.criterion(x, Variable(true_dist, requires_grad=False))
这里我们可以看到基于置信度如何将质量分配给词。
# 标签平滑示例
crit = LabelSmoothing(5, 0, 0.4)
predict = torch.FloatTensor([[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0]])
v = crit(Variable(predict.log()),
Variable(torch.LongTensor([2, 1, 0])))
# 显示系统期望的目标分布
plt.imshow(crit.true_dist)
None

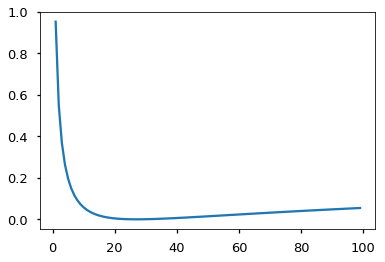
如果模型对给定选择非常有信心,标签平滑实际上会开始惩罚模型。
crit = LabelSmoothing(5, 0, 0.1)
def loss(x):
d = x + 3 * 1
predict = torch.FloatTensor([[0, x / d, 1 / d, 1 / d, 1 / d],
])
return crit(Variable(predict.log()),
Variable(torch.LongTensor([1]))).data[0]
plt.plot(np.arange(1, 100), [loss(x) for x in range(1, 100)])
None
第一个示例
我们可以从尝试一个简单的复制任务开始。给定来自小词汇表的随机输入符号集,目标是生成回这些相同的符号。
合成数据
def data_gen(V, batch, nbatches):
"为源-目标复制任务生成随机数据"
for i in range(nbatches):
data = torch.from_numpy(np.random.randint(1, V, size=(batch, 10)))
data[:, 0] = 1
src = Variable(data, requires_grad=False)
tgt = Variable(data, requires_grad=False)
yield Batch(src, tgt, 0)
损失计算
class SimpleLossCompute:
"简单的损失计算和训练函数"
def __init__(self, generator, criterion, opt=None):
self.generator = generator
self.criterion = criterion
self.opt = opt
def __call__(self, x, y, norm):
x = self.generator(x)
loss = self.criterion(x.contiguous().view(-1, x.size(-1)),
y.contiguous().view(-1)) / norm
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
return loss.data[0] * norm
贪婪解码
# 训练简单的复制任务
V = 11
criterion = LabelSmoothing(size=V, padding_idx=0, smoothing=0.0)
model = make_model(V, V, N=2)
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 400,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
for epoch in range(10):
model.train()
run_epoch(data_gen(V, 30, 20), model,
SimpleLossCompute(model.generator, criterion, model_opt))
model.eval()
print(run_epoch(data_gen(V, 30, 5), model,
SimpleLossCompute(model.generator, criterion, None)))
此代码使用贪婪解码预测翻译以简化操作。
def greedy_decode(model, src, src_mask, max_len, start_symbol):
memory = model.encode(src, src_mask)
ys = torch.ones(1, 1).fill_(start_symbol).type_as(src.data)
for i in range(max_len-1):
out = model.decode(memory, src_mask,
Variable(ys),
Variable(subsequent_mask(ys.size(1))
.type_as(src.data)))
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim = 1)
next_word = next_word.data[0]
ys = torch.cat([ys,
torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=1)
return ys
model.eval()
src = Variable(torch.LongTensor([[1,2,3,4,5,6,7,8,9,10]]) )
src_mask = Variable(torch.ones(1, 1, 10) )
print(greedy_decode(model, src, src_mask, max_len=10, start_symbol=1))
真实世界示例
现在我们考虑使用 IWSLT 德英翻译任务的真实世界示例。该任务比论文中考虑的 WMT 任务小得多,但它展示了整个系统。我们还展示了如何使用多 GPU 处理使其真正快速。
数据加载
我们将使用 torchtext 和 spacy 进行分词来加载数据集。
# 用于数据加载
from torchtext import data, datasets
if True:
import spacy
spacy_de = spacy.load('de')
spacy_en = spacy.load('en')
def tokenize_de(text):
return [tok.text for tok in spacy_de.tokenizer(text)]
def tokenize_en(text):
return [tok.text for tok in spacy_en.tokenizer(text)]
BOS_WORD = '<s>'
EOS_WORD = '</s>'
BLANK_WORD = "<blank>"
SRC = data.Field(tokenize=tokenize_de, pad_token=BLANK_WORD)
TGT = data.Field(tokenize=tokenize_en, init_token = BOS_WORD,
eos_token = EOS_WORD, pad_token=BLANK_WORD)
MAX_LEN = 100
train, val, test = datasets.IWSLT.splits(
exts=('.de', '.en'), fields=(SRC, TGT),
filter_pred=lambda x: len(vars(x)['src']) <= MAX_LEN and
len(vars(x)['trg']) <= MAX_LEN)
MIN_FREQ = 2
SRC.build_vocab(train.src, min_freq=MIN_FREQ)
TGT.build_vocab(train.trg, min_freq=MIN_FREQ)
批处理对速度至关重要。我们希望有非常均匀分割的批次,填充绝对最小。为此,我们必须对默认的 torchtext 批处理进行一些修改。此代码修补了它们的默认批处理,以确保我们搜索足够多的句子以找到紧密的批次。
迭代器
class MyIterator(data.Iterator):
def create_batches(self):
if self.train:
def pool(d, random_shuffler):
for p in data.batch(d, self.batch_size * 100):
p_batch = data.batch(
sorted(p, key=self.sort_key),
self.batch_size, self.batch_size_fn)
for b in random_shuffler(list(p_batch)):
yield b
self.batches = pool(self.data(), self.random_shuffler)
else:
self.batches = []
for b in data.batch(self.data(), self.batch_size,
self.batch_size_fn):
self.batches.append(sorted(b, key=self.sort_key))
def rebatch(pad_idx, batch):
"修正 torchtext 中的顺序以匹配我们的顺序"
src, trg = batch.src.transpose(0, 1), batch.trg.transpose(0, 1)
return Batch(src, trg, pad_idx)
多 GPU 训练
最后,为了真正实现快速训练,我们将使用多 GPU。此代码实现了多 GPU 词生成。它不是 Transformer 特有的,所以我不会详细介绍。这个想法是在训练时将词生成分成块,以便在许多不同的 GPU 上并行处理。我们使用 PyTorch 并行原语来实现:
- replicate - 将模块分割到不同的 GPU 上
- scatter - 将批次分割到不同的 GPU 上
- parallel_apply - 在不同的 GPU 上将模块应用于批次
- gather - 将分散的数据拉回到一个 GPU 上
- nn.DataParallel - 一个特殊的模块包装器,在评估之前调用所有这些
# 如果对多 GPU 不感兴趣可以跳过
class MultiGPULossCompute:
"多 GPU 损失计算和训练函数"
def __init__(self, generator, criterion, devices, opt=None, chunk_size=5):
# 发送到不同的 GPU
self.generator = generator
self.criterion = nn.parallel.replicate(criterion,
devices=devices)
self.opt = opt
self.devices = devices
self.chunk_size = chunk_size
def __call__(self, out, targets, normalize):
total = 0.0
generator = nn.parallel.replicate(self.generator,
devices=self.devices)
out_scatter = nn.parallel.scatter(out,
target_gpus=self.devices)
out_grad = [[] for _ in out_scatter]
targets = nn.parallel.scatter(targets,
target_gpus=self.devices)
# 将生成分成块
chunk_size = self.chunk_size
for i in range(0, out_scatter[0].size(1), chunk_size):
# 预测分布
out_column = [[Variable(o[:, i:i+chunk_size].data,
requires_grad=self.opt is not None)]
for o in out_scatter]
gen = nn.parallel.parallel_apply(generator, out_column)
# 计算损失
y = [(g.contiguous().view(-1, g.size(-1)),
t[:, i:i+chunk_size].contiguous().view(-1))
for g, t in zip(gen, targets)]
loss = nn.parallel.parallel_apply(self.criterion, y)
# 求和并归一化损失
l = nn.parallel.gather(loss,
target_device=self.devices[0])
l = l.sum()[0] / normalize
total += l.data[0]
# 将损失反向传播到 Transformer 的输出
if self.opt is not None:
l.backward()
for j, l in enumerate(loss):
out_grad[j].append(out_column[j][0].grad.data.clone())
# 通过 Transformer 反向传播所有损失
if self.opt is not None:
out_grad = [Variable(torch.cat(og, dim=1)) for og in out_grad]
o1 = out
o2 = nn.parallel.gather(out_grad,
target_device=self.devices[0])
o1.backward(gradient=o2)
self.opt.step()
self.opt.optimizer.zero_grad()
return total * normalize
现在我们创建模型、损失函数、优化器、数据迭代器和并行化
# 要使用的 GPU
devices = [0, 1, 2, 3]
if True:
pad_idx = TGT.vocab.stoi["<blank>"]
model = make_model(len(SRC.vocab), len(TGT.vocab), N=6)
model.cuda()
criterion = LabelSmoothing(size=len(TGT.vocab), padding_idx=pad_idx, smoothing=0.1)
criterion.cuda()
BATCH_SIZE = 12000
train_iter = MyIterator(train, batch_size=BATCH_SIZE, device=0,
repeat=False, sort_key=lambda x: (len(x.src), len(x.trg)),
batch_size_fn=batch_size_fn, train=True)
valid_iter = MyIterator(val, batch_size=BATCH_SIZE, device=0,
repeat=False, sort_key=lambda x: (len(x.src), len(x.trg)),
batch_size_fn=batch_size_fn, train=False)
model_par = nn.DataParallel(model, device_ids=devices)
None
现在我们训练模型。我会调整一下预热步骤,但其他所有内容都使用默认参数。在配备 4 块 Tesla V100 的 AWS p3.8xlarge 上,批次大小为 12,000 时,运行速度约为每秒 27,000 个 token
训练系统
if False:
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 2000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
for epoch in range(10):
model_par.train()
run_epoch((rebatch(pad_idx, b) for b in train_iter),
model_par,
MultiGPULossCompute(model.generator, criterion,
devices=devices, opt=model_opt))
model_par.eval()
loss = run_epoch((rebatch(pad_idx, b) for b in valid_iter),
model_par,
MultiGPULossCompute(model.generator, criterion,
devices=devices, opt=None))
print(loss)
else:
model = torch.load("iwslt.pt")
训练完成后,我们可以解码模型以生成一组翻译。这里我们简单地翻译验证集中的第一个句子。由于该数据集相当小,使用贪婪搜索的翻译相当准确。
for i, batch in enumerate(valid_iter):
src = batch.src.transpose(0, 1)[:1]
src_mask = (src != SRC.vocab.stoi["<blank>"]).unsqueeze(-2)
out = greedy_decode(model, src, src_mask,
max_len=60, start_symbol=TGT.vocab.stoi["<s>"])
print("Translation:", end="\t")
for i in range(1, out.size(1)):
sym = TGT.vocab.itos[out[0, i]]
if sym == "</s>": break
print(sym, end =" ")
print()
print("Target:", end="\t")
for i in range(1, batch.trg.size(0)):
sym = TGT.vocab.itos[batch.trg.data[i, 0]]
if sym == "</s>": break
print(sym, end =" ")
print()
break
额外组件:BPE、搜索、平均
这主要涵盖了 Transformer 模型本身。我们没有明确涵盖四个方面。我们在 OpenNMT-py 中实现了所有这些额外功能。
1) BPE / 词片段:我们可以使用库首先将数据预处理为子词单元。请参阅 Rico Sennrich 的 subword-nmt 实现。这些模型将转换训练数据,使其看起来像这样:
▁Die ▁Protokoll datei ▁kann ▁ heimlich ▁per ▁E - Mail ▁oder ▁FTP ▁an ▁einen ▁bestimmte n ▁Empfänger ▁gesendet ▁werden .
2) 共享嵌入:当使用具有共享词汇表的 BPE 时,我们可以在源/目标/生成器之间共享相同的权重向量。有关详细信息,请参阅论文。要将其添加到模型中,只需执行以下操作:
if False:
model.src_embed[0].lut.weight = model.tgt_embeddings[0].lut.weight
model.generator.lut.weight = model.tgt_embed[0].lut.weight
3) 束搜索:这有点太复杂,无法在此处涵盖。请参阅 OpenNMT-py 的 PyTorch 实现。
4) 模型平均:论文对最后 k 个检查点进行平均以创建集成效果。如果我们有一堆模型,可以在事后执行此操作:
def average(model, models):
"将模型平均到 model 中"
for ps in zip(*[m.params() for m in [model] + models]):
p[0].copy_(torch.sum(*ps[1:]) / len(ps[1:]))
结果
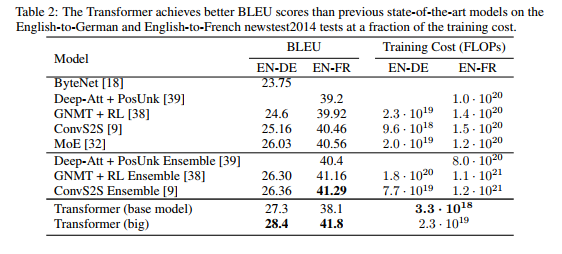
在 WMT 2014 英德翻译任务上,大型 Transformer 模型(表 2 中的 Transformer (big))的表现优于之前报告的最佳模型(包括集成)超过 2.0 BLEU,建立了新的最先进的 BLEU 分数 28.4。该模型的配置列在表 3 的底行。训练在 8 块 P100 GPU 上花费了 3.5 天。即使是我们的基础模型也超越了所有先前发布的模型和集成,训练成本只是任何竞争模型的一小部分。
在 WMT 2014 英法翻译任务上,我们的大型模型达到了 41.0 的 BLEU 分数,优于所有先前发布的单一模型,训练成本不到先前最先进模型的 1/4。用于英法翻译的 Transformer (big) 模型使用 dropout 率 Pdrop = 0.1,而不是 0.3。
我们在这里编写的代码是基础模型的一个版本。这里有该系统的完全训练版本 示例模型。
通过最后一节中的额外扩展,OpenNMT-py 复制在 EN-DE WMT 上达到了 26.9。这里我已将这些参数加载到我们的重新实现中。
model, SRC, TGT = torch.load("en-de-model.pt")
model.eval()
sent = "▁The ▁log ▁file ▁can ▁be ▁sent ▁secret ly ▁with ▁email ▁or ▁FTP ▁to ▁a ▁specified ▁receiver".split()
src = torch.LongTensor([[SRC.stoi[w] for w in sent]])
src = Variable(src)
src_mask = (src != SRC.stoi["<blank>"]).unsqueeze(-2)
out = greedy_decode(model, src, src_mask,
max_len=60, start_symbol=TGT.stoi["<s>"])
print("Translation:", end="\t")
trans = "<s> "
for i in range(1, out.size(1)):
sym = TGT.itos[out[0, i]]
if sym == "</s>": break
trans += sym + " "
print(trans)
Translation: <s> ▁Die ▁Protokoll datei ▁kann ▁ heimlich ▁per ▁E - Mail ▁oder ▁FTP ▁an ▁einen ▁bestimmte n ▁Empfänger ▁gesendet ▁werden .
注意力可视化
即使使用贪婪解码器,翻译看起来也相当不错。我们可以进一步可视化它,以查看每层注意力发生了什么
tgt_sent = trans.split()
def draw(data, x, y, ax):
seaborn.heatmap(data,
xticklabels=x, square=True, yticklabels=y, vmin=0.0, vmax=1.0,
cbar=False, ax=ax)
for layer in range(1, 6, 2):
fig, axs = plt.subplots(1,4, figsize=(20, 10))
print("Encoder Layer", layer+1)
for h in range(4):
draw(model.encoder.layers[layer].self_attn.attn[0, h].data,
sent, sent if h ==0 else [], ax=axs[h])
plt.show()
for layer in range(1, 6, 2):
fig, axs = plt.subplots(1,4, figsize=(20, 10))
print("Decoder Self Layer", layer+1)
for h in range(4):
draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(tgt_sent)],
tgt_sent, tgt_sent if h ==0 else [], ax=axs[h])
plt.show()
print("Decoder Src Layer", layer+1)
fig, axs = plt.subplots(1,4, figsize=(20, 10))
for h in range(4):
draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(sent)],
sent, tgt_sent if h ==0 else [], ax=axs[h])
plt.show()
Encoder Layer 2
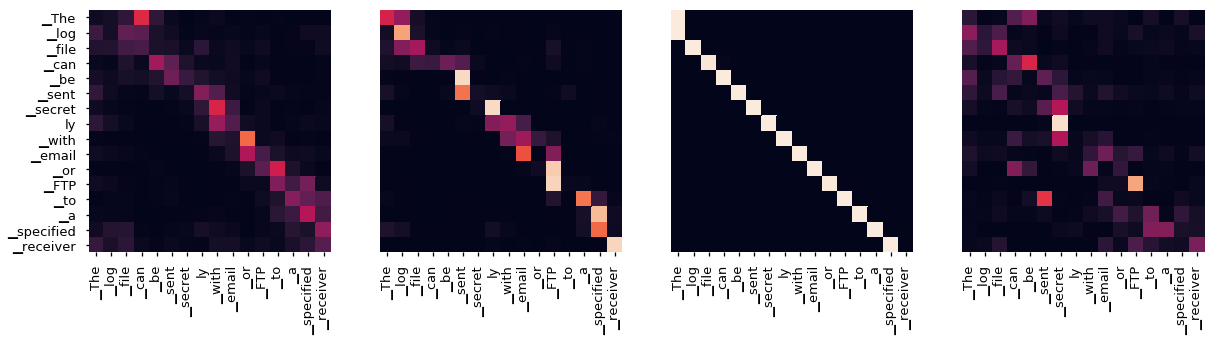
Encoder Layer 4
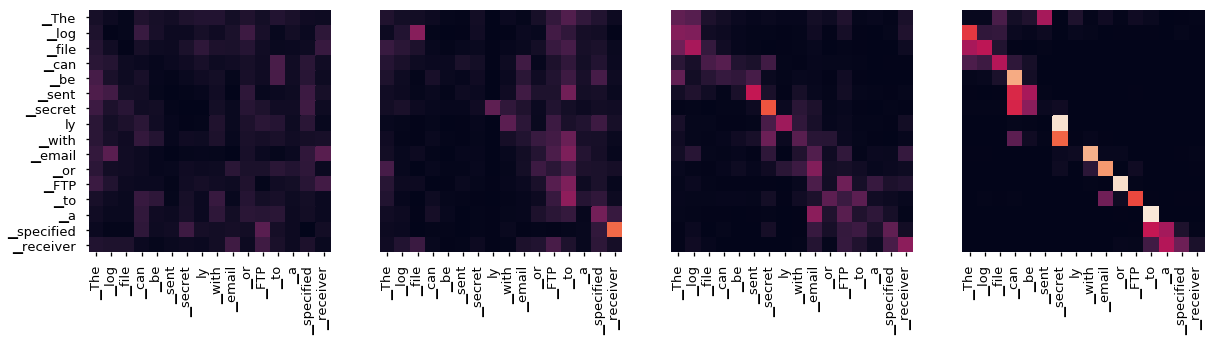
Encoder Layer 6
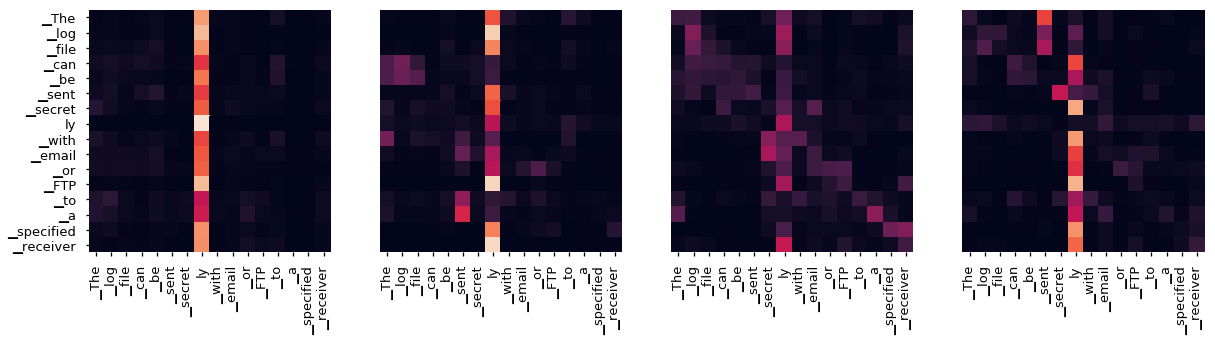
Decoder Self Layer 2
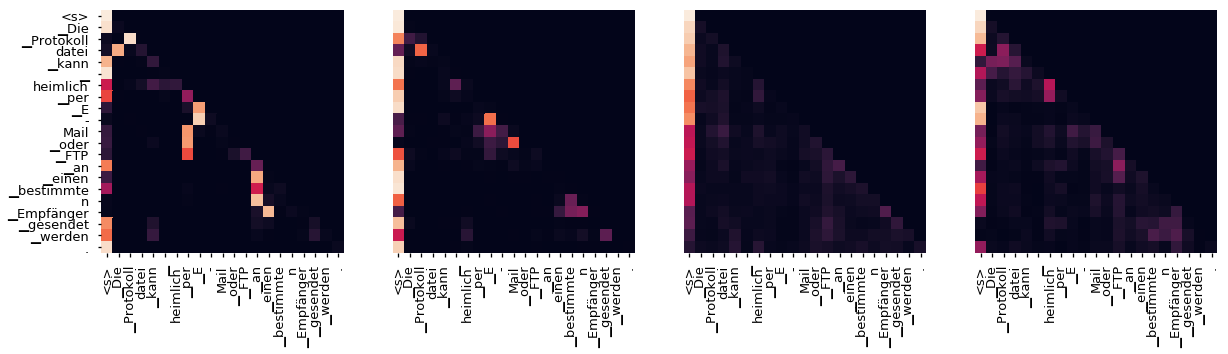
Decoder Src Layer 2
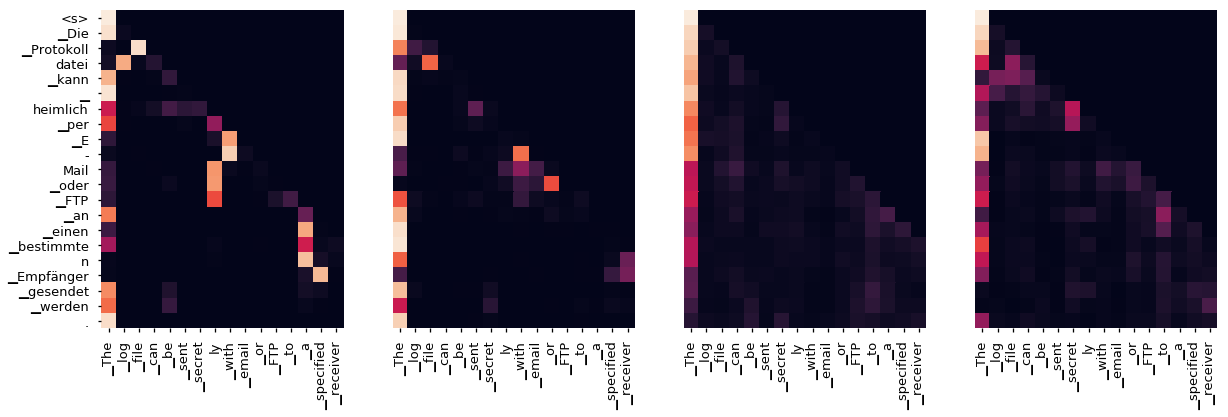
Decoder Self Layer 4
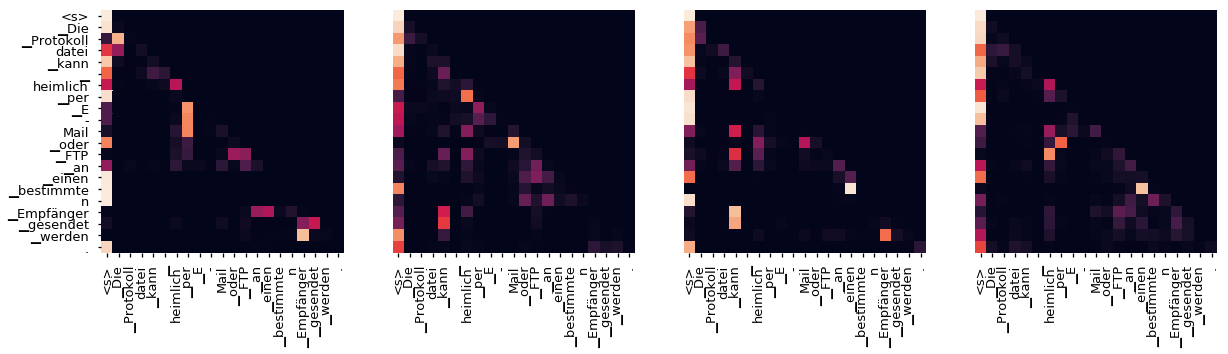
Decoder Src Layer 4
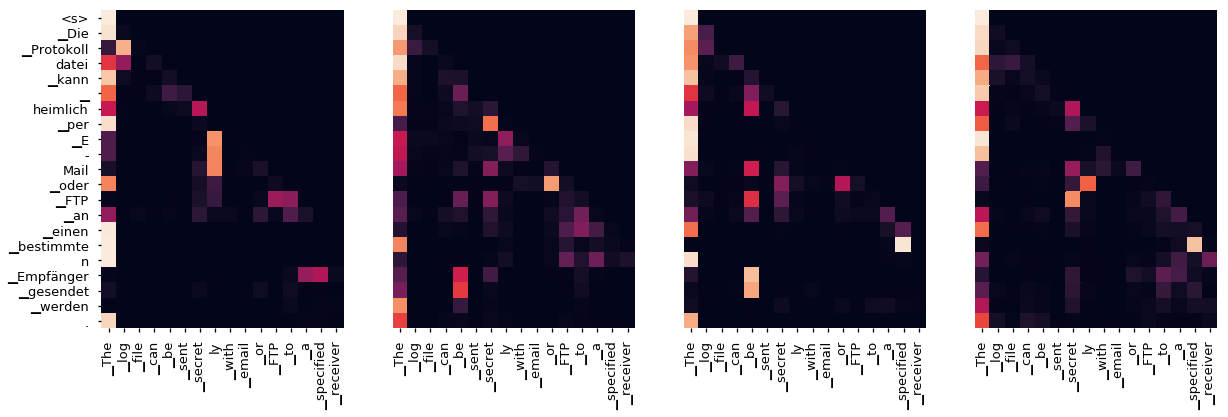
Decoder Self Layer 6
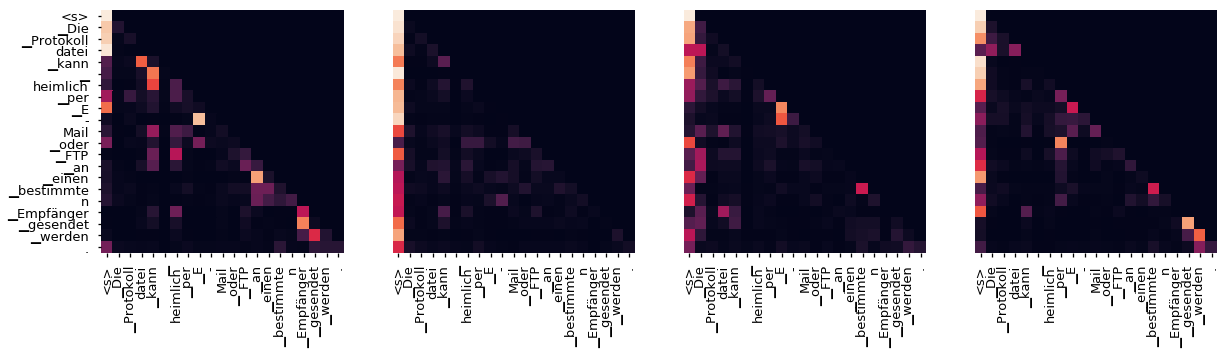
Decoder Src Layer 6
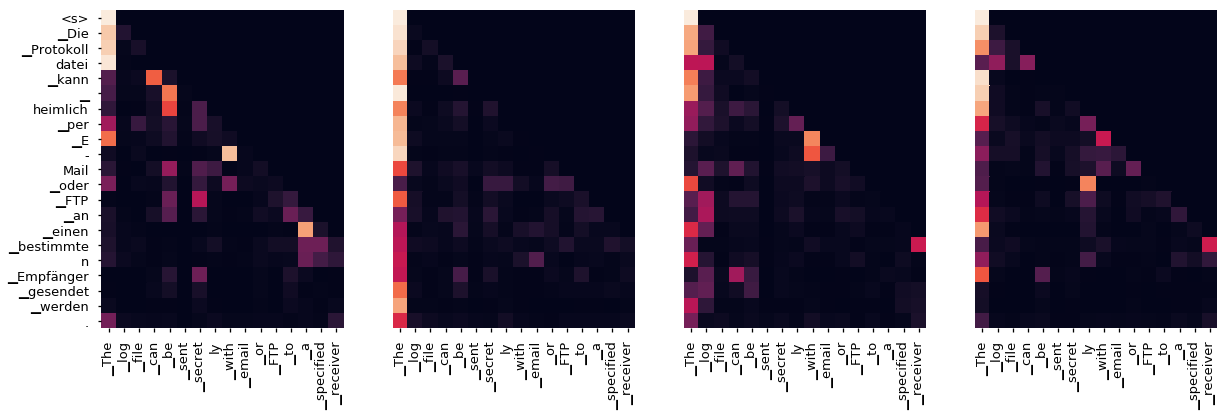
总结
希望这段代码对未来的研究有用。如果您有任何问题,请随时联系。如果您觉得这段代码有帮助,也可以查看我们的其他 OpenNMT 工具。
@inproceedings{opennmt,
author = {Guillaume Klein and
Yoon Kim and
Yuntian Deng and
Jean Senellart and
Alexander M. Rush},
title = {OpenNMT: Open-Source Toolkit for Neural Machine Translation},
booktitle = {Proc. ACL},
year = {2017},
url = {https://doi.org/10.18653/v1/P17-4012},
doi = {10.18653/v1/P17-4012}
}
祝好,
srush
相关资源推荐