电路分析方法对比与实战：支路电流、叠加定理、网孔与节点法详解

电路分析是电子工程的基础，掌握多种分析方法至关重要。常用的方法包括支路电流法、叠加定理、网孔分析法、结点分析法以及戴维南和诺顿定理等。针对不同电路结构和求解需求，灵活选用合适的方法，能显著提升分析效率与准确性。本文将通过具体实例，对上述几种核心方法进行比较与剖析。

支路电流法

支路电流法直接以各支路电流作为求解变量，依次应用基尔霍夫电流定律（KCL）和电压定律（KVL）列出方程组，是电路分析中最直接的方法之一。

分析步骤：

1. 设定各支路电流的参考方向，并为每个独立回路选定绕行方向。对于一个具有 n 个节点的电路，可列出 (n-1) 个独立的KCL方程。
2. 若电路有 m 条支路，则需补充 (m-n+1) 个独立的KVL方程。为简化计算，通常选择网孔（即平面电路内部不包含其他支路的回路）来列写电压方程。对于平面电路，独立的KVL方程数正好等于网孔数。
3. 联立方程组，求解各支路电流。

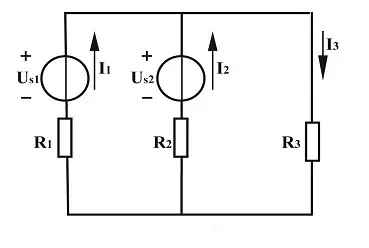
【实例1】 如图所示汽车发电机（Us1=12V）、蓄电池（Us2=6V）与负载（R3=5Ω）的并联电路，其中R1=R2=1Ω。求各支路电流。
分析：支路数 m=3，节点数 n=2，网孔数为2。需设定三个电流参考方向（如图），并选取顺时针为回路绕行方向。
解：

1. 列KCL方程（独立节点 a）：
   I1 + I2 = I3
2. 列KVL方程（网孔1和网孔2）：
   网孔1：I1*R1 - I2*R2 = Us1 - Us2
   网孔2：I2*R2 + I3*R3 = Us2
3. 代入数值求解得：
   I1 = 3.8A, I2 = -2.2A, I3 = 1.6A

叠加定理

叠加定理是线性电路的基本属性。它指出，在有多个独立电源的线性电路中，任一支路的响应（电压或电流）等于各独立电源单独作用时，在该支路产生响应的代数和。这为分析多电源电路提供了清晰的思路，尤其在处理复杂网络/系统时非常有用。

应用要点：

1. “除源”原则：考虑某一电源单独作用时，其它独立电压源应短路（电动势为零），独立电流源应开路（电流为零）。电源内阻（若有）需保留，受控源也应保留在电路中。
2. 方向与符号：各分响应的参考方向应与原电路总响应的参考方向一致。叠加时，方向一致的分量取正，相反则取负。
3. 适用范围：仅适用于计算线性电路的电压和电流，不能直接用于计算功率（功率与电压/电流为平方关系，非线性）。
4. 受控源处理：受控源不能作为独立源参与叠加，应始终保留在电路中。

【实例2】 使用叠加定理求解下图电路中的电流 I3。

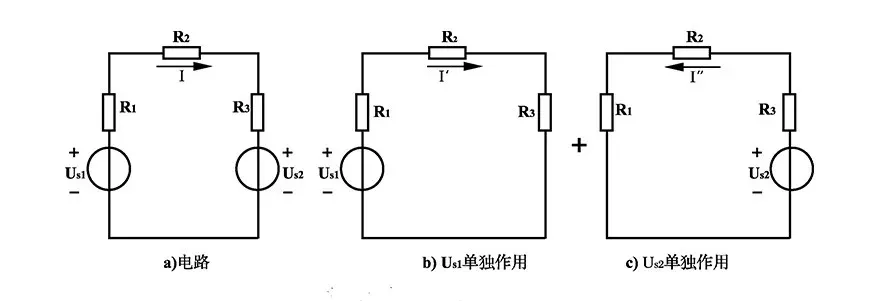
解：将原电路（图a）分解为 Us1 单独作用（图b）和 Us2 单独作用（图c）的叠加。

1. Us1 单独作用时电路：
   
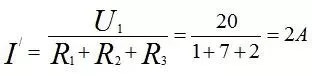2. Us2 单独作用时电路：
   
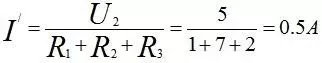3. 由叠加定理，总电流 I3 = I3' + I3''：
   

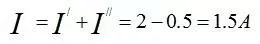
网孔分析法

网孔分析法以假想的网孔电流为求解变量，对每个网孔列写KVL方程。这种方法自动满足了KCL，减少了方程数量，尤其适合网孔数较少的平面电路。

应用要点：

1. 视察法列方程：熟练掌握网孔自电阻、互电阻及等效电压源的概念后，可直接观察电路列出标准形式的网孔方程。
2. 含受控源电路：先将受控电压源视为独立源列写方程，再用网孔电流表示其控制量，然后代入方程整理。

【实例3】 对下图电路列写网孔方程。

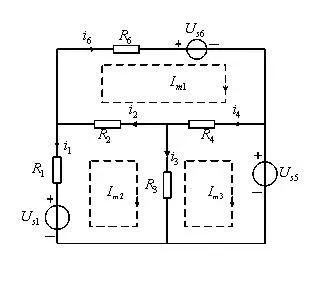
解：设定三个网孔电流 Im1, Im2, Im3 及其参考方向（如图）。首先用支路电流表示各网孔的KVL方程：

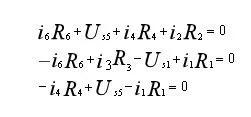
再用网孔电流表示各支路电流：

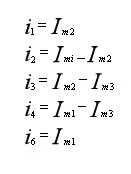
代入KVL方程，整理得到标准的网孔电流方程：

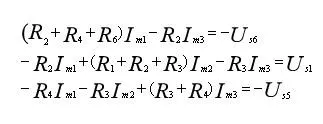
结点分析法

结点分析法以结点电位（电压）为待求变量。选取一个参考结点后，对其余每个独立结点列写KCL方程，并将方程中的支路电流用结点电位表示。该方法在结点数少、支路数多的电路中优势明显。

列写步骤：

1. 选定参考结点，标定其余 (n-1) 个独立结点的电位。
2. 对每个独立结点列写KCL方程，方程中的电流用结点电位差与电导表示。
3. 求解方程组，得到各结点电位。
4. 利用结点电位进一步求解其他电路变量，如支路电流、功率等。

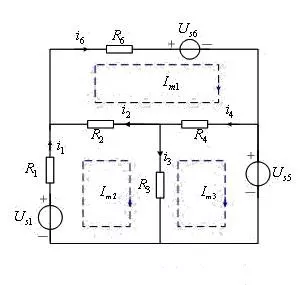
【实例4】 对如图所示电路列写结点方程。
解：设结点④为参考结点，独立结点①、②、③的电位分别为 Un1, Un2, Un3。列写各结点的KCL方程：

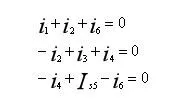
用结点电位表示各支路电流：

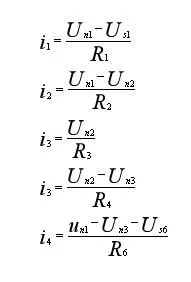
将上述关系代入KCL方程，整理得到简洁的结点电位方程：

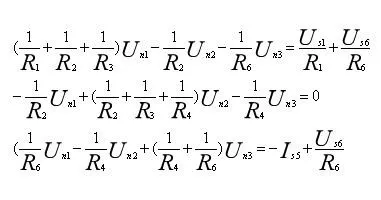
戴维宁定理与诺顿定理

这两个定理用于将复杂的线性有源二端网络等效为一个简单的电压源串联电阻（戴维宁等效）或电流源并联电阻（诺顿等效）电路。特别适用于求解网络中某一特定支路的响应，或分析某个元件参数变化时的影响。

应用步骤：

1. 将待求支路从原网络中移开，剩余部分即为一个有源二端网络。
2. 求开路电压 Uoc：计算该二端网络端口处的开路电压（戴维宁等效电路参数）。
3. 求短路电流 Isc：计算该二端网络端口处的短路电流（诺顿等效电路参数）。
4. 求等效电阻 Req：令网络内所有独立源为零（电压源短路，电流源开路），计算端口处的输入电阻。
5. 用得到的戴维宁或诺顿等效电路替代原二端网络，与待求支路连接，从而简化分析。

【实例5】 如图所示电路，已知电流 I=2A，试确定电阻 R 的值。

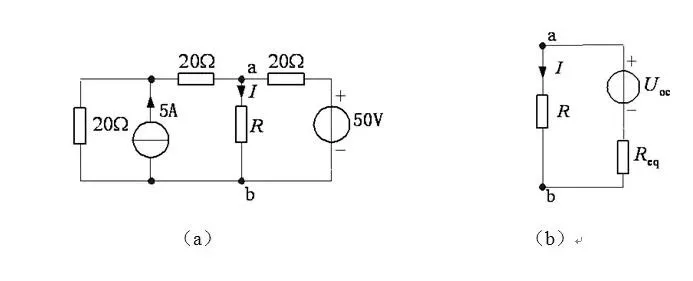
解：先求R左侧电路的戴维宁等效电路（如图b）。

1. 求开路电压 Uoc：运用叠加定理。
   
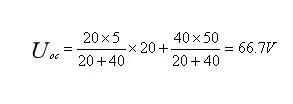
2. 求等效电阻 Req：将所有独立源置零。
   
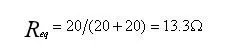
3. 由图b等效电路，根据欧姆定律：
   
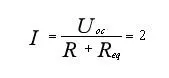
   代入 I=2A 求解得：
   

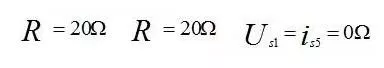
各种方法比较与选用原则

实际电路分析中，往往需要根据电路特点综合运用多种方法。合理选择方法能极大简化计算过程。

• 支路电流法：直接但方程数多（等于支路数），适用于支路不多的电路或利用计算机求解。
• 网孔分析法：以网孔电流为变量，减少了方程数（等于网孔数），非常适合平面电路且网孔较少的情况。它本质上是通过减少变量来提升算法求解效率的思路。
• 结点分析法：以结点电位为变量，方程数等于独立结点数。对于结点少、支路多或非平面电路尤为有效，是电路仿真软件中最常用的方法。
• 叠加定理：适用于线性电路，尤其当多个电源单独作用时的电路更易分析的情况。它是理解线性系统特性的重要工具。
• 戴维宁/诺顿定理：专用于简化局部网络，完美解决“只求某一支路响应”或“分析参数变化影响”这类问题。

总结：对于简单电路，任选一种方法即可。对于复杂电路，需观察其结构特点：支路多但节点少可考虑结点法；网孔少则用网孔法；若只关心单一元件，戴维宁定理往往是捷径。深刻理解每种方法的原理和适用场景，是高效、准确进行电路分析的关键。