Flash-Attention原理与演进详解：从算法优化到硬件加速

为什么不需要缓存 Q？

根据推理阶段的注意力机制计算，由于 Token 1、2、3 在加入计算时都不需要预测未来的信息，所以需要把注意力矩阵右上角的数据（即未来信息）全部掩蔽掉。下面是 3 个 Token 同时输入模型进行推理时的注意力计算情况。

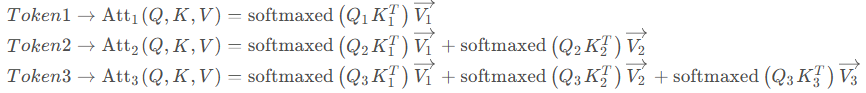
这是其理论计算公式。

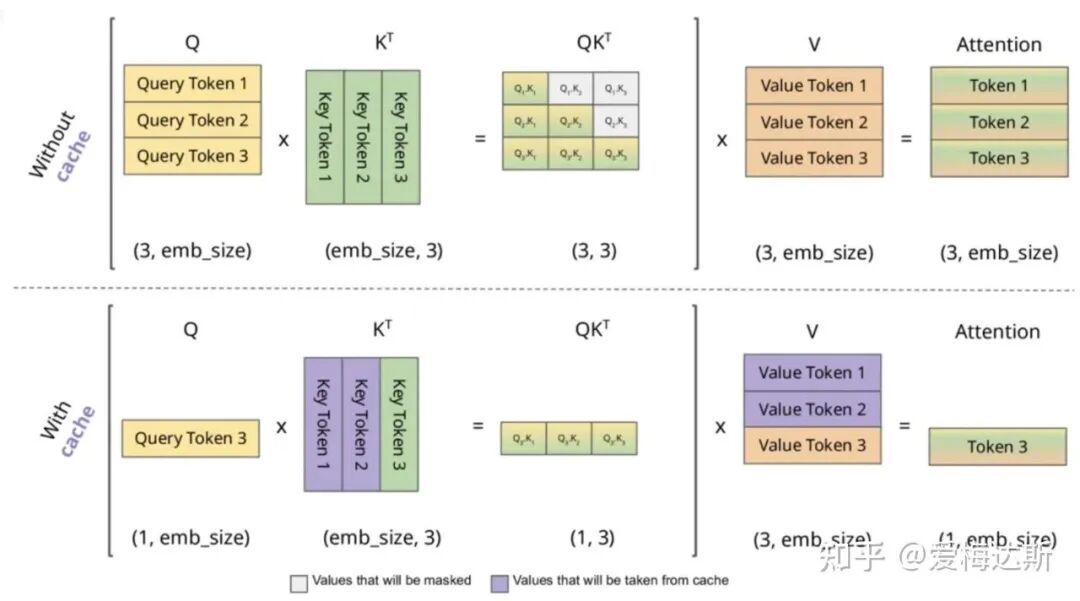
上图展示了实际计算过程的图解。可以看到，在推理时使用 KV Cache 可以避免重复计算历史 Token 的 Key 和 Value，但每个新 Token 的 Query 仍需与所有历史及当前的 Key 进行计算。这正是 Transformer 架构自回归推理的核心模式。

Flash-Attention

由于 KV Cache 在每个注意力层中都会存在，如果按照原始方式计算，那么每次生成新 Token 时都需要从显存中读取整个 KV 历史，这会造成大量的内存访问开销。为了减少高带宽内存（HBM）的访问次数，从而提升计算效率，Flash-Attention 应运而生。

这项工作主要围绕硬件特性进行优化，因此更像是一种底层算子的优化，而非算法层面的改变。

核心挑战：Softmax 的分块计算

对于 Q、K、V 矩阵的乘法计算，初始实现是使用整个矩阵进行运算。由于硬件（如GPU的流处理器）能够同时处理的矩阵块大小有限，为了充分利用硬件并行性，需要对大矩阵进行分块，然后分发给多个处理器单元进行并行计算。

矩阵分块计算完成后，将结果集中相加即可。然而，Softmax 操作却不太容易分块计算。Softmax 分块的主要难点在于它是一个全局规约操作：计算每个元素时需要知道整个向量（或行的）最大值和总和，以防止数值溢出。

Softmax 计算时需要先将输入 x 减去 max(x)，这是因为计算机在计算 e^x 时，当 x 超过一定值（例如 89）就会发生浮点数溢出。标准的 Softmax 公式如下，其中 d 为向量维度：

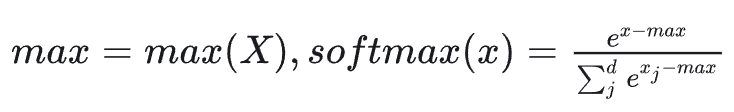
分块Softmax的解决思路

Flash-Attention 的解决思路非常巧妙：它允许先对每个数据块独立进行“局部”的类 Softmax 计算，并记录下该块的统计量（局部最大值和指数和）。待所有块处理完毕后，再通过这些统计量计算出“全局”的最大值和总和，并据此修正每个块的中间结果，最终得到与整体计算完全一致的结果。

让我们通过一个具体例子来理解这个过程。假设有一个向量 X：

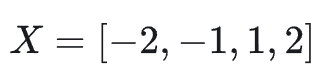
将其分成两块：

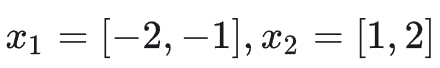
让它们在不同的计算核上并行处理。对于第一块 x1，计算其局部统计量：

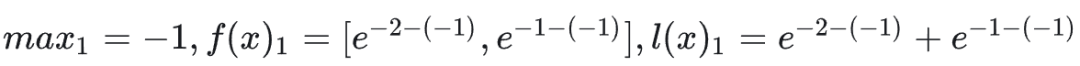
对于第二块 x2，进行类似计算：

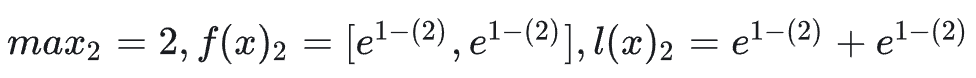
现在，我们需要合并这两块的结果，计算出全局的 Softmax。首先找到全局最大值 max_all，然后根据局部统计量修正得到全局的未归一化结果 f(x)_all 和全局分母 l(x)_all：

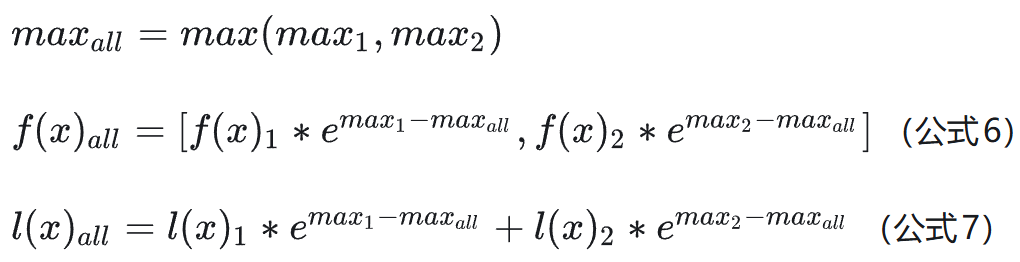
最终，将 f(x)_all 除以 l(x)_all 就得到了全局正确的 Softmax 结果。展开公式 6 和 7 可以发现，其本质就是用全局最大值 max_all 替换了各个局部计算中的局部最大值，并通过指数缩放因子（如 e^{max_1 - max_all}）对局部结果进行修正。这一方法在保证数值稳定的前提下，完美实现了 Softmax 的并行分块计算。

Flash-Attention 1 算法

上述思想被系统化地应用在了注意力计算中。Flash-Attention 1 的完整算法如下，它通过精细的分块和对 HBM 与 SRAM 之间的数据调度，显著减少了内存读写次数：

算法的核心在于外循环遍历 K、V 的块，内循环遍历 Q 的块。在芯片上计算注意力分数 S_ij 后，不是直接写回庞大的中间矩阵，而是立即进行局部 Softmax 统计（计算行最大值 m_ij 和指数和 l_ij），并与之前块的统计量（m_i, l_i）进行在线合并。输出 O_i 也会被增量更新。整个过程只需将最终的 O 写回 HBM，避免了存储中间注意力矩阵（大小为 N x N）的巨大开销。

原论文给出了一个具体的计算示例来阐明这个过程：

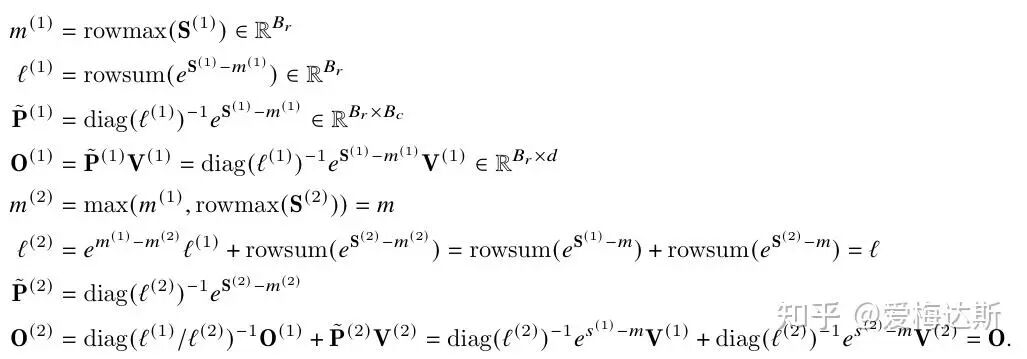
这个示例清晰地展示了如何在分块计算中维护和更新行最大值 m 和归一化分母 l。在得到后续块的全局统计量后，再对之前块的输出进行重新缩放（Rescaling），从而得到一致的结果。这种“在线重归一化”技术是 Flash-Attention 的灵魂。

Flash-Attention 2 的改进

Flash-Attention 2 在版本1的基础上进一步优化，获得了更快的速度。我们可以对比两个版本的核心思想：版本1主要解决了 Softmax 的分块计算问题；版本2则对计算顺序做了更激进的调整，它先计算所有分块的 QK^T V（一个未归一化的中间量），遍历完一行 Q 的所有块之后，再一次性除以全局的归一化分母。

为什么版本2更快？相比于版本1，版本2减少了对分母的重复计算和存储。版本1中，每个块计算后都需要进行一次局部归一化，最后合并时还需再次调整。版本2则推迟了归一化，只需在整行Q处理完毕后做一次除法。这不仅减少了计算量，还节省了存储局部分母和局部最大值的中间内存。

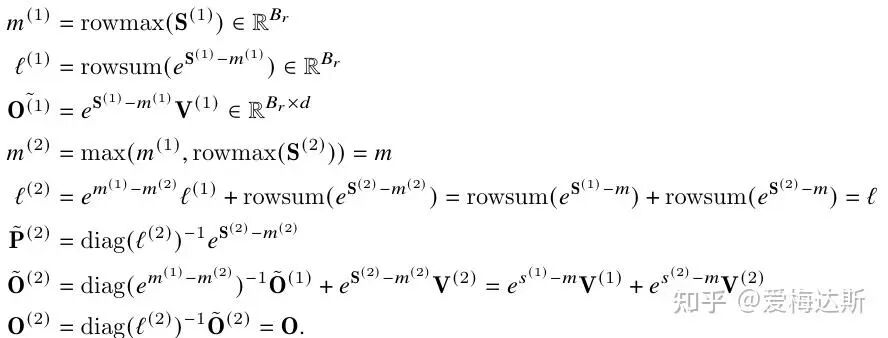
上图为版本2的计算示意。其主要改进点包括：

1. 延迟归一化：注意到最终输出只依赖于全局归一化分母 L。因此，可以将乘法缩放因子的应用推迟到所有块累加完毕之后。两个版本在公式上的关键差异体现在 O^{(2)} 的计算上。
2. 反向传播优化：在反向传播时，版本2只需存储全局的 L 和 m，而不需要像版本1那样存储每个块的中间统计量，进一步节省了内存。
3. 因果掩码的优化：针对自回归语言模型中的因果注意力掩码（Causal Masking），版本2通过调整循环顺序，在计算时直接跳过无效区域（即列索引大于行索引的部分），避免了为未来Token进行计算，显著减少了计算量。这类针对计算模式的优化是 算法 层面的重要实践。

Flash-Attention 3 与硬件协同

Flash-Attention 3 主要针对 NVIDIA H100 等新一代 GPU 架构进行了深度优化，充分利用了新的硬件特性：

• 异步流水线：利用张量核心（Tensor Cores）和 Tensor Memory Accelerator (TMA) 的异步特性，实现数据搬运与计算的流水线并行，掩盖内存延迟。
• 计算重叠：在计算 Softmax 的同时，安排其他的矩阵乘法（如 WGMMA）操作，提高硬件利用率。
• 数据布局适配：解决 FP32 累加器和 FP8 操作数矩阵在内存布局上的不一致性问题，确保数据高效流通。

这一版本的优化标志着性能提升进入了与硬件微架构深度绑定的阶段，对 计算机基础 知识尤其是体系结构理解的要求更高。

本文基于技术分享整理，旨在解析Flash-Attention的核心思想。更多深度学习与高性能计算的前沿讨论，欢迎关注云栈社区。