为什么GPU与NPU精度存在差异？揭秘大模型训练的底层计算秘密

在 AI 大模型训练与推理的实践中，很多工程师都会遇到一个困惑：同样的 FP16/BF16 计算精度，GPU 和 NPU 跑出来的结果却有偏差；甚至同是 NPU，不同代际产品的计算结果也不完全一致。

这些精度差异是正常现象吗？背后隐藏着哪些技术原理？今天我们就来深入拆解，揭开 AI 芯片计算精度的神秘面纱。

一、浮点数的“数学陷阱”：交换律和结合律失效了？

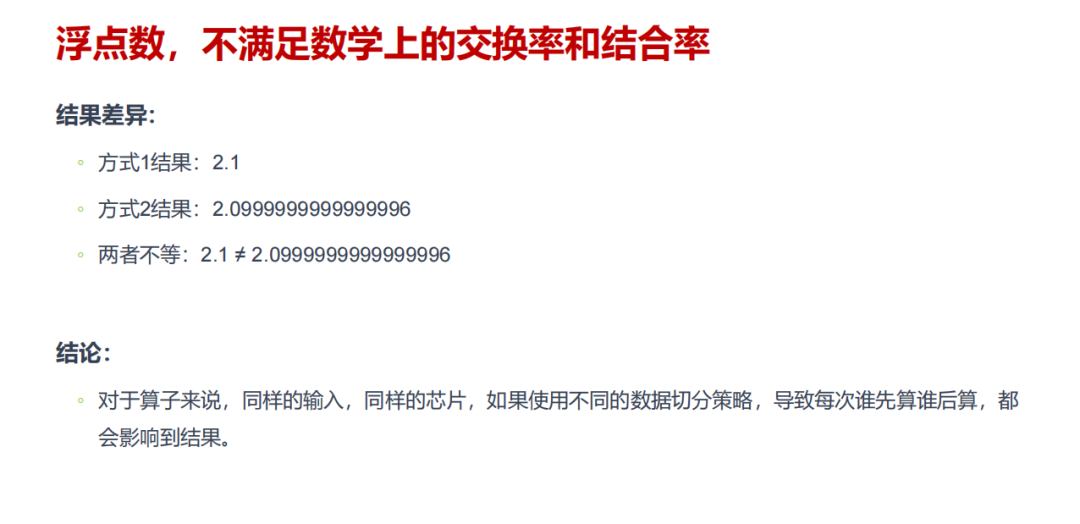
在我们的常识中，加法满足交换律和结合律，1+2+3 和 3+2+1 的结果必然相等。但在 AI 芯片的浮点运算世界里，这个铁律却被打破了。

核心原因是浮点数在计算机中无法被完全精确表示，比如 0.1 在二进制中是无限循环小数，只能近似存储。

而 AI 大模型的计算过程，本质上是海量浮点数的累加与乘法运算。不同芯片的数据流切分策略不同，会导致计算顺序出现差异，进而让浮点误差不断累积，最终呈现出可感知的精度偏差。更关键的是，这种偏差并非芯片质量问题，而是浮点数本身的数学特性所致。

二、硬件底层的“设计分歧”：浮点运算单元各有千秋

如果说浮点数特性是精度差异的“先天因素”，那么硬件实现的差异就是“后天关键变量”。不同厂商的 AI 芯片，在最核心的浮点运算单元（FPU）设计上，从一开始就走上了不同的道路。

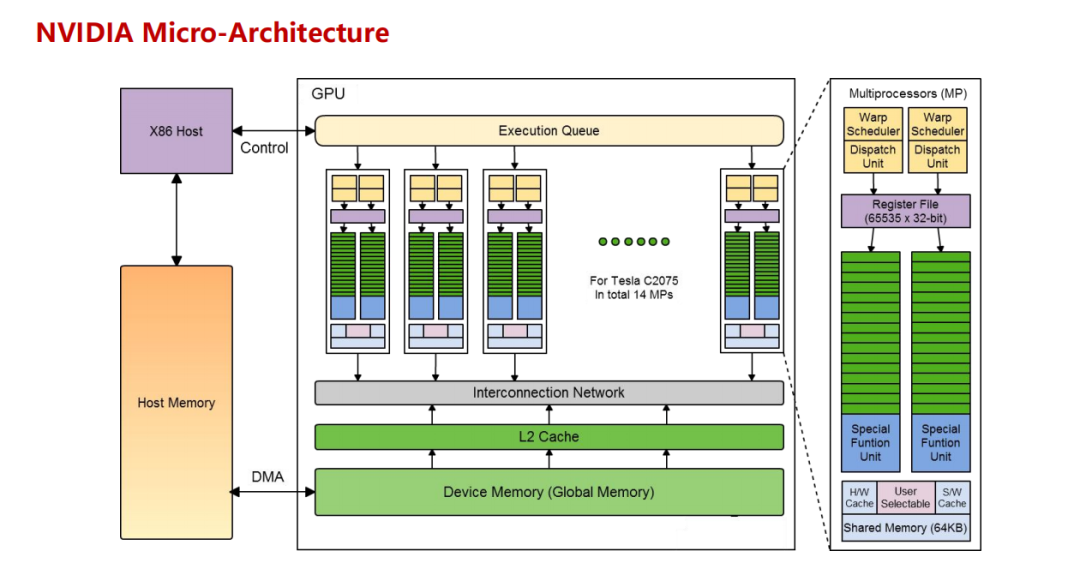
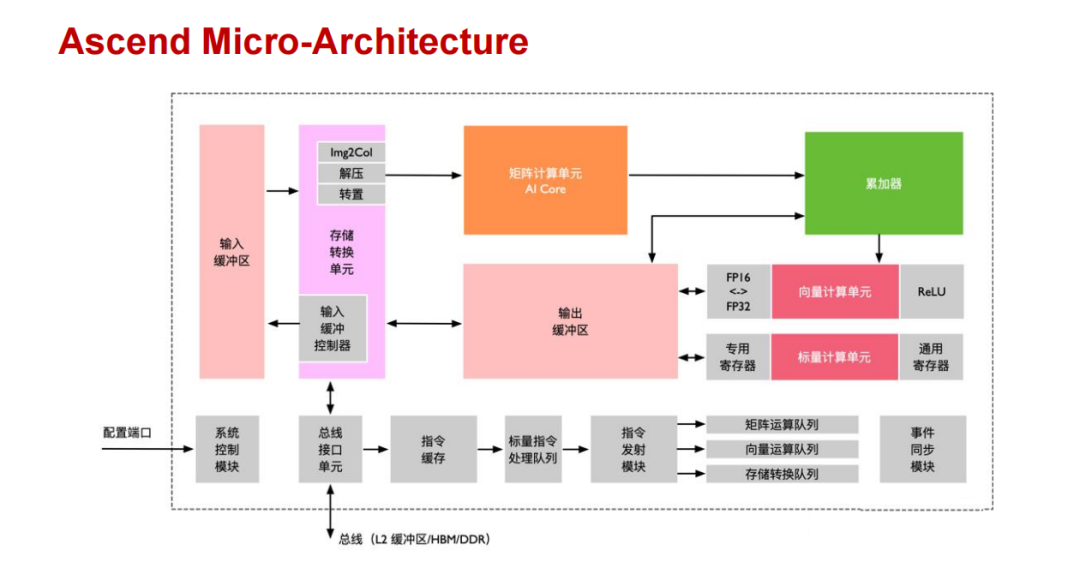
从晶体管级设计来看，NVIDIA 的 GPU 采用了更复杂的累加器结构，其 Tensor Core 专门针对矩阵乘法优化了数据流处理方式；而华为昇腾 NPU 的 Cube Core 则聚焦 AI 场景的矩阵运算，设计了专属计算路径。两者虽然都能高效完成矩阵乘法，但累加器位宽、数据处理逻辑的差异，会直接导致计算结果的细微偏差。

此外，为了提升运算性能，不同芯片对低精度计算（如 FP16）中的非规格化数会采取不同的截断策略。有些芯片会直接截断非规格化数以加快运算速度，有些则会保留更多精度，这种优化策略的分歧，也让精度差异成为必然。

值得注意的是，即便同类型芯片，不同代际产品的精度也会不同。比如 GPU A100 与 H100、NPU A1 与 A2，随着架构升级和硬件优化，浮点运算的实现细节会不断调整，精度自然也会有所区别。

三、软件栈的“底层博弈”：算法与编译器的隐形影响

除了硬件，软件栈的实现差异同样在悄悄改变计算结果。AI 芯片的运算能力需要通过底层数学库和编译器来释放，而不同厂商的实现逻辑差异显著。

在数学库层面，NVIDIA 的 cuBLAS 和昇腾的 CANN 算子库，在矩阵乘法的分块策略、循环展开方式、内存访问优化上都存在不同。以矩阵乘法（GEMM）为例，不同库的分块大小会影响浮点累加的顺序，导致舍入误差的积累方向出现偏差，最终反映在结果上。

编译器的优化则是另一个关键因素。编译器会根据硬件特性对指令进行重排，还会决定是否使用融合乘加（FMA）指令。NVIDIA 的 NVCC 编译器和昇腾 CANN 的底层编译器，生成的指令序列完全不同，这些看似微小的差异，在海量运算中会被不断放大，最终形成可观测的精度差。这背后涉及的计算架构与软件生态协同，是影响最终精度的关键一环。

四、并行计算的“不确定性”：线程与内存的协同难题

大模型训练依赖大规模并行计算，而并行架构本身就存在的非确定性，也会加剧精度差异。

在线程调度层面，GPU 的 CUDA 多线程 warp 调度策略，与昇腾 NPU 的多进程核函数调度方式不同，线程块的执行顺序无法完全固定。这种非确定性会导致浮点运算的累加顺序随机变化，误差积累的路径也随之改变，最终结果自然难以完全一致。

同时，共享内存或缓存（如 L1、L2 缓存）的访问竞争，也会带来精度影响。不同芯片的内存一致性模型不同，数据更新的时序存在差异，尤其是在多线程同时访问同一内存地址时，这种时序差异会间接导致计算结果的微小偏差。

五、误差累积的“蝴蝶效应”：海量运算下的精度放大

大模型的训练过程包含数十亿甚至上万亿次浮点运算，每一次运算引入的微小舍入误差，都会在后续计算中不断累积，最终形成“蝴蝶效应”。

根据 IEEE 754 浮点运算标准，所有芯片都采用“就近舍入”模式处理运算结果，但不同芯片的舍入实现细节存在细微差异。在单次运算中，这种差异可能只有小数点后十几位的偏差，但经过万亿次运算累积后，偏差会被不断放大，最终达到可观测的程度。

不过值得庆幸的是，大模型具有极强的泛化能力，这些微小的精度差异并不会影响模型的整体性能。实践证明，只要将误差控制在小数千分位之后（如双千分之一的误差范围），模型的推理效果和训练收敛速度都不会受到明显影响。

文章总结：精度差异不可怕，可控才是关键

看完这些分析，我们可以得出一个明确结论：GPU 与 NPU 之间、甚至同类型芯片的不同代际之间，计算精度存在差异是必然现象，这是浮点数特性、硬件设计、软件实现、并行架构等多重因素共同作用的结果。

但这并不意味着我们要容忍无限制的精度偏差。在实际应用中，工程师更需要关注的是误差是否可控、是否在合理范围之内。目前行业内已经形成共识，只要将精度差异控制在小数千分位之后，就不会影响大模型的实际使用效果。

对于 AI 从业者来说，理解精度差异的底层逻辑，不仅能帮助我们正确看待计算结果的微小偏差，更能指导我们在芯片选型、模型优化时做出更合理的决策。毕竟在大模型的落地实践中，精度可控比绝对一致更具实际意义。