干货 | 基于PPO强化学习的对冲基金策略动态选择框架实战

在对冲基金管理中，如何动态选择最优交易策略是最大化收益与规避风险的核心难题。传统的模型往往难以适应市场的非平稳性和噪声干扰，导致其预测能力在实际交易中大幅下降。本文提出了一种创新性解决方案：将强化学习（Reinforcement Learning, RL），特别是近端策略优化（Proximal Policy Optimization， PPO）算法，与策略选择过程深度融合。

与直接预测资产价格的模型不同，这个框架的智能体（Agent）并不交易单一资产，而是学习如何在一系列预定义的基础交易策略（如均值回归、动量策略）之间进行自适应切换。通过利用RL的试错与反馈机制，算法能够在满足风险约束的前提下，动态优化其策略配置，从而最大化风险调整后的累积回报。虽然训练这样的交易智能体需要消耗大量的计算资源，但我们的回测结果证实，这种方法为对冲基金的策略管理开辟了新的、高效的途径。

引言

对冲基金管理的核心在于，如何根据瞬息万变的市场条件，动态地选择并切换交易策略。传统方法在处理市场的非平稳性和复杂数据结构时常常力不从心，导致模型在样本外数据甚至实盘交易中表现不佳。尽管机器学习和强化学习已被广泛应用于高频交易、做市和投资组合管理等领域，但许多现有的RL交易智能体往往缺乏对金融市场先验知识的理解，难以有效分解和分析驱动收益的风险因子（Risk Factors）。

针对以上痛点，本研究设计并实现了一个基于PPO的算法框架，专门用于优化对冲基金管理和资产交易中的策略选择。这个智能体不直接输出买卖信号，而是输出对交易策略的选择，这相当于对损益（PnL）结构进行中长期的管理决策。该算法旨在生成一条贯穿整个非平稳市场轨迹的最优策略路径，不仅关注利润，更将风险作为决策过程的核心考量。

文献综述

算法交易在金融市场已十分普及，对冲基金更是其深度应用者。目前的研究大多聚焦于开发基于深度学习或RL的单一资产价格预测模型或交易执行算法。例如，有研究利用TD3算法进行连续动作空间的股票交易，或使用LSTM网络预测股价走势。然而，许多现有方案过分追求利润最大化，忽视了至关重要的风险因素，同时模型的可解释性与鲁棒性也依然是悬而未决的挑战。

当前研究存在一个明显的空白：多数深度强化学习模型致力于解决“买卖什么资产”的问题，却较少触及“选择何种策略”这一更高层次的管理决策问题。此外，关于如何分解PnL结构并将其用于指导机器学习算法的研究也意义重大。本文的工作正旨在填补这一空白——我们构建了一个可扩展的框架，利用RL在动量与均值回归等基础策略之间进行动态调度，从而系统性地优化风险调整后收益。

方法论

数学模型

我们将策略选择问题形式化为一个部分可观测马尔可夫决策过程（POMDP），用一个七元组 <S， A, O， T， R, Z， γ> 表示：

• S (State)：有限状态集合，满足马尔可夫性质。
• A (Action)：有限动作集合。在此场景下，动作空间由策略配置构成，即从基础策略集 {策略1， 策略2， ...} 中选择特定的策略。
• O (Observation)：观测集合。
• T (Transition)：状态转移模型。
• R (Reward)：奖励函数。它可以是简单的收益率，也可以是夏普比率（Sharpe Ratio）、CVaR（条件风险价值）或CDaR（条件在险亏损）等更复杂的风险调整后指标。
• Z (Observation Model)：观测模型。
• γ：折扣因子，取值 [0， 1)。

我们的目标是开发一个策略 π，在满足风险约束的前提下，最大化期望累积回报。

核心概念

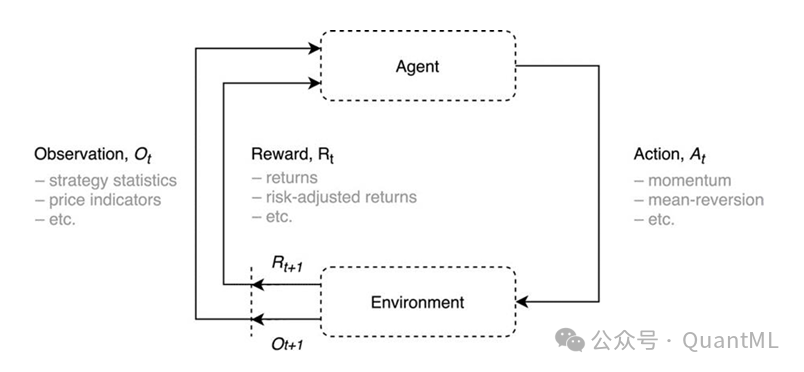
1. 环境（Environment）：指智能体学习所在的动态系统，具体为以FAANG股票为代表的美国股票市场。环境不仅是数据源，还提供了重置状态、执行动作、返回观测值和奖励的接口。
2. 智能体（Agent）：作为控制器，基于当前观测 O_t 选择最优动作 A_t。在本研究中，智能体即是那个选择交易策略的决策者。
3. 动作（Action）：智能体在时间 t 发出的控制信号。具体任务是在动量策略与均值回归策略之间进行切换。
4. 状态（State）：智能体的内部状态 S_t 是环境当前状态 S_t^env 的函数。由于金融市场不可能完全可观测，智能体依赖于观测序列 O_0， A_0, R_0, O_1， A_1, R_1, ...（包含历史观测、动作和奖励）。状态不仅包含价格数据，还可纳入基本面数据、市场情绪指标以及期权链等衍生数据。
5. 策略（Policy）：函数 π，用于描述智能体的行为。随机策略 π(a|s) 表示在状态 s 下采取动作 a 的概率分布。
6. 价值函数（Value Function）：
   • 状态价值函数 V^π(s)：评估处于当前状态 s 的长期价值。
   • 动作价值函数 Q^π(s, a)：评估在状态 s 下采取动作 a 的长期价值。

交易策略本质

智能体并非直接交易资产，而是管理一个“策略组合”。本研究选用的两种基准策略基于截然不同的市场异象：

• 动量策略（Momentum）：旨在从价格趋势的持续性中获利。如果过去一段时间回报为正，则买入；反之则卖出。这是一种顺势交易。
• 均值回归策略（Mean-Reversion）：旨在从资产价格回归其长期趋势（均值）的倾向中获利。当价格偏离均值过大时，进行反向操作。

从风险角度看，这两种策略具有不同的“准Gamma风险”。动量策略类似于做多Gamma（追涨杀跌），而均值回归策略类似于做空Gamma（高抛低吸）。将两者智能结合，有望获得优于单一策略或简单的买入持有（Buy-and-Hold， B&H）策略的表现。

绩效指标

我们的评估采用多维度视角，而非依赖单一指标：

1. 累积回报（Cumulative Return）：衡量投资组合价值的百分比总变化。
2. 市场价值（Market Value）：反映多头和空头头寸的总敞口。
3. 回撤（Drawdown）：从资产峰值到谷值的跌幅，用于衡量下行风险。
4. 条件在险亏损（CDaR）：由Chekhlov等人提出的指标，其优势在于评估所有回撤序列的尾部风险，而不仅仅是最大回撤。
5. 条件风险价值（CVaR）：用于量化资产或策略尾部风险的指标，衡量在给定置信水平下的预期损失。
6. 奖励函数（Reward Function）：我们将其定义为特定时期内的夏普比率（Sharpe Ratio）。这意味着智能体的决策质量直接取决于风险调整后的回报，而非单纯的绝对收益额。

算法开发

关键点

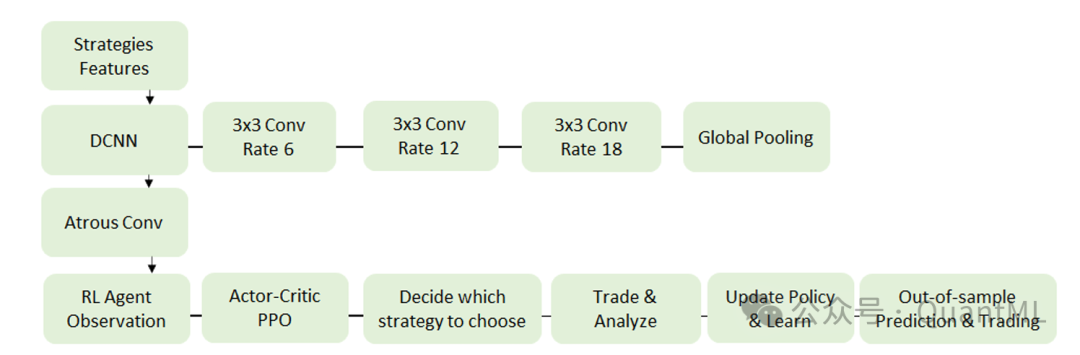
整个交易过程被抽象为一个POMDP。智能体观察系统状态，并决定当前是采用动量策略还是均值回归策略更优。最先进的金融交易需要考虑那些驱动回报的风险因子。资产的预期超额回报通常可被分解为增长因子Beta、通胀因子Beta、流动性因子Beta等。大多数机器学习或强化学习模型难以理解这些风险溢价的结构，容易收敛到通过承担过度尾部风险来换取高夏普比率的危险解。

本模型的核心创新在于不交易单一资产，而是交易一个策略集合。这种方法允许我们操作和扩展大型交易模块，并能在不同的宏观经济背景下，提取和利用不同策略的投资质量。

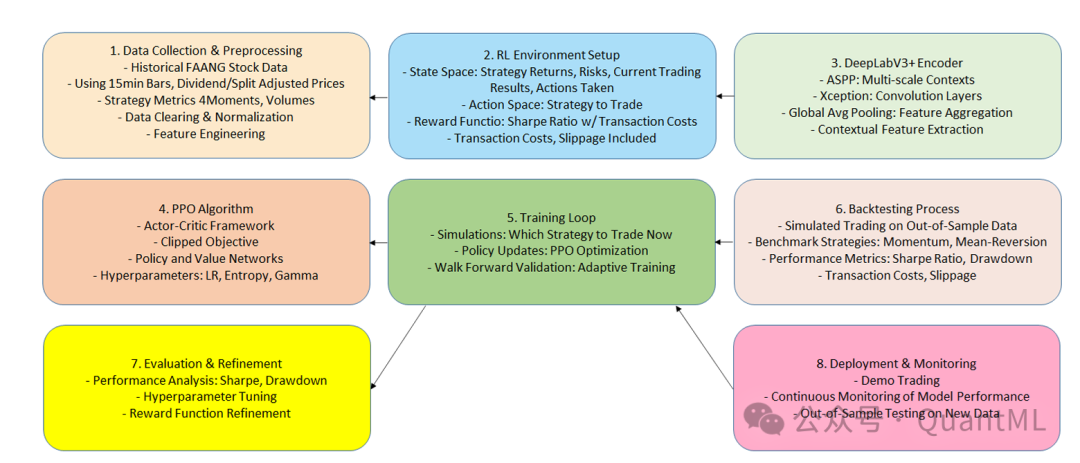
PPO算法

我们选择PPO算法，主要是因为它能有效解决传统策略梯度方法中常见的样本效率低下和训练不稳定问题。

• 核心优势：通过限制更新后策略与旧策略的概率比 r_t(θ) 在 [1-ε， 1+ε] 范围内，防止策略更新步长过大而发生剧烈、有害的变化。
• 目标函数：L_t(θ) = E_t[L_t^{CLIP}(θ) - c_1 L_t^{VF}(θ) + c_2 S[π_θ](s_t)]，这是剪切后的代理目标函数、价值函数损失和熵项的线性组合。熵项 S 用于鼓励智能体进行探索。
• PPO算法实现相对简洁，且其超参数调整较为直观，更适合处理金融时间序列的复杂性。

模型配置与架构

为了从高维市场数据中提取有效特征，本研究基于DeepLabV3+ 编码器架构进行了适应性调整。

• 特征提取：DeepLabV3+ 最初用于计算机视觉的语义分割任务，其核心特点是利用空洞空间金字塔池化（ASPP）。这种结构允许通过不同膨胀率（dilation rate）的扩张卷积层，在不同感受野尺度上编码上下文信息。
• 金融场景适用性：在金融语境下，这意味着模型可以同时捕捉短期市场波动和长期趋势模式。
• 输入：观测空间是一个形状为 (C， H) 的张量，其中 C 是指标数量，H 是历史回看窗口长度。数据包括收益率分布的前四阶矩、成交量等技术指标。
• 动作空间：{0: 动量策略， 1: 均值回归策略}。
• 决策频率：限制在每15分钟K线进行一次决策，允许智能体做出及时的短期调仓判断。
• 验证方法：采用滚动样本外（Rolling Out-of-Sample） 验证。每隔一个固定周期（如一天），模型权重会重置，并仅基于截至当前的最新可用数据重新开始学习。这种方法最接近真实的交易环境，能有效避免前视偏差。

验证与绩效分析

回测方法

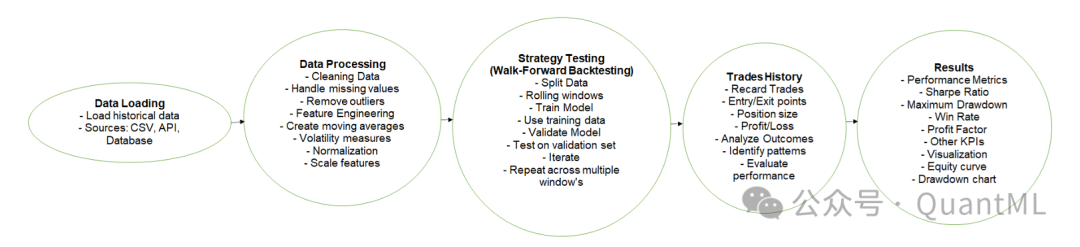
回测是开发和验证任何交易策略不可或缺的阶段。我们使用历史数据来模拟交易，并计算一系列策略绩效统计量。

• 数据清洗与处理：这一步至关重要，需要处理幸存者偏差、数据窥探等问题。
• 交易成本：在回测中，我们明确包含了交易佣金、做空成本以及滑点。滑点被建模为偏离目标执行价格的一个固定百分比。
• 基本假设：我们假设市场有充足的流动性，订单能瞬间执行（T+0），并且智能体的交易行为不会对市场价格产生冲击。

结果分析

我们的回测覆盖了2020年1月1日至2021年8月1日。这一时期包含了因COVID-19引发的市场恐慌性下跌及随后的量化宽松复苏，市场波动性极高，是检验算法适应性的理想样本。

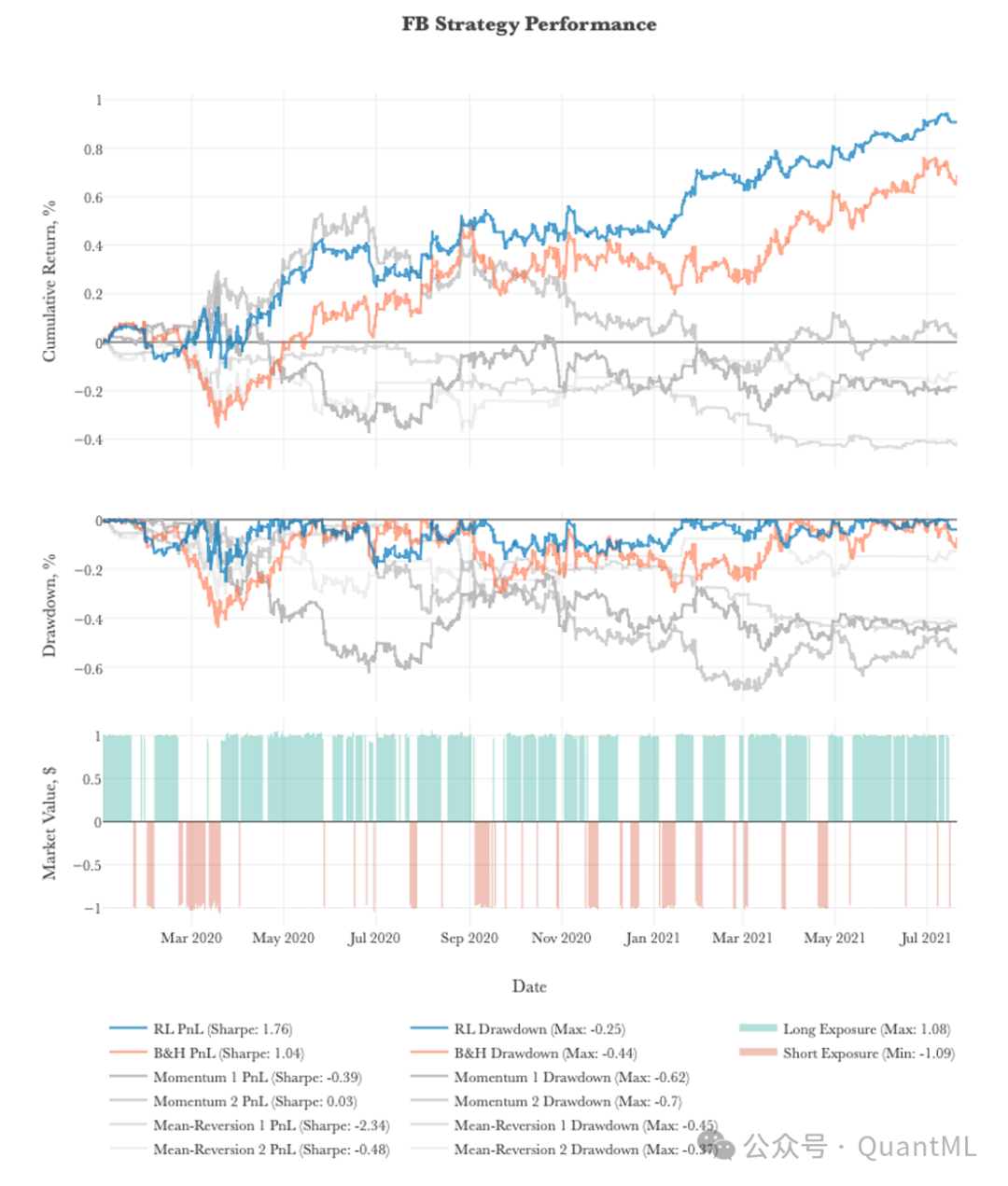
针对FAANG股票（FB， AMZN， AAPL， NFLX， GOOG）的测试结果表明：

1. 综合表现优异：由RL智能体生成的动态策略，在夏普比率、CVaR和CDaR等多个风险调整后指标上，均显著且稳定地优于任何单一的基准策略（动量或均值回归）以及简单的买入持有策略。
2. 夏普比率大幅提升：
   • AAPL：RL策略的夏普比率高达 2.90 ± 0.18，而B&H策略仅为1.37。
   • NFLX：RL策略夏普比率为 2.38 ± 0.13，远超B&H的0.66，也远优于动量或均值回归策略的负值或低正值。
   • FB & AMZN：RL策略同样展现了最高的夏普比率和最低的尾部风险（CDaR）。
3. 强大的环境适应性：RL智能体能够有效推断当前所处的金融环境，并选择当下最有利的策略。即使某个基础策略在测试期的总回报为负，RL智能体依然能通过动态切换，预测其短期生存能力并从中获利。
4. 出色的风险控制：在衡量尾部风险的CVaR和CDaR指标上，RL策略通常表现出更低的风险水平。例如，在FB股票上，RL策略的CDaR为0.17，远低于B&H策略的0.51。

学习过程

通过可视化折扣奖励分布随训练迭代的变化，我们可以清晰地观察到模型的学习过程：

• 初始阶段：奖励分布呈现多峰形态，且概率质量主要集中在左侧（低奖励、负奖励区域）。
• 学习后期：随着PPO算法不断迭代（大约50，000次迭代后），奖励分布整体显著向右侧（正奖励区域）偏移，分布的尾部收缩，多峰性消失。这表明模型成功地学会了区分不同的数据结构，并建立了从观测空间到动作空间的有效映射。

实际应用与局限性

数据与算力需求

• 数据源：我们主要使用了来自Bloomberg的原始金融数据，包括价格、成交量、收益率密度函数统计、波动率估计以及自回归比率等。
• 计算成本：RL算法受限于其较高的计算复杂度。模型训练可能非常耗时且昂贵，需要高性能计算资源支持（本研究使用了配置为16 vCPU， 64 GB RAM的远程服务器）。
• 企业事件处理：正确处理股票拆分、股息支付和并购等公司行为至关重要，需要对其引发的价格跳变进行复权调整，以避免非市场因素误导模型。

当前局限性

1. 黑箱性质：深度强化学习模型普遍缺乏可解释性，其内部决策逻辑难以完全追溯和理解，这影响了在实际投资中的可信度。
2. 对超参数敏感：RL方法的性能高度依赖于策略网络初始化、学习率、熵系数等超参数的精细调优。
3. 回测与实盘的差距：尽管我们采用了滚动样本外测试来模拟真实环境，但历史表现绝不能保证未来结果。实盘交易中可能存在的订单执行延迟、流动性突然枯竭以及市场微观结构变化，都可能导致模型性能出现偏差。

未来方向

• 特征归因与可解释性：建议引入SHAP值、ICE图或PDP图等方法对模型决策进行解释，尝试打开“黑箱”，理解哪些市场特征驱动了策略切换。
• 计算优化：针对GPU计算架构对模型进行进一步适配和优化，以降低训练时间和成本。
• 策略扩展性：该框架可以扩展到包含更多类型的证券（如期货、期权）以及更广泛的基本面因子和另类数据（如新闻情绪分析、社交媒体数据）。

结论

本研究成功构建并验证了一个基于PPO算法的对冲基金策略动态选择框架。通过将动量策略和均值回归策略作为智能体的可选动作空间，该模型能够在非平稳的市场环境中，实现显著优于传统基准方法的、经风险调整后的收益。

核心结论可归纳为以下三点：

1. 有效性：所开发的交易智能体生成的动态策略，在统计意义上显著优于所有基准策略（单一动量、单一均值回归、买入持有）。
2. 环境适应性：得益于DeepLabV3+架构的上下文感知能力，智能体能够有效识别市场机制的状态变化，并相应地调整其策略配置。
3. 内生的风险管理：通过将夏普比率直接设定为奖励函数，模型在优化过程中自然地重视投资组合的PnL结构，从而有效压低了尾部风险（表现为更优的CVaR/CDaR指标）。

尽管面临计算成本高昂和模型可解释性不足等现实挑战，但本研究有力地证实了AI驱动的方法在复杂金融策略管理领域的巨大潜力，为未来的量化投资研究奠定了坚实的基础。未来的工作应聚焦于提高模型决策的透明度、整合更丰富的多因子市场模型，并在更接近真实的交易仿真环境中进行持续验证与迭代。我们也在云栈社区分享了更多关于算法实现与性能优化的技术讨论，欢迎深入交流。