在上一篇探讨图像分类基础方法的基础上,我们知道线性分类器的效果取决于找到一组最佳的权重W。随之而来的关键问题是:如何量化评估这组权重W的好坏?如何衡量模型预测的准确度?这引出了机器学习中至关重要的概念——损失函数(Loss Function)。
一、损失函数:模型性能的量化标尺
损失函数是评估模型预测效果的核心工具,它旨在量化模型预测值与真实标签之间的“差距”或“不满意度”。寻找最佳权重W的过程,本质上就是通过优化算法(如梯度下降)来最小化这个损失函数值的过程。
一个模型的总损失通常由两部分构成:
- 数据损失(Data Loss):衡量模型预测与训练数据真实标签的匹配程度,是所有训练样本损失的平均值。最小化数据损失意味着模型能更好地拟合训练数据。
- 正则化损失(Regularization Loss):用于惩罚模型复杂度,防止过拟合,这是下一篇我们将详细讨论的内容。
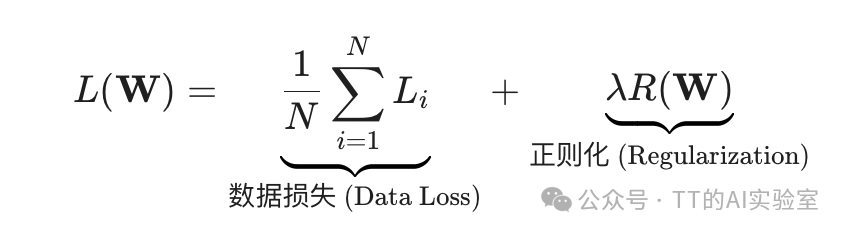
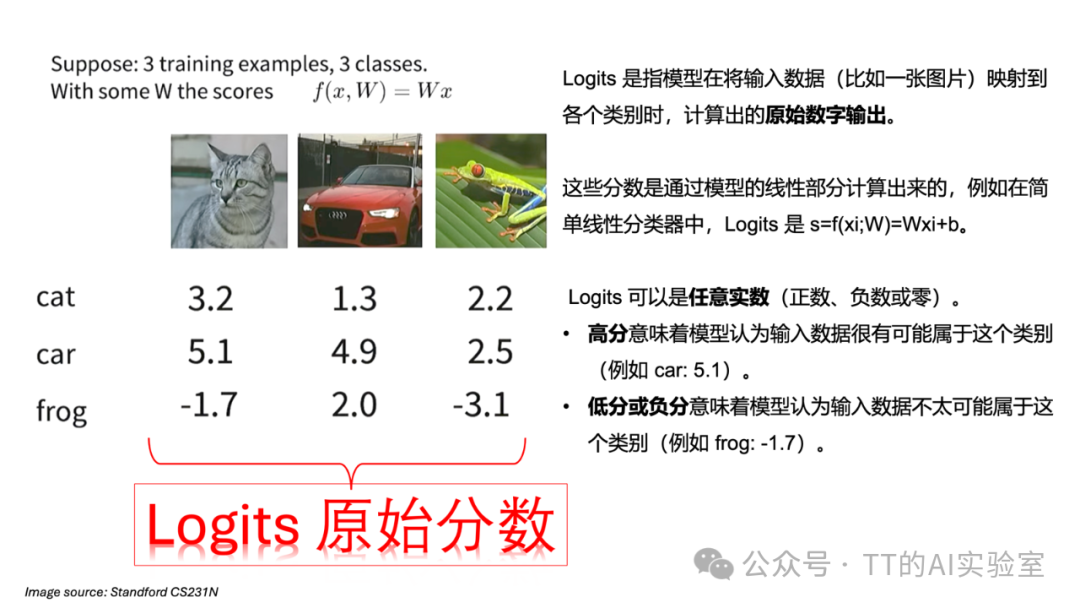
二、Softmax函数:从原始分数到概率分布
为了计算数据损失,我们首先需要将模型输出的原始分数(Logits)转换为直观的概率形式。在分类任务中,最常用的方法是Softmax函数,它属于人工智能领域中处理分类问题的核心数学工具。
Softmax函数的作用是将一组任意实数(Logits)转换为一组总和为1的概率值。这个过程分为三步:
步骤1:输入原始分数(Logits)
模型对输入图像会为每个类别输出一个原始分数,这些分数是未经过归一化的。
步骤2:指数化(Exponentiation)
应用自然指数函数 $e^x$ 对每个原始分数进行转换,得到未归一化的概率。这样做有两个目的:一是确保所有值为正数(概率非负),二是放大分数间的差异,使高分更突出。

这里使用的自然常数 e(约等于2.71828)在数学和人工智能的许多领域中至关重要,因为它描述了连续增长/衰减的极限,且其导数等于自身,这使得后续的梯度计算非常简洁。

步骤3:归一化(Normalization)
将指数化后的每个值除以所有值的总和,从而得到归一化的概率分布,确保所有类别的概率之和为1。
Softmax函数的完整公式为:
$$P(y_i) = \frac{e^{s_i}}{\sum_{j} e^{s_j}}$$

经过Softmax转换后,我们得到了一个清晰的概率分布(例如:87%为车,13%为猫,0%为青蛙),它代表了模型对每个类别的“信心指数”。这个分布符合概率论的公理,具有明确的统计学意义。
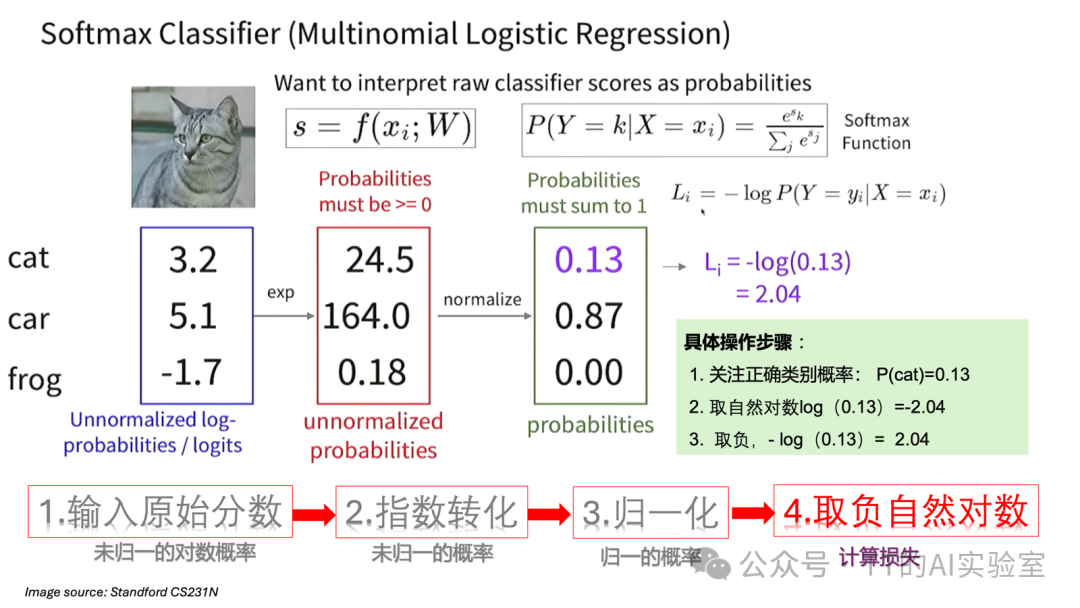
三、Softmax损失(交叉熵损失):衡量预测差距
得到概率分布后,我们需要一个标准来评判它的好坏,即计算损失。Softmax损失函数(也称为交叉熵损失)正是用于此目的。它的目标直白而有力:最大化模型对正确类别的预测概率。
1. Softmax损失公式
对于一个训练样本,其损失 $L_i$ 计算如下:
$$L_i = -\log P(y_i)$$
其中,
$P(y_i)$ 是模型分配给该样本真实类别
$y_i$ 的Softmax概率。
为什么是这个形式?
- 关注正确概率:损失只关心模型对正确答案的信心 $P(y_i)$。$P(y_i)$ 越高,模型越好。
- 引入对数(log):使用自然对数(ln)是出于数学上的便利。首先,它与Softmax中的指数函数 $e$ 互为逆运算,求导简单。其次,在最大似然估计框架下,我们需要最大化所有训练样本预测概率的乘积,取对数后可以将乘积转化为求和,避免数值下溢问题。
- 取负号(-):为了将“最大化对数概率”的目标转化为标准的“最小化损失”问题。当 $P(y_i)$ 接近1(预测完美)时,$-\log(1) = 0$,损失最小;当 $P(y_i)$ 接近0(预测极差)时,$-\log(0) \to +\infty$,损失巨大。
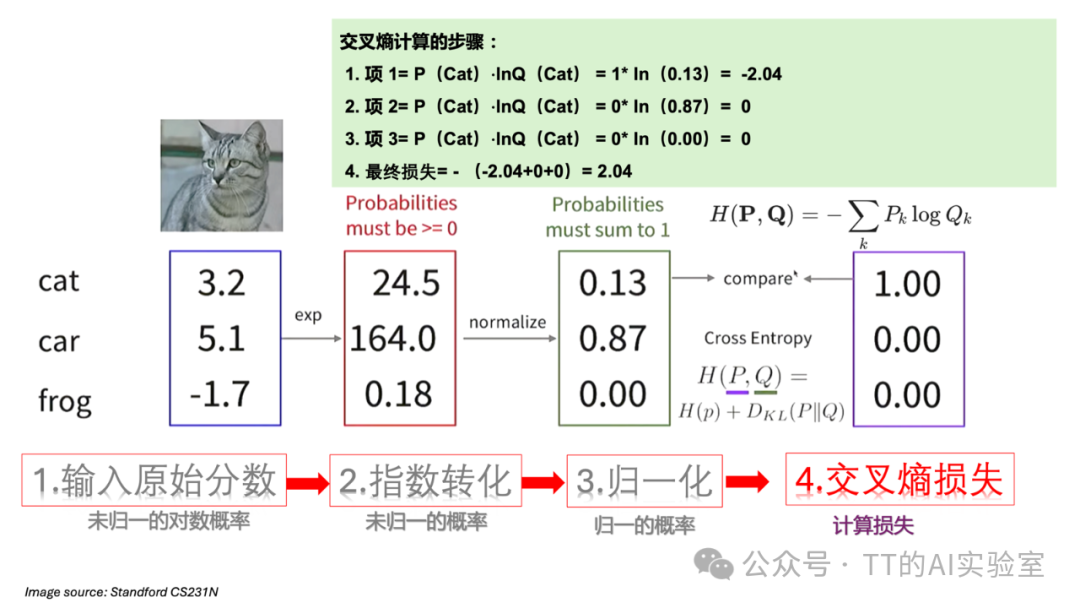
2. 为何也叫交叉熵损失?
从信息论的角度看,交叉熵衡量的是两个概率分布之间的差异。在分类任务中,一个是真实的分布(通常用“独热编码”表示,正确类概率为1,其余为0),另一个是模型预测的Softmax概率分布 $Q$。
交叉熵 $H(P, Q)$ 的公式为:
$$H(P, Q) = -\sum_{x} P(x) \log Q(x)$$
由于真实分布 $P$ 是独热编码,只有正确类别 $y_i$ 处 $P(x)=1$,因此上述公式简化为:
$$H(P, Q) = -1 \cdot \log Q(y_i) = -\log P(y_i)$$
这与Softmax损失公式完全相同。因此,Softmax损失与交叉熵损失在分类问题中是等价的。最小化这个损失,就是在迫使模型预测的概率分布 $Q$ 不断逼近真实的分布 $P$。
四、损失函数的极值与初始值
了解损失函数的范围有助于我们调试模型:
- 理论极值:当模型对正确类别的预测概率 $P \to 1$ 时,损失 $L_i \to 0$(最小值)。当 $P \to 0$ 时,损失 $L_i \to +\infty$(最大值)。
- 初始期望值:在模型权重随机初始化时,对于一个有 $C$ 个类别的任务,每个类别的预测概率大约为 $1/C$。因此,初始损失大约为 $L_i = -\log(1/C) = \log C$。例如,对于10分类任务,初始损失约为 $\ln(10) \approx 2.3$。
小结与展望
本篇深入探讨了损失函数在图像分类中的核心作用,并详细剖析了最常用的Softmax损失(交叉熵损失)。其核心流程是:模型输出Logits -> Softmax函数转为概率分布 -> 通过交叉熵计算损失。这个损失值量化了当前模型参数的“不满意度”,是驱动模型通过梯度下降等人工智能算法进行学习的根本动力。
然而,仅仅最小化数据损失可能会导致模型过度关注训练数据中的细节甚至噪声,从而在新数据上表现不佳,即过拟合(Overfitting)。为了对抗过拟合,我们需要在总损失中加入一个额外的部分——正则化项(Regularization Term),它用于惩罚模型的复杂度。
在下一篇文章中,我们将完成损失函数 $L(W)$ 的完整拼图,深入理解正则化项 $\lambda R(W)$ 的作用、常见形式(如L1、L2正则化)以及它如何帮助模型获得更好的泛化能力。