
元旦期间,DeepSeek 发布的 mHC 论文在 AI 社区引发了广泛关注。
简而言之,DeepSeek 提出的流形约束超连接(mHC)对传统 Transformer 架构进行了革新。它将单一残差流扩展为多流并行架构,并引入 Sinkhorn-Knopp 算法将连接矩阵约束在双随机矩阵流形上,从而解决了超连接(HC)在大规模训练中因破坏恒等映射而导致的数值不稳定与信号爆炸问题。
时至今日,这篇充满数学推导的论文依然是技术讨论的热点,对其进行解读和分享俨然成为了一种技术时尚。


但行动比解读更为硬核。近日,FlowMode 的工程师 Taylor Kolasinski 宣布,他成功复现了 DeepSeek 的 mHC,并且在测试中观察到了比原始论文报告更惊人的现象。

这一成果在社区中引起了“不明觉厉”的反响。
目前,Kolasinski 正通过系列博客文章详细介绍其复现过程与发现,现已发布两部分内容。

博客一:当残差连接发生爆炸
我们熟知的每一个 Transformer 模型,其核心都离不开自 2016 年沿用至今的同一种残差连接设计。
无论是 GPT、Claude、Llama 还是 Gemini,在底层进行的操作本质相同:x + F(x)。信息沿着单一通道流过网络,每一层都向其添加内容。
而 DeepSeek 提出了一个颠覆性的问题:如果让这个信息流变得更“宽”会怎样?
实验设置
标准残差连接是现代 Transformer 的基石,其思想简洁明了:
x_{l+1}=x_{l}+F(x_{l})
输入信号近乎原封不动地向前流动,并与该层的输出相加。这形成了一条单一、干净的信息路径,确保了梯度可以顺畅地反向传播。正是这种简单性和稳定性,使得 Transformer 能够堆叠至数百层深度。
超连接(Hyper-Connections, HC)则采取了截然不同的思路。它不再局限于单一流,而是扩展到 n 条并行流,并引入了可学习的混合矩阵:
x_{l+1}=H^{res}_lx_l+H^{post,T}_lF(H^{pre}_lx_l,W_l)
下图直观对比了标准残差连接与超连接的结构差异:
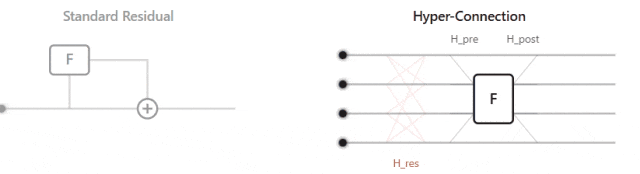
三个关键矩阵掌控着信息流向:
- H_res:控制信息在残差路径中如何混合。
- H_pre:决定信息在进入层之前如何组合。
- H_post:负责将层的输出分配回各条流中。
超连接理论上具有更强的表达能力,且增加的参数带来的计算开销微乎其微。然而,问题在于这些混合矩阵是不受约束的。它们不仅能路由信号,还可能放大信号。
不稳定性显现
在激进的学习率设置下,复现实验中的超连接出现了高达 7 倍的信号放大,并最终导致训练崩溃。这里用 Amax(矩阵行和列绝对值的最大值)来衡量信号放大程度。
在 1000 万参数的小规模实验中,这种不稳定性尚可容忍。但 DeepSeek 在其 270 亿参数的模型上观察到了更严峻的情况:
“Amax 增益幅度产生了极值,峰值达到 3000。”
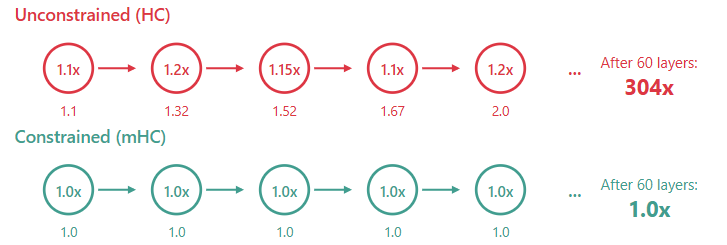
这意味着三千倍的信号放大!在超大模型规模下,不受约束的 HC 不仅会漂移,更会爆炸。小规模实验中的 9.2 倍放大,正是这种指数级故障的早期预警。
因此,不受约束的混合矩阵在规模化时必然崩溃,微小的放大效应会通过层层累积产生指数级增长。
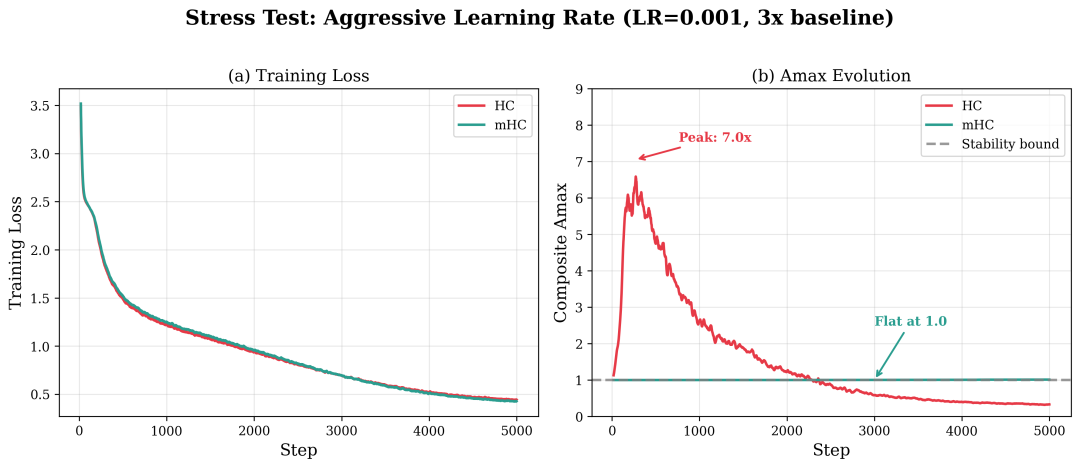
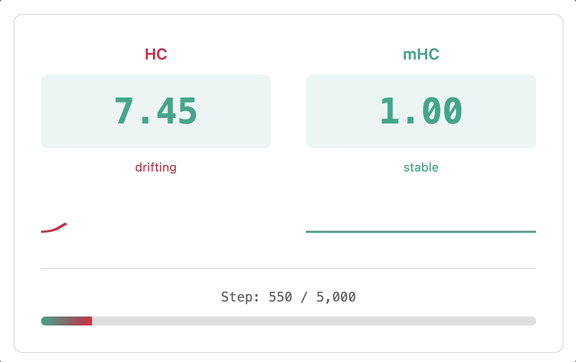
压力测试:在激进学习率下,HC 的信号放大在崩溃前达到 7 倍,而 mHC 始终稳定在 1.0。
解决方案:流形约束
DeepSeek 的解决方案清晰而巧妙:将混合矩阵约束为双随机矩阵。
一个双随机矩阵满足:
- 所有元素均为非负数。
- 每一行元素之和为 1。
- 每一列元素之和为 1。
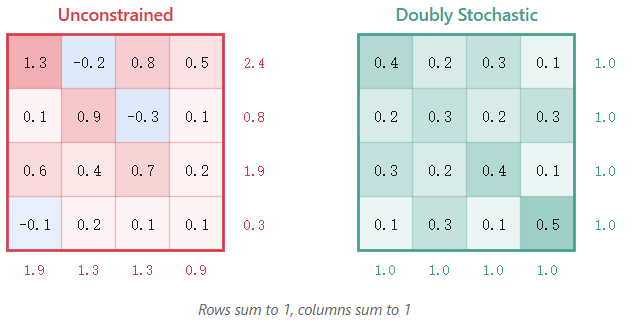
这意味着混合操作只能对流进行加权平均。它可以路由、重排、融合信息,但无法放大信息。
如何实现这一约束?DeepSeek 使用了 Sinkhorn-Knopp 算法。
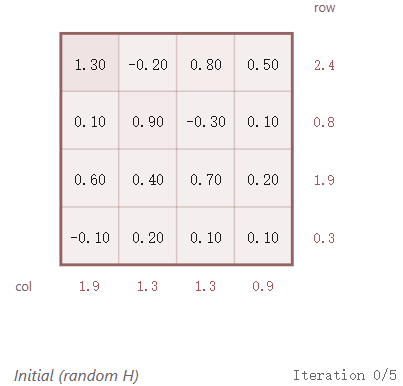
该算法步骤简单:
- 从任意矩阵(即模型学习到的原始权重 H)开始。
- 对矩阵元素取指数,确保所有值为正:
P = exp(H)。
- 归一化行,使每行之和为 1。
- 归一化列,使每列之和为 1。
- 重复步骤 3 和 4,直至收敛(通常约20次迭代)。
这个过程是完全可微分的,梯度可以反向传播穿过所有迭代步骤。网络学习的是原始权重 H,而 Sinkhorn 变换确保了实际使用的混合矩阵始终是双随机的。
P^{(t+1)}=ColNorm(RowNorm(P^{(t)}))
技术细节上,只有递归混合矩阵 H_res 需要完整的 Sinkhorn 双随机处理,因为它是导致误差逐层复合的关键。而输入/输出混合器 (H_pre, H_post) 仅通过有界函数(如 sigmoid)进行约束,从而将计算成本集中在最需要的地方。
复现结果分析
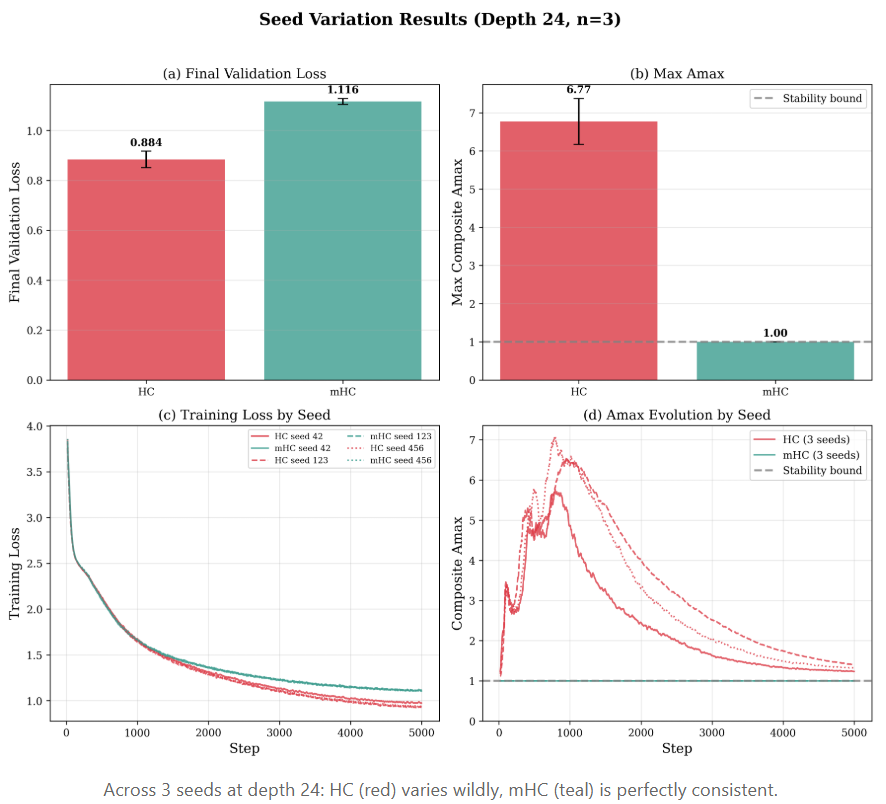
不同随机种子下的结果对比(深度24,3个种子)

在小规模(1000万参数)实验中,无约束的 HC 在原始性能上略胜一筹:验证损失为 0.88,而 mHC 为 1.12。此时,mHC 的稳定性约束像是一种“表达能力税”。
然而,观察方差则揭示出另一番景象。HC 的损失在不同随机种子间的波动是 mHC 的 3 倍(±0.033 vs ±0.012)。至于 Amax 值,HC 在 6.1 到 7.6 之间剧烈摆动,而 mHC 则稳定在 1.00,零方差。
在 1000 万参数下,这种不稳定性尚可存活,HC 仍能完成训练。但当规模扩大到 270 亿参数时,6-7 倍的放大就会演变成 3000 倍的爆炸。在这种量级上,任何不稳定性都是不可接受的赌博。
深度扩展实验
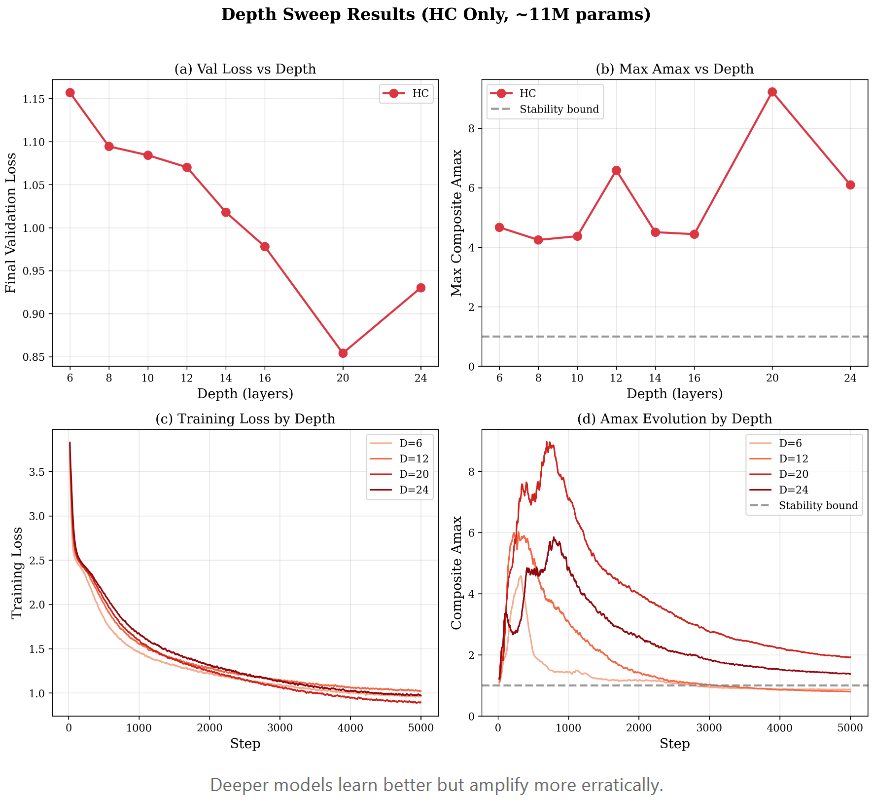
研究还扫描了从 6 层到 24 层的深度(保持总参数量约 1100 万不变):
- 损失随深度增加而改善,在深度 20 处达到最佳(验证损失 0.85)。
- 深度 24 时性能略有下降(损失 0.93),这是由于为了维持参数量而缩窄了模型宽度导致的瓶颈。
- Amax 表现出不可预测的混沌特性:深度 20 时飙升至 9.2 倍,深度 12 时为 6.6 倍,深度 8 时保持在 4.3 倍,没有清晰规律。
实验细节:
- 数据集:TinyShakespeare(约 100 万字符,字符级别)。
- 模型:GPT-2 架构,约 1000 万参数。
- 训练:5000 步,AdamW 优化器,余弦学习率衰减。
- 硬件:Apple M 系列芯片(使用 MPS 后端)。
- 深度扫描:8种配置(6-24层),调整宽度以维持参数量。
- 种子变异:3个不同随机种子(42, 123, 456)。
核心洞见:守恒定律
残差连接不仅仅是一个便于梯度流动的技巧,它实质上是一种守恒定律。
在物理学中,守恒定律约束了系统的可能性,但使得预测变得可能。类似地,残差连接中的恒等映射约束了网络,但保证了稳定性——信号幅度得以保存。
HC 打破了这一定律,而 mHC 则通过将其约束在双随机矩阵流形上,重新“立法”,恢复了信号的守恒。这不是一种回归,而是找到了一条更丰富、同时依然守恒的信号通路。
关键收获
- 架构性错误难以察觉:最初的实现看似正确,公式、代码均无误。但一个关键的架构理解偏差——未能维持层间真正的并行流——使得“超连接”名不副实。这提醒我们,在实现新颖架构时,必须反复审视数据流的实际形状。
- 约束即保障:双随机投影不是限制,而是强制性的稳定保证。它并非让模型“学会”稳定,而是直接使不稳定的行为变得不可能。在稳定性至关重要的场景下,这种“束缚”是可贵的。
- 稳健性优于极端表达力:标准残差连接自 2016 年沿用至今,并非因为最优,而是因为极其稳定。HC 表达力强但脆弱,mHC 则找到了一个平衡点:比标准残差更具表达潜力,同时带有坚实的稳定性保障。
博客二:17亿参数下的不稳定炸弹
在系列的第一部分,我们在 1000 万参数规模下目睹了超连接将信号放大 9.2 倍。而 DeepSeek 论文报告在 270 亿参数下放大倍数达到了 3000 倍。那么,当我们将实验规模大幅提升,会发生什么?
为此,我们租用了一个 8x H100 的计算节点进行了一次 大规模模型训练实验。以下是令人震惊的发现。
规模跃迁:从 9.2 倍到 10924 倍
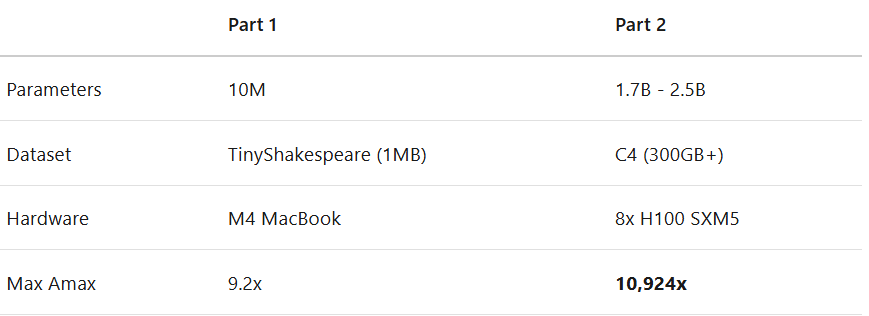
10924 倍信号放大! 这个数字远远超出了 DeepSeek 论文中报告的 3000 倍。
实验设计
本次实验涵盖了三种架构,共 18 次运行:
- Residual:标准残差结构
x + F(x),作为基线。
- HC:使用无约束混合矩阵的超连接。
- mHC:使用 Sinkhorn 投影的流形约束超连接。
每种架构在两种网络深度(32层和48层)下,分别使用三个随机种子(42, 123, 456)进行训练,以确保结果的可靠性。所有模型在 C4 数据集上训练 5000 步,采用 bf16 混合精度。其中,32 层模型参数量为 17.3 亿(1.73B),48 层模型为 25.4 亿(2.54B)。
主要发现
首先,在损失曲线上,所有方法最终都收敛到相似的区间(约 5.4–6.0)。学习曲线几乎重合,表明引入 Sinkhorn 投影的 mHC 算法 几乎没有带来额外的性能代价。
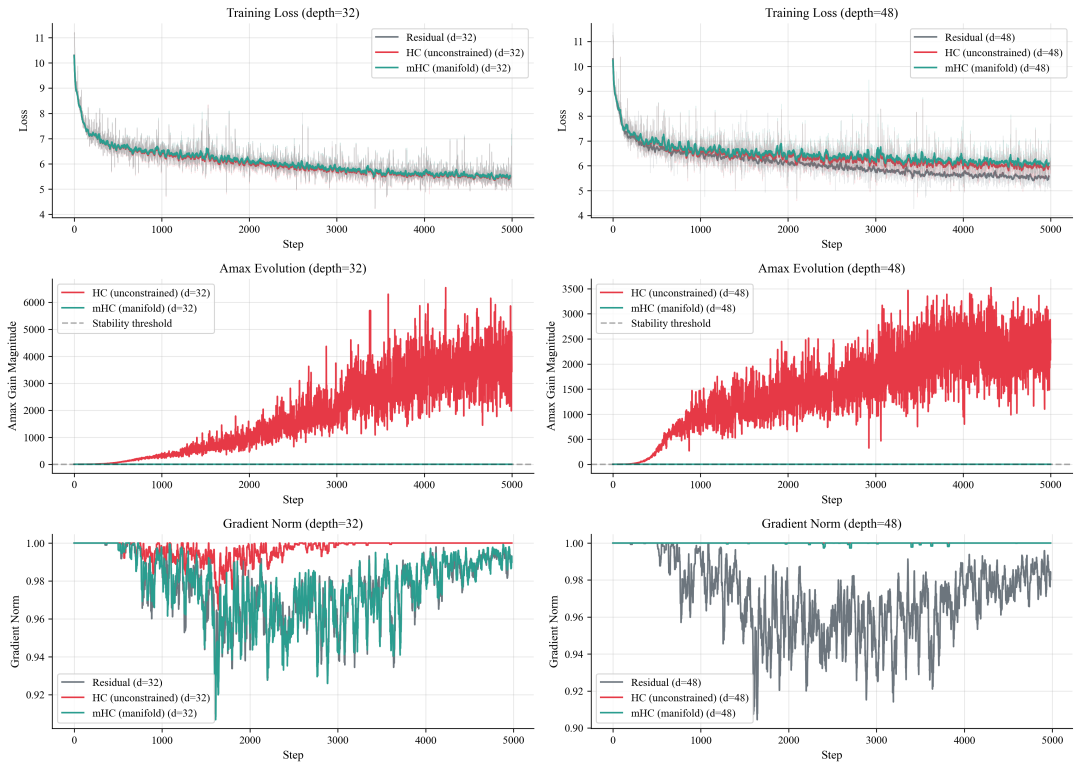
然而,在稳定性指标 Amax 上,差异堪称天壤之别。Amax 衡量混合矩阵对信号的放大程度,1.0 表示中性(不放大),数值越高,放大越强。
实验显示,在深度 32 的模型中,HC 的 Amax 值飙升至 6500 倍以上并剧烈波动,而 mHC 则牢牢锁定在 1.0。在深度 48 的模型中,这一模式重现:HC 暴涨至约 3500 倍,mHC 依然稳定。
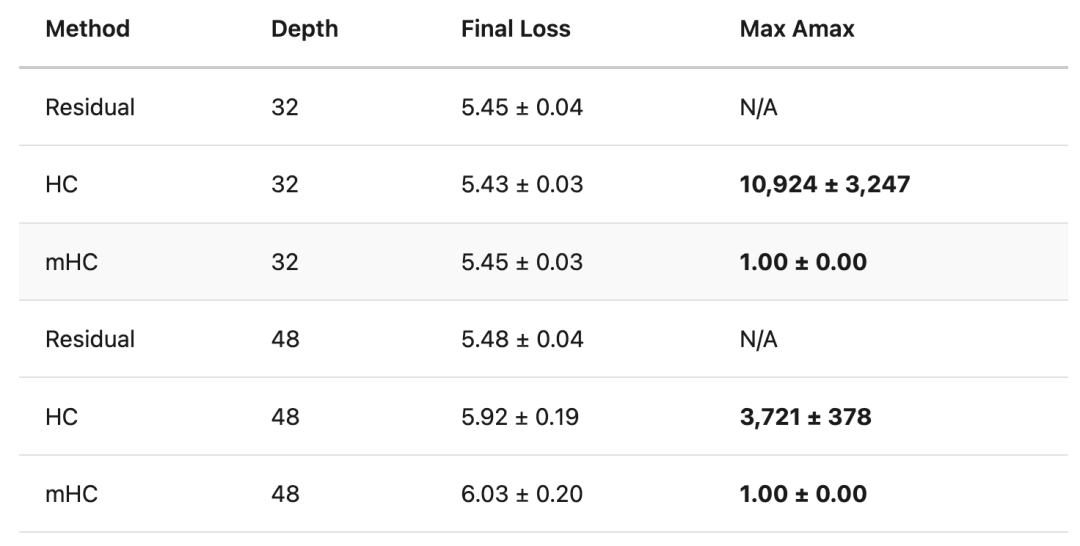
缩放定律:不稳定性随规模激增
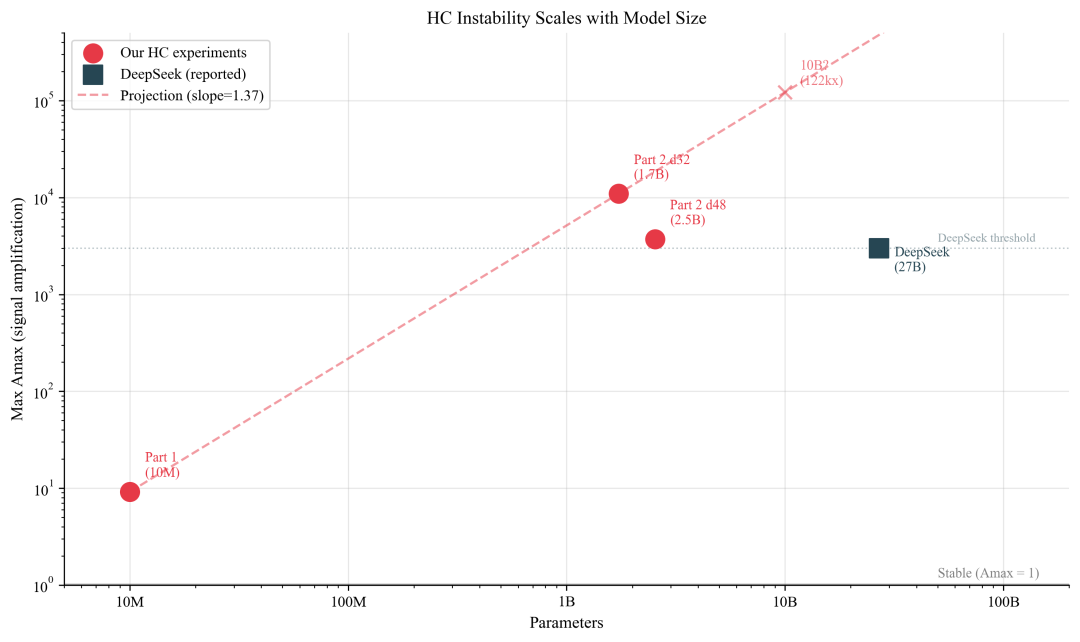
将 Amax 与模型参数规模绘制在双对数坐标轴上,可以清晰看到一条急剧上升的趋势线:
- 1000 万参数时,Amax ~ 9.2 倍。
- 17 亿参数时,Amax 跃升至 10924 倍。
- 作为参照,DeepSeek 报告的 270 亿参数模型 Amax ~ 3000 倍。
根据趋势线外推,当模型规模达到 100 亿参数时,Amax 可能升至约 50,000 倍;在 1000 亿参数量级,甚至可能接近 400,000 倍。实验结果显示,不稳定性并未出现自我修正的迹象,反而随着模型规模扩大持续加剧。
高度可复现的模式
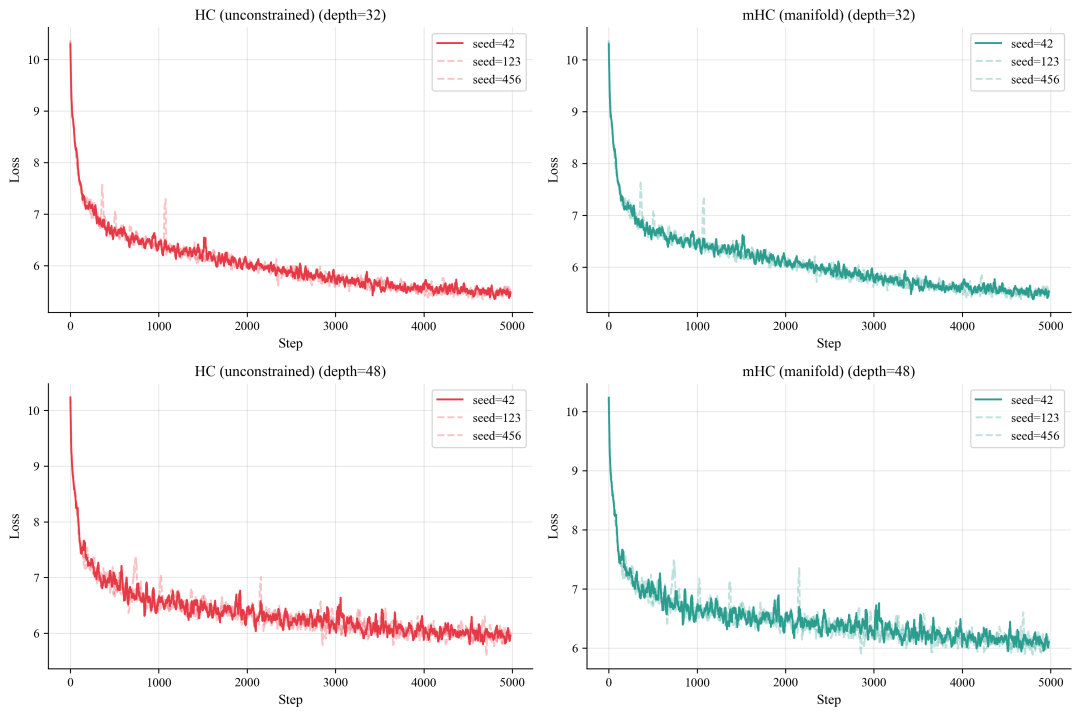
在三个不同的随机种子下,实验呈现出完全一致的模式:所有 HC 运行都发生了“爆炸”,而所有 mHC 运行都保持平稳。不同种子下的损失曲线几乎重叠,学习速度一致。唯一的区别在于模型内部:HC 在不断积累不稳定性,而 mHC 则始终保持结构完整。
逐层分析:祸起“萧墙”
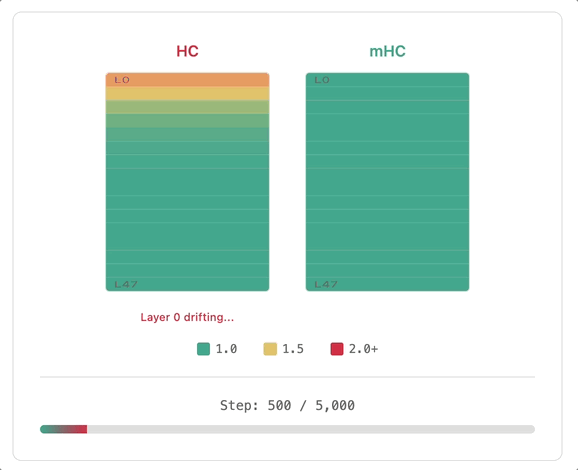
一个令人惊讶的发现是:不稳定性始于网络的最输入端(第 0 层),而非深层。
在 HC 中,第 0 层的混合矩阵最早变红,其 Amax 值在训练初期就突破 2.0,而更深层反而相对稳定。这是因为第 0 层直接处理原始的嵌入向量,前面没有层归一化(LayerNorm)为其“把关”。它必须直接应对嵌入表输出的任何数值尺度,若尺度不匹配,它便会学习“补偿”,而在 HC 中,补偿往往意味着放大。
反观 mHC,在所有层级和所有训练步数中均呈现均匀的绿色,Sinkhorn 投影在限制放大的同时,也彻底防止了任何层的漂移。
信号流的可视化
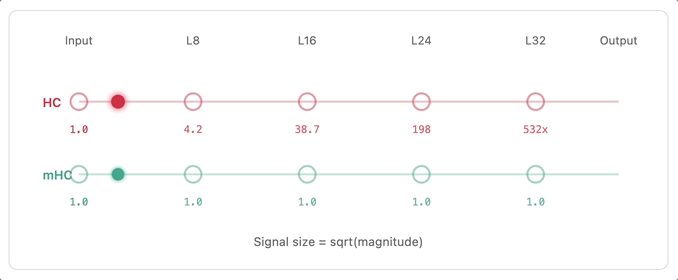
在训练的第 3000 步,一个输入 HC 网络的信号在输出时被放大了 532 倍。而同样的信号经过 mHC 网络后,放大倍数仅为 1.000003 倍,几乎保持不变。层归一化和非线性激活函数似乎“收拾”了 HC 产生的大部分混乱,但这意味着它们消耗了本可用于学习的模型容量,仅仅是为了抵消上游制造的问题。
这再次印证了守恒定律的重要性:残差连接应当保持信号幅度。HC 打破了规则,而 mHC 坚守了底线。
压力测试:推向极限
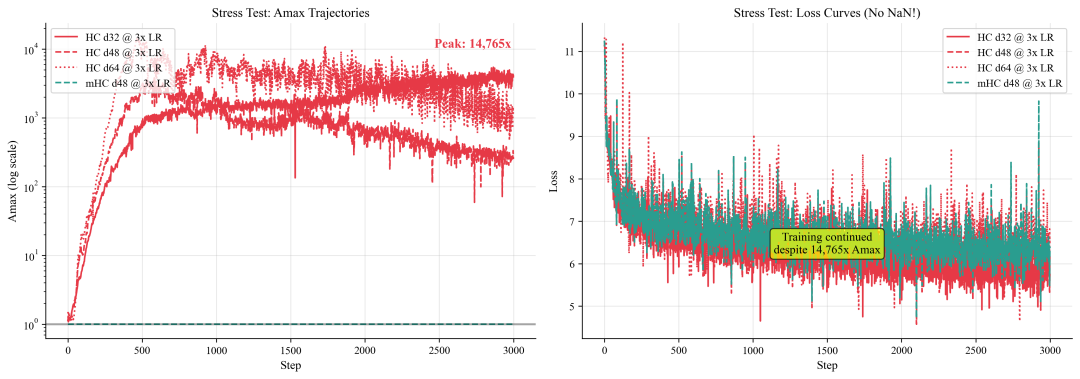
在正常训练使用 1e-4 学习率的基础上,我们进行了 3 倍学习率(3e-4)的压力测试。

深度 64 的 HC 模型,其 Amax 达到了惊人的 14765 倍,并在 2000 倍到 10000 倍之间剧烈振荡,混合矩阵完全失控。而 mHC 在所有配置和学习率下,依然表现得平坦、稳定,数值恒为 1.0。
意料之外:尚未引爆的炸弹
一个出乎意料的结果是:尽管 Amax 高达上万倍,但所有 HC 实验在 5000 步内并未崩溃。损失没有发散,训练也未产生 NaN,模型仍在继续学习。
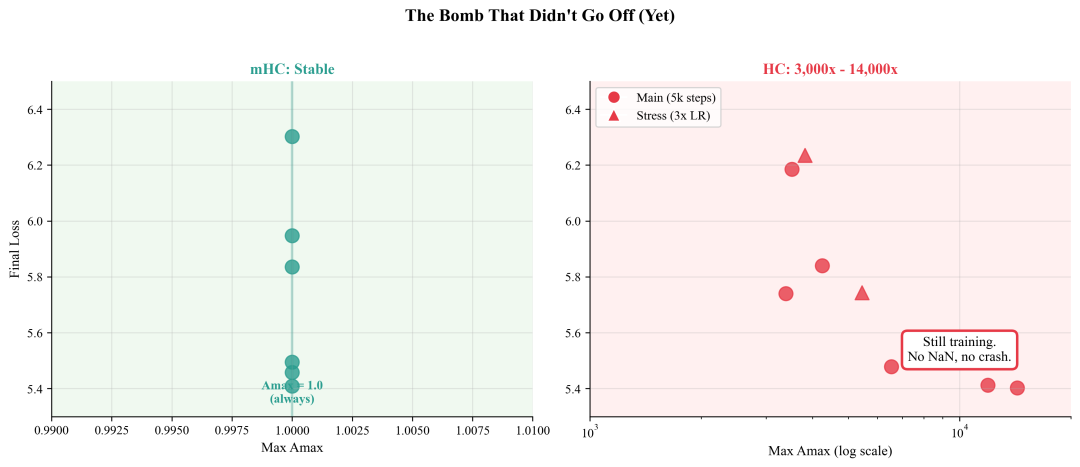
这形成了一种“定时炸弹”情景。不稳定性真实存在且非常严重,但尚未导致即时灾难。可能的原因包括:
- 梯度裁剪:将梯度范数裁剪在 1.0,很可能防止了最严重的爆炸。
- 训练步数不足:更长的训练可能最终引发崩溃。
- 模型规模仍不够大:在千亿参数规模下,动力学特性可能发生质变。
最稳妥的结论是:HC 正在积累不稳定性风险,该风险在某些条件下可能被引爆;而 mHC 则完全消除了这类风险。
实践要点总结
如果你正在实现或使用超连接:
- 务必使用 Sinkhorn 投影:仅需约 10 行代码,即可消除一种在大规模训练中极为危险的故障模式。
- 监控训练中的 Amax:如果发现其持续上升并超过 10 倍,则表明不稳定性正在积聚。
- 密切关注第 0 层:输入混合矩阵是稳定性的“金丝雀”。基础模型第 0 层的不稳定,可能在微调时因词表变化或嵌入漂移而引发问题。
- 约束没有性能代价:实验表明,mHC 的最终损失与 HC 相当,稳定性是“免费”的。
实验数据已公开,训练代码仓库即将发布。
- 主要实验数据: wandb.ai/taylorkolasinski/mhc-part2
- 压力测试数据: wandb.ai/taylorkolasinski/mhc-part2-stress
实验运行于 Lambda Labs 的 8x H100 SXM5 节点,耗时约 17 小时。
未解之谜与未来方向
两个关键问题依然悬而未决:
- HC 最终会失败吗? 我们看到了 10924 倍的放大,但训练并未发散。这是否只是一种潜在风险?还是说更长的训练必然导致失败?
- 确切的缩放定律是什么? 从 1000 万参数的 9.2 倍,到 17 亿参数的 10924 倍,若扩展到 100 亿参数,按照趋势可能达到 50000 倍放大。这需要更大的计算预算进行探索。
这项复现研究不仅验证了 DeepSeek 论文的核心观点,更以惊人的数据揭示了无约束超连接在规模化时的巨大风险,并证明了流形约束的有效性与必要性。对于致力于 探索人工智能前沿架构 的研究者和工程师而言,这些发现提供了宝贵的实践见解。