随着语言模型能力的不断增强,用户不再满足于其仅仅提供准确的答案,更希望模型的行为能够在多样化场景中与复杂的人类偏好对齐。为了实现这一目标,强化学习训练流程越来越多地引入多个奖励信号,每个奖励负责捕捉一种特定的行为偏好。然而,直接将先前广泛使用的 GRPO 方法应用于多奖励设置时,研究者发现了一个严重问题:对不同的奖励组合进行简单归一化,可能导致它们坍塌为相同的优势值,从而削弱了训练信号的分辨能力,最终导致模型收敛到次优解,甚至在训练早期就遭遇失败。
为此,英伟达的研究团队提出了一种全新的策略优化方法——GDPO (Group reward-Decoupled Normalization Policy Optimization)。GDPO 的核心思想是对每个奖励信号分别进行解耦的归一化处理,从而更真实地保留不同奖励之间的相对差异。这不仅实现了更精准的多目标优化,也显著提升了训练的稳定性。研究团队在工具调用、数学推理和代码推理这三类典型任务上,对 GDPO 与 GRPO 进行了系统性对比。实验结果表明,在所有测试设置下,GDPO 的表现均稳定超越 GRPO,充分验证了其在多奖励强化学习场景中的有效性和出色的泛化能力。

方法
(1)GDPO
GDPO 的设计思路与 GRPO 截然不同。GRPO 首先将全部 n 个奖励相加,然后再对这个总和进行组内归一化,得到总优势值 A_sum。而 GDPO 则针对第 i 个问题的第 j 次 rollout,分别为每一个奖励单独计算归一化后的优势值:
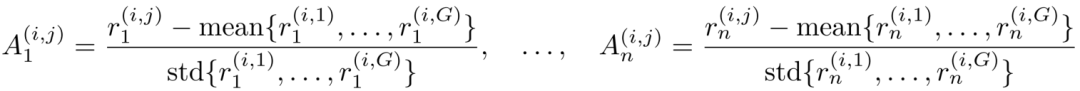
随后,将各个奖励维度上已经归一化的优势值求和,得到用于策略更新的总体优势值:
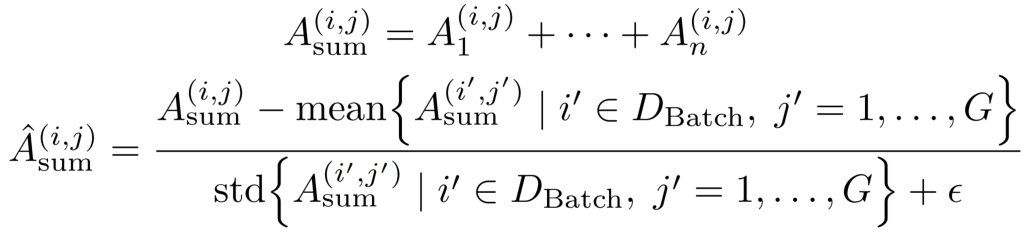
最后,还需要对这个多奖励优势值的求和结果施加一次批级别的优势归一化,以确保最终优势值的数值尺度保持稳定,不会因为引入更多奖励项而无限制地增大。
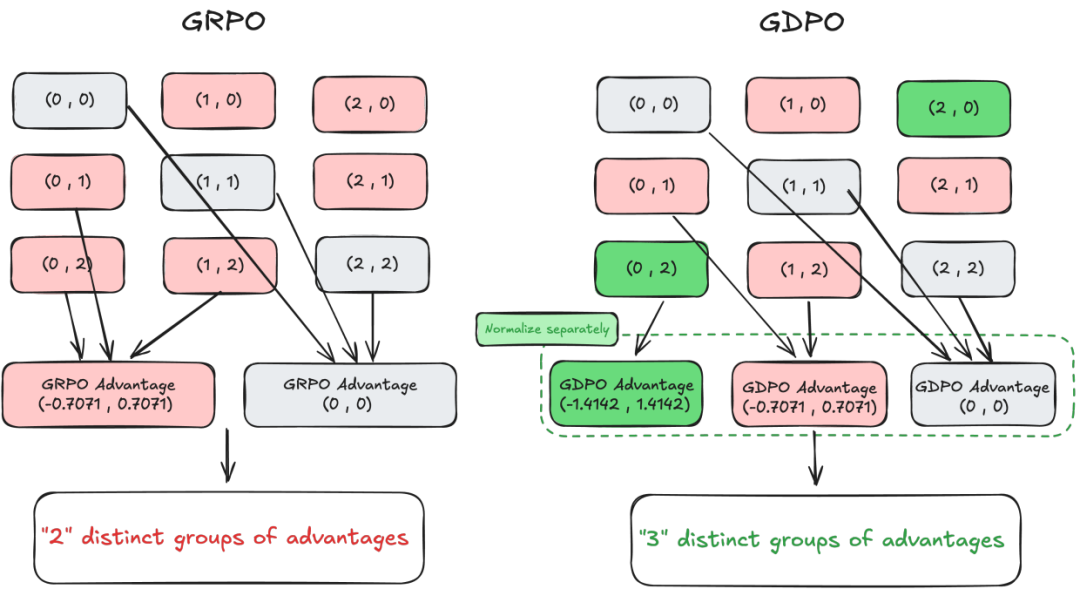
图2 在包含两个二元奖励、两个 rollout 的示例中,GRPO 与 GDPO 的优势值计算对比
通过为每个奖励单独进行归一化,GDPO 有效地缓解了 GRPO 在优势值估计中造成的信息丢失问题。如图 2 所示,在 GRPO 中,不同的奖励组合(例如 (0,1) 和 (0,2))可能会被映射为相同的优势值,从而掩盖了它们之间存在的细微差异。而 GDPO 则为它们分配了不同的优势值(例如 (−0.7071, 0.7071) 与 (−1.4142, 1.4142)),更合理地反映出 (0,2) 组合应当提供更强的学习信号这一事实。
类似地,当扩展到三个 rollout 时,GRPO 会将所有总和相同的组合(例如来自不同奖励分布的 (1,1,0) 和 (0,0,1))统一归为优势值 (0,0,0)。而 GDPO 能够保留各个维度的差异,生成非零且有区分度的优势值,从而更好地捕捉多奖励结构中所蕴含的语义信息。
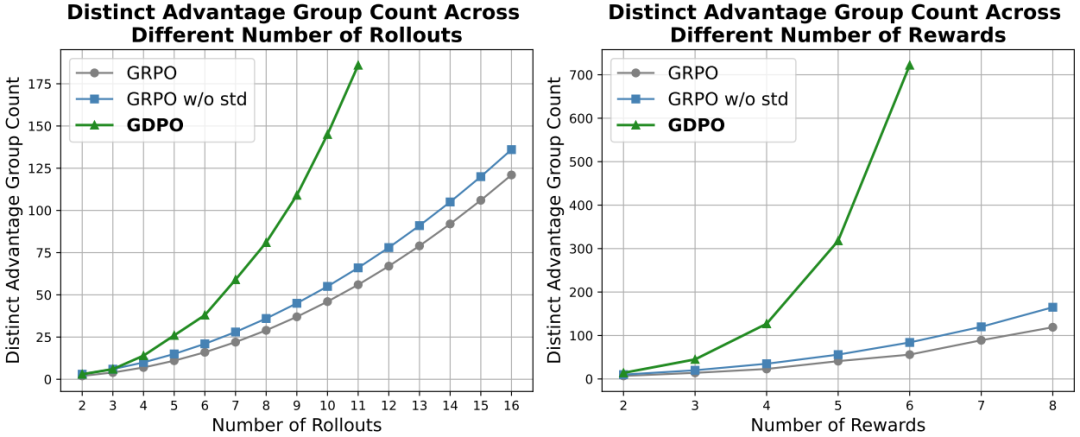
图3 不同方法生成的互异优势值组数量对比。随着 rollout 数量(左)或奖励维度数(右)增加,GDPO 始终显著优于 GRPO 及其变体(GRPO w/o std),保留更多优势值区分度
为了量化 GDPO 的有效性,研究团队进一步比较了 GDPO、GRPO 以及不带标准差归一化的 GRPO 变体(GRPO w/o std)在不同实验设置下所产生的“互异优势值组”数量,结果如图 3 所示。
在双奖励场景中,随着 rollout 数量的增加,GDPO 始终能生成显著更多的互异优势值组,并且这一优势差距随着 rollout 数量的增长而进一步扩大。另一方面,在固定 rollout 数量为 4、逐步增加奖励数量的设置下,也呈现出类似的趋势:随着优化目标(奖励维度)的增多,GDPO 表现出的优势值粒度越来越精细。这表明,GDPO 所采用的解耦归一化方法,能够在各类强化学习设置中有效提升优势估计的精确性。
(2)有效整合优先级变化
研究团队系统地梳理了实现目标优先级的两种常见方法:一是调整不同目标对应奖励的权重,二是直接修改奖励函数本身。同时,他们分析了当各个目标的基础奖励在优化难度上存在显著差异时,这两种方法的行为区别。
当底层目标的难度差异较大时,单纯调整奖励权重可能无法实现预期效果。如果某一目标显著更容易优化,模型往往会优先最大化其奖励,而忽略人为分配的权重差异。因此,要想让模型更关注更具挑战性的目标,权重差异必须足够大以抵消难度差距。即便如此,模型仍可能倾向于优化简单的目标,而非用户真正重视的那个。
为了应对多奖励强化学习中常见的“奖励作弊”问题,近期有工作提出将较易优化的奖励 r_k 条件化于更关键但更难优化的奖励 r_l。具体而言,只有当 r_l 达到预设的阈值 t 时,模型才能获得 r_k 的奖励;否则 r_k 被置为零。
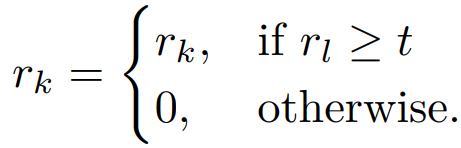
这种设计强制模型必须优先确保高优先级目标达标,之后才有可能从次要目标中获益。它有效地避免了模型“走捷径”,显著缓解了因任务难度差异导致的优化偏差,从而使模型的学习行为能更好地与人类的真实偏好对齐。
评估
(1)工具调用能力
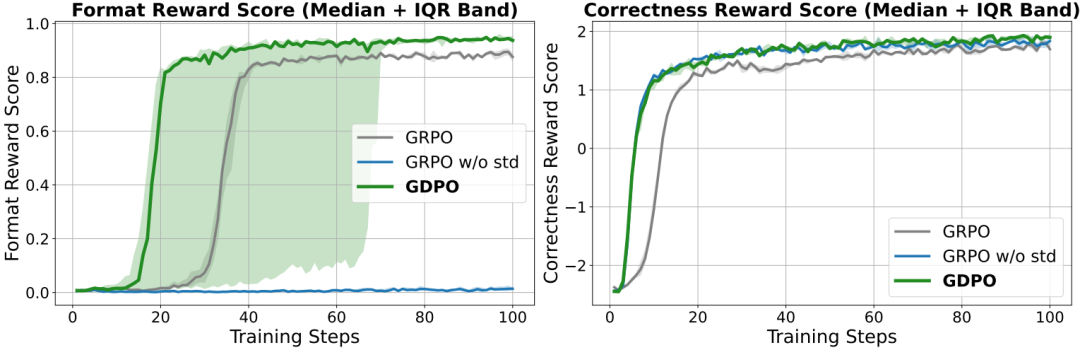
图4 在 Qwen2.5-1.5B 模型上进行五次独立运行工具调用任务的中位数及四分位距奖励曲线
如图 4 所示的训练曲线表明,在所有独立运行中,GDPO 在格式奖励和正确性奖励两个指标上,最终都收敛到了比 GRPO 更高的数值。尽管收敛步数存在波动,但 GDPO 在格式正确性上最终表现更优。在正确性奖励方面,GDPO 在训练早期提升更快,并在后期达到了比 GRPO 基线更高的分数,这证明 GDPO 能提供更准确的优势估计,从而实现更优的策略优化。

表1 利用GDPO 与 GRPO 训练的 Qwen2.5-Instruct-1.5B/3B 模型在工具调用准确率与格式正确性对比
在 BFCL-v3 评测集上的结果(见表 1)进一步证实了这一点。GDPO 在平均工具调用准确率和格式正确性方面,始终优于使用 GRPO 训练的对应模型。 在 Qwen2.5-Instruct-1.5B 的训练中,GDPO 在 Live 与 non-Live 任务上分别提升了近 5% 和 3%,整体平均准确率提升约 2.7%,且格式正确率提高了超过 4%。在 3B 模型上也观察到了类似的提升趋势。

图5 GRPO 与 GDPO 在 DeepSeek-R1-1.5B 模型上的训练行为对比
从图 5 所示的 DeepSeek-R1-1.5B 模型的训练曲线中,我们可以观察到一些更深层次的现象。首先,无论采用哪种优化方法,模型都倾向于优先最大化更容易优化的奖励。在此任务中,长度奖励更容易优化,因此 GRPO 和 GDPO 均在训练开始约 100 步内就达到了满分。
同时可以看到,长度奖励的快速上升与正确性奖励的早期下降是同步发生的,这表明这两个奖励目标之间存在竞争关系。在训练初期,模型优先满足长度约束,往往以牺牲更具挑战性的正确性目标为代价。
此外,从正确性奖励的轨迹来看,GDPO 能比 GRPO 更有效地恢复并提升正确性得分,在相同训练步数下取得更高的性能。 值得注意的是,GRPO 的训练在大约 400 步后开始出现不稳定迹象,正确性得分逐渐下降;而 GDPO 则持续提升正确性得分,展现了更强的优化能力和训练稳定性。
尽管 GRPO 几乎达到了满分的长度奖励,但其最大响应长度在训练约 400 步后开始急剧上升;而 GDPO 的最大响应长度则持续下降,这表明 GDPO 始终能更好地遵循长度约束。
(2)数学推理能力
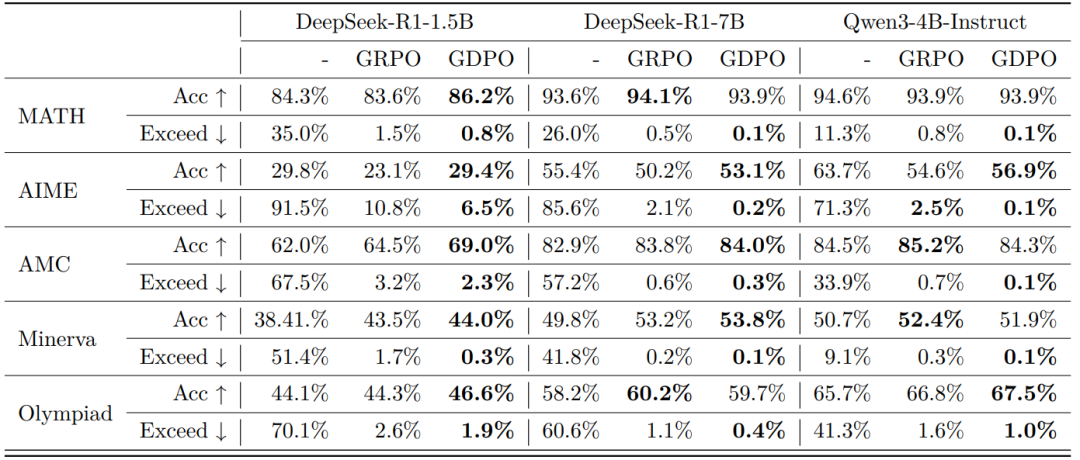
表2 GDPO 与 GRPO 训练的 DeepSeek-R1-1.5B/7B 模型在数学推理基准上的准确率及超出长度约束的比例对比
表 2 的基准结果表明,GDPO 训练的模型不仅在遵循约束上显著优于原始模型(如在 AIME 上响应长度超限率最高降低 85%),还在多数任务上取得了更高的准确率。
在 DeepSeek-R1-1.5B 上,GDPO 在 MATH、AIME 和 Olympiad 上的准确率分别提升了 2.6%、6.7% 和 2.3%,同时全面降低了响应长度超限率。类似的趋势也出现在 DeepSeek-R1-7B 和 Qwen3-4B-Instruct 上。尤其在更具挑战性的 AIME 任务中,GDPO 将准确率提升了近 3%,并将响应长度超限率大幅降至 0.2% 和 0.1%,远优于 GRPO 的 2.1% 和 2.5%。这些结果共同表明,GDPO 能在提升数学推理准确率的同时,更有效地促使模型遵守长度约束。
为了探究将较易优化的长度奖励以更具挑战性的正确性奖励为条件,是否有助于缓解目标间的难度差异并提升优先级对齐效果,研究团队将原始的长度奖励 R_length 替换为条件化的长度奖励 R_length_cond。
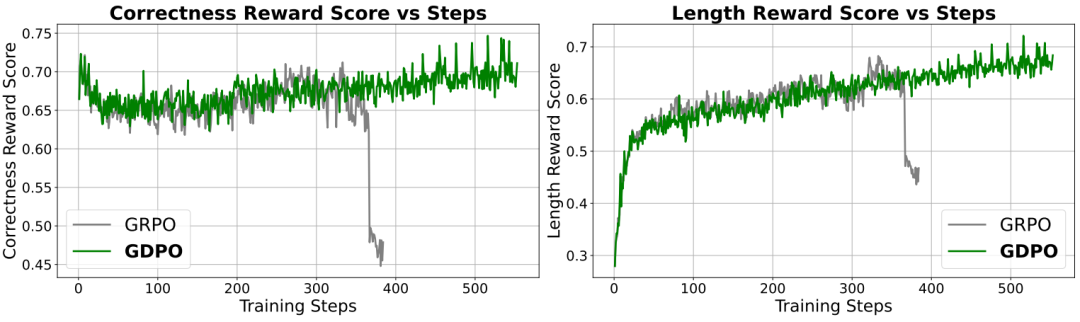
图6 在 DeepSeek-R1-7B 上使用条件化长度奖励时,GRPO 与 GDPO 的训练曲线
采用修改后的奖励函数后,能有效防止模型在训练初期过度追求长度奖励。这种设计也有助于避免模型在满足长度约束时导致正确性奖励大幅下降。如图 6 所示,平均正确性奖励仅在训练早期轻微降低,随后便逐步恢复。
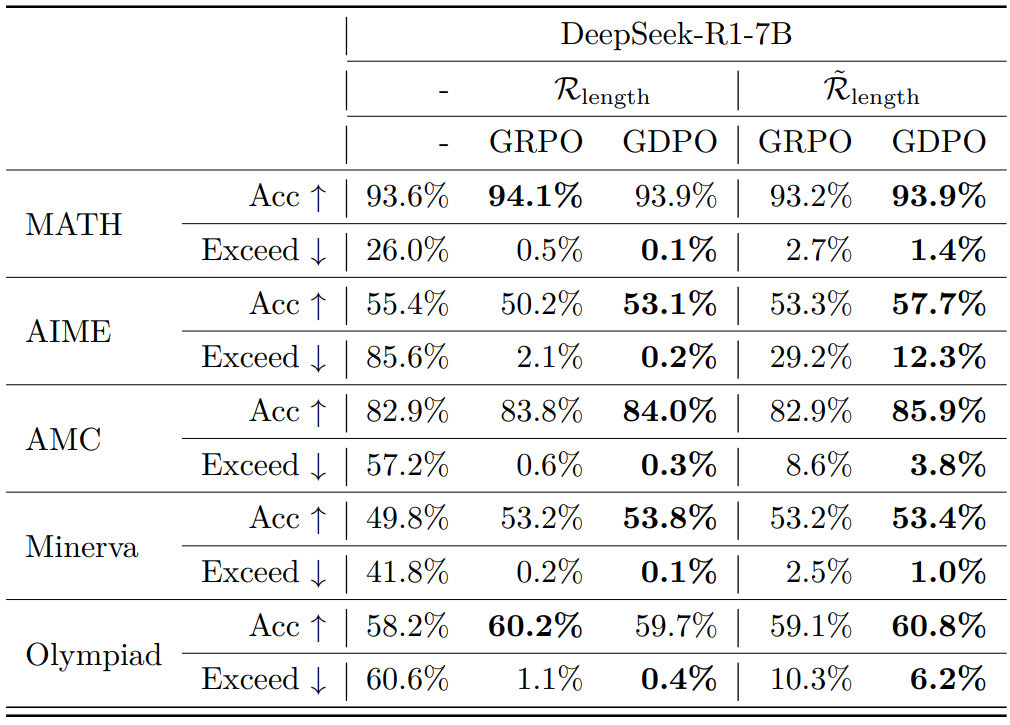
表3 在数学推理基准上,采用与未采用条件化长度奖励时,GRPO 与 GDPO 训练的 DeepSeek-R1-7B 模型对比
如表 3 所示,使用条件化长度奖励会导致 GRPO 和 GDPO 的平均长度超限率有所上升,表明该方法确实放松了长度约束。然而,GRPO 未能将这种约束放松转化为准确率的提升。相比之下,GDPO 能更有效地优化准确性奖励,其训练过程中的准确率提升更为稳定。即使在引入条件化奖励后,GDPO 模型长度违规的增幅也显著小于 GRPO。
(3)代码推理能力
研究团队进一步探究在代码推理任务中同时优化三个奖励时,GDPO 是否仍优于 GRPO。这三个目标分别是:提升代码正确性(通过率)、控制输出长度、以及鼓励生成无缺陷的代码,对应的奖励为 R_Pass, R_length 和 R_Bug。
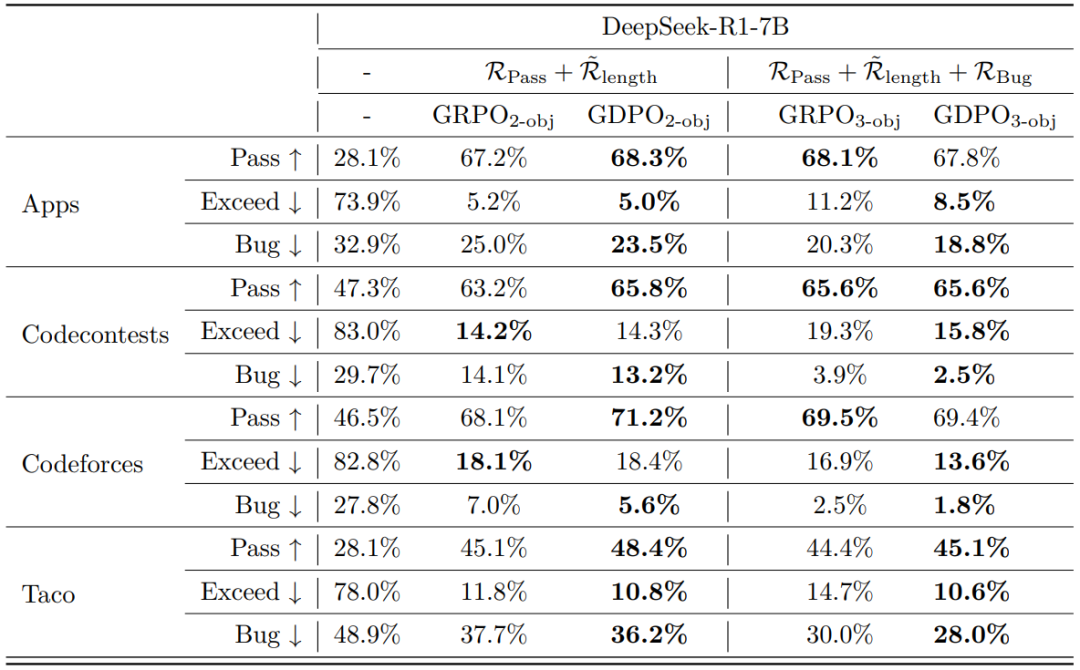
表4 在代码推理基准上,对 GRPO 与 GDPO 训练的 DeepSeek-R1-7B 模型的对比结果
如表 4 所示,在双奖励设置中,GDPO 在所有任务上均提升了通过率,同时其长度超限率与 GRPO 相当。在三奖励设置中,GDPO 同样表现出更优的多目标平衡能力:其通过率与 GRPO 相当,但显著降低了长度超限率和代码缺陷率。总体而言,随着奖励信号数量的增加,GDPO 依然保持其有效性,在双奖励和三奖励配置下均比 GRPO 实现了更优的多目标权衡。
这项研究为解决多奖励强化学习中的优化难题提供了新的思路。对于在人工智能领域深耕的开发者而言,深入理解GDPO这类前沿优化技术,有助于构建更强大、更符合人类复杂偏好的AI系统。更多深度技术讨论与资源分享,欢迎访问云栈社区。