
位置编码(Positional Encoding)是 Transformer 模型里非常关键的一环,但经常被忽视。很多文章画了很好看的位置编码图,却没有把“为什么它能工作”讲清楚。本文尝试补上这块缺口:用更可解释的方式,从直觉到数学性质,再到代码与可视化,系统梳理两类常用位置编码。
前置要求:如果你已经熟悉 Transformer 架构与 self-attention(自注意力)机制,读起来会更顺畅。
问题:序列顺序很重要
在自然语言处理(NLP)和各种序列数据任务里,顺序决定了含义。比如句子:
“The cat sat on the mat.”
你把词语顺序打乱,很可能就变成了无意义的组合,或者语义完全不同。
Transformer 的高效来自并行计算,但并行也带来一个代价:模型本身并不天然理解“顺序”。与 RNN 不同,Transformer 既不靠递归结构,也不靠卷积去隐式编码时序关系,而是更像把每个 token 当成相互独立的点来处理。这对序列任务显然是个大麻烦:没有顺序,注意力怎么知道“谁在谁前面”?
位置编码:解决方案
为了解决上述限制,Transformer 引入了 Positional Encoding。你可以把它理解为“给 embedding 注入位置信息”的方法,让模型在并行计算时依旧能感知序列结构。
位置编码有多种形式,本文聚焦两种常见且重要的方案:
- Absolute Positional Encoding(绝对位置编码,本文主要讲 sinusoidal)
- Rotary Position Embedding(RoPE,旋转位置编码)
并建议你把它们与 Transformer 的注意力计算放在一起理解。
Absolute Positional Encoding(Sinusoidal)
绝对位置编码的方法很多,其中 sinusoidal(正弦/余弦) 因为形式优雅、效果稳定,在论文 Attention Is All You Need(Vaswani et al.)之后被广泛采用,并成为经典基线。
核心思路
Sinusoidal PE 的做法可以概括为:
- 为序列中每个位置生成一个唯一向量(用不同频率的正弦/余弦函数)。
- 该向量的维度与 token embedding 相同(通常记为
$$d_{model}$$
),因此可以直接相加。
- 不同维度对应不同频率:从高频到低频,形成“频率谱”。
- 有一个重要性质:相对位移(offset)可以通过线性方式表示,从而更容易学习相对位置关系。
直觉:从比特到波(From Bits to Waves)
为了建立直觉,我们从一个非常基础的表示开始:二进制。
二进制表示(Binary Representation)
我们看二进制计数:
0: 0 0 0 0 8: 1 0 0 0
1: 0 0 0 1 9: 1 0 0 1
2: 0 0 1 0 10: 1 0 1 0
3: 0 0 1 1 11: 1 0 1 1
4: 0 1 0 0 12: 1 1 0 0
5: 0 1 0 1 13: 1 1 0 1
6: 0 1 1 0 14: 1 1 1 0
7: 0 1 1 1 15: 1 1 1 1
观察每一列(每一位)的变化规律:
- 最右边的 bit(LSB)每次加 1 都翻转(频率 1/2)
- 倒数第二位每两个数翻转一次(频率 1/4)
- 倒数第三位每四个数翻转一次(频率 1/8)
- 依此类推……
也就是说:不同维度携带不同频率的信息。这正是 sinusoidal PE 的直觉来源。只不过二进制是离散的 0/1,而正弦余弦提供了“更平滑、可微、可连续”的表示。
Sinusoidal Positional Encoding 公式与示意
原始 Transformer 给出的做法是:用不同频率的 sin/cos 组合为每个位置生成一个向量(示意图如下)。
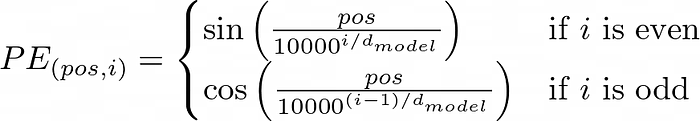
位置编码与 embedding 具有相同维度
$$d_{model}$$
,因此可以相加;其中
$$pos$$
表示位置,
$$i$$
表示维度索引(不同维度对应不同频率的正弦波)。
Python:实现 Sinusoidal PE(代码保持不改动)
下面是生成 sinusoidal positional encoding 的 Python 代码,并画出热力图与部分维度的折线图。
import numpy as np
import matplotlib.pyplot as plt
def sinusoidal_positional_encoding(max_position, d_model):
position = np.arange(max_position)[:, np.newaxis]
# The original formula pos / 10000^(2i/d_model) is equivalent to pos * (1 / 10000^(2i/d_model)).
# I use the below version for numerical stability
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
pe = np.zeros((max_position, d_model))
pe[:, 0::2] = np.sin(position * div_term)
pe[:, 1::2] = np.cos(position * div_term)
return pe
max_position = 100 # Maximum sequence length
d_model = 128 # Embedding dimension
pe = sinusoidal_positional_encoding(max_position, d_model)
plt.figure(figsize=(12, 8))
plt.imshow(pe, cmap='coolwarm', aspect='auto', vmin=-1, vmax=1)
plt.colorbar()
plt.title('Sinusoidal Positional Encoding')
plt.xlabel('Dimension')
plt.ylabel('Position')
plt.tight_layout()
plt.show()
plt.figure(figsize=(12, 6))
dimensions = [0, 21]
for d in dimensions:
plt.plot(pe[:, d], label=f'Dim {d}')
plt.legend()
plt.title('Sinusoidal Positional Encoding for Specific Dimensions')
plt.xlabel('Position')
plt.ylabel('Value')
plt.tight_layout()
plt.show()
运行后你会看到两张图。
可视化 1:Heat map(热力图)
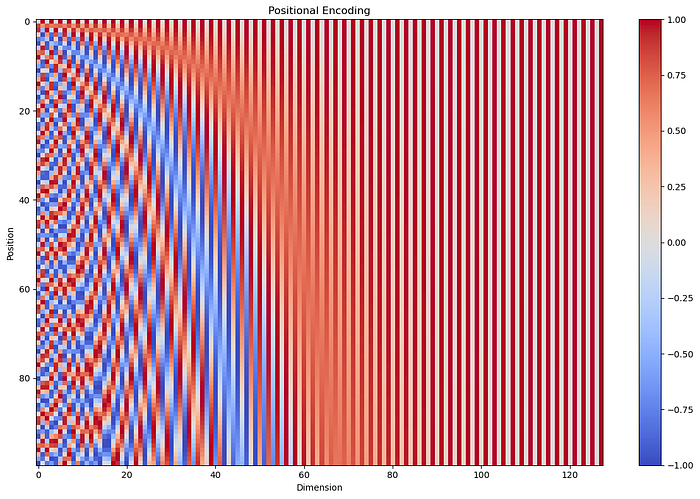
把它类比二进制表格,会更容易读:
- 每一行对应序列中的一个 token(类似二进制表格中的“一个数”)。
- 每一列对应 embedding 的一个维度(类似二进制的“某一位”)。
- 颜色在 -1(蓝)到 1(红)之间连续变化,相当于离散 0/1 的连续版本。
关键观察:
- 第 0 行(position=0)像二进制的 “0000”,是起点。
- 往下走(位置增大),颜色变化呈现出类似“翻转频率”的规律。
- 左侧维度变化更快(高频,类比低位 bit)。
- 右侧维度变化更慢(低频,类比高位 bit)。
可视化 2:Line Plot(某些维度的折线)
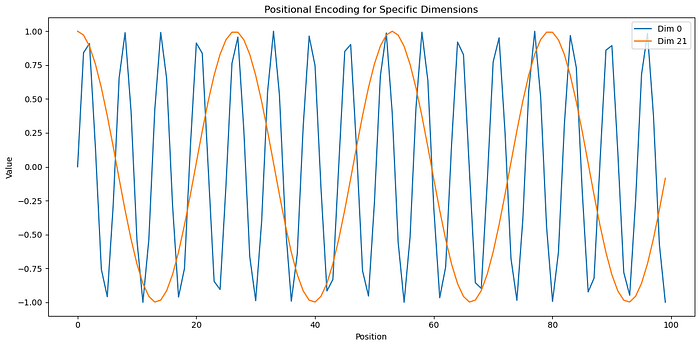
折线图是在追踪单个维度随位置变化的曲线,更像“看某一列 bit 如何翻转”。
关键观察:
- Dimension 0(蓝线)振荡很快,几乎每个位置都变,像二进制最右边的 bit。
- Dimension 21(橙线)变化慢得多,像更高位的 bit。
相对位置(Relative Positioning)为何“可线性表示”?
原始 Transformer 论文中有一句经典说明:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, PE(pos+k) can be represented as a linear function of PE(pos).
直观来说:对于某个固定偏移量(例如往后移动 φ),你希望能用同一个线性变换把当前位置的编码转换成“偏移后”的编码,而不依赖起点位置 t。
对应的数学关系在文中用图展示(以某个频率
$$\omega_k$$
的 sin/cos 对为例):
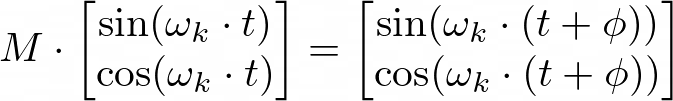
这说明:
$$PE(t+\phi)$$
可以通过一个与 t 无关的矩阵
$$M$$
作用在
$$PE(t)$$
上得到。
证明过程(按原文图示保留):
1)使用三角函数和角公式展开:
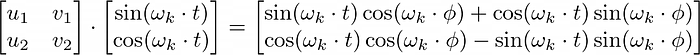
2)得到两条方程(sin 与 cos):
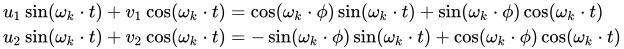
3)解出矩阵
$$M$$
:
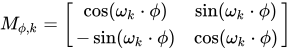
4)它看起来非常像线性代数里的旋转矩阵,这也为后面的 RoPE 做了铺垫。
这件事为什么重要?
- 更容易表示相对距离:注意力可以更轻松地关注 token 间的相对偏移。
- 更容易学位置相关模式:例如“not”常修饰附近词,它更依赖相对邻近关系,而不是绝对位置。
为什么 Sinusoidal Encoding 有效?
结合上面的直觉与性质,可以总结为:
- Uniqueness(可区分性):每个位置都有一组高低频混合的独特模式,模型能区分不同位置。
- Relative position friendly(相对位置友好):固定 offset 可以用线性关系表达,利于学习相对位置模式。
- Bounded range(数值稳定):sin/cos 输出范围稳定在 [-1, 1],长序列下不易数值爆炸。
编码后 embedding 的差分可视化(Absolute PE)
为了更直观地看“位置信息到底注入到了哪里”,我们做一个小实验:
- 生成一个 128 维 dummy embedding(代表一个 token)。
- 分别在 position 0、50、99 处加上位置编码。
- 计算差分,分离出“位置变化带来的影响”。
代码如下(保持不改动):
np.random.seed(42)
dummy_embedding = np.random.randn(d_model)
positions = [0, 50, 99]
encoded_embeddings = [dummy_embedding + pe[pos] for pos in positions]
fig, axs = plt.subplots(2, 1, figsize=(12, 10))
fig.suptitle('Difference in Encoded Embeddings (Absolute Position Encoding)', fontsize=16)
diff_50 = encoded_embeddings[1] - encoded_embeddings[0]
axs[0].plot(diff_50)
axs[0].set_title('Absolute PE: Encoded Embedding (Position 50) - Encoded Embedding (Position 0)')
axs[0].set_xlabel('Dimension')
axs[0].set_ylabel('Difference')
axs[0].grid(True, linestyle='--', alpha=0.7)
diff_99 = encoded_embeddings[2] - encoded_embeddings[0]
axs[1].plot(diff_99)
axs[1].set_title('Absolute PE: Encoded Embedding (Position 99) - Encoded Embedding (Position 0)')
axs[1].set_xlabel('Dimension')
axs[1].set_ylabel('Difference')
axs[1].grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
结果图:
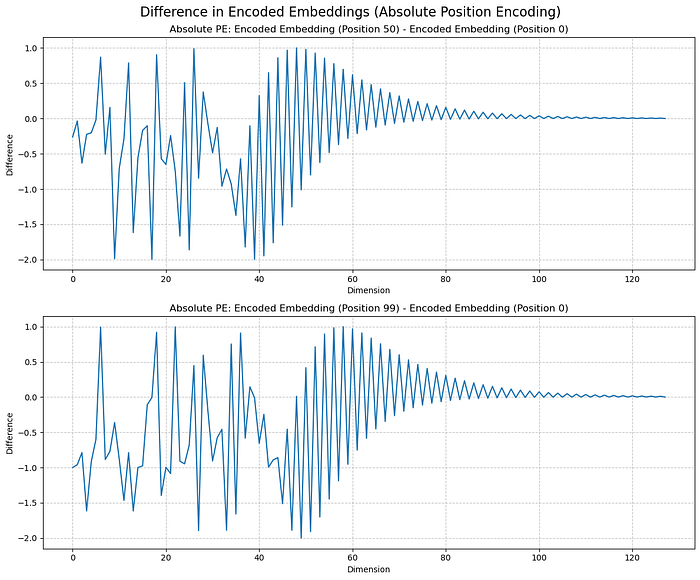
关键观察(原意保留,表述优化):
- 位置信息更集中在前几个维度:前段维度差异最大,说明位置影响更强。
- 随维度增大,幅度衰减:越往后的位置差异越小,后段维度受影响更弱。
- token 语义保存更好:后段维度变化小,意味着更偏向保留 token 本身信息。
- 差分呈周期性:符合 sin/cos 的周期特征。
可能的含义:
- embedding 维度可能存在“分工”:前段偏位置、后段偏语义。
- 注意力或许会更容易从前段维度中抽取位置关系。
- 这在一定程度上平衡了“语义 + 位置”的信息注入方式。
Rotary Position Embedding(RoPE)
Sinusoidal PE 很成功,但后续研究仍在探索更贴合注意力机制的编码方式。RoPE(Su et al.)在论文 RoFormer: Enhanced Transformer with Rotary Position Embedding 中提出,并被许多新模型采用。
RoPE 的基本想法
RoPE 与“加法型”位置编码不同,它做的是“旋转”:
- 不再把一个独立 PE 向量加到 embedding 上。
- 而是对 token embedding(更准确说是 Q/K)做旋转变换。
- 旋转角度由位置 m 与维度共同决定。
- 旋转会保持向量范数(norm)不变,同时把位置信息编码进角度中。
RoPE 的直觉:从 self-attention 的点积看起
理解 RoPE,最好从自注意力开始。
1)序列表示
- 序列 token:
$$w_1, w_2, \ldots, w_L$$
- 每个 token 映射到
$$|D|$$
维 embedding:$$x_1, x_2, \ldots, x_L$$
图示:
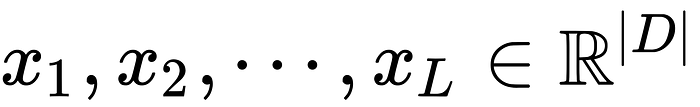
2)注意力的基本计算
在 Transformer 中,每个位置 m 会生成 query
$$q_m$$
和 key
$$k_m$$
,一般由两个映射函数
$$f_q, f_k$$
得到(图示如下):
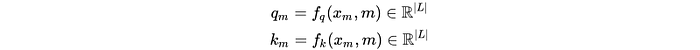
注意力要同时体现两类信息:
- Token Similarity:语义相近的 token,注意力分数应更高(如 cat/dog)。
- Positional Proximity:序列上距离更近的词,往往更相关。
注意力打分通常就是点积(图示):
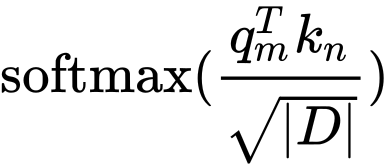
点积可以写成:
$$q \cdot k = ||q||\,||k||\cos(\theta)$$
- Magnitude(模长项):更多体现 token 语义相似性(embedding 相似)。
- Angle(夹角项):可以承载位置相关性(尤其当我们把“位置”编码进角度)。
这给了 RoPE 一个非常自然的切入点:
- 保持模长不变(不破坏语义相似性)
- 通过旋转改变角度(注入位置信息)
RoPE 的目标:让注意力更依赖相对距离
RoPE 的核心诉求可以口语化理解为:
让注意力分数更多取决于“相距多远”,而不是“各自处在第几个位置”。
数学上,文中用图表达为:
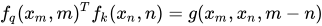
也就是:注意力在 positions m 与 n 之间的关系应主要由内容
$$x_m, x_n$$
和相对位移
$$m-n$$
决定。
这就像你更关心 “not” 是否紧挨着 “happy”,而不是它们是不是句子的第 5、6 个词。
同时,RoPE 也在“绝对位置”与“相对位置”之间做了折中:
- 每个 token 通过旋转仍保留一定绝对位置信息。
- 在点积交互时,相对角度更容易反映相对距离。
- 模型因此更容易同时利用绝对与相对结构。
推导过程原文选择跳过(避免文章过长);可参考 ROFORMER 论文,或以下解释链接(纯 URL 前后加空格以便阅读):
https://pub.towardsai.net/an-in-depth-exploration-of-rotary-position-embedding-rope-ac351a45c794
数学形式:2D 情况(原图保留)
对于 query vector:
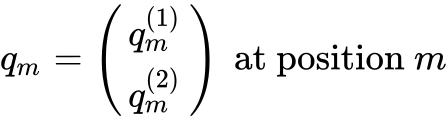
旋转矩阵
$$R_{\theta,m}$$
是一个 2×2 矩阵(原图):
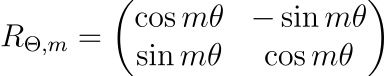
其中
$$\theta \in \mathbb{R}$$
为预设的非零常数。我们用该矩阵旋转向量
$$q$$
,得到旋转后的
$$\hat{q}$$
。
可视化如下(黑色为原向量,不同 m 对应不同旋转后的向量):
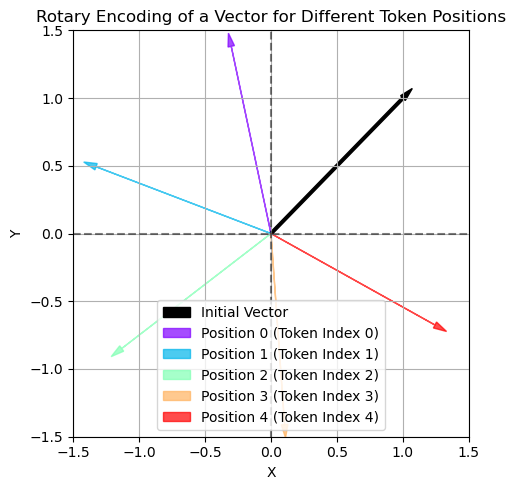
2D embedding represented at different positions
更一般的形式(d 维,原图保留)
一般情况下,将 d 维空间拆成
$$d/2$$
个二维子空间,对每个子空间分别做旋转。
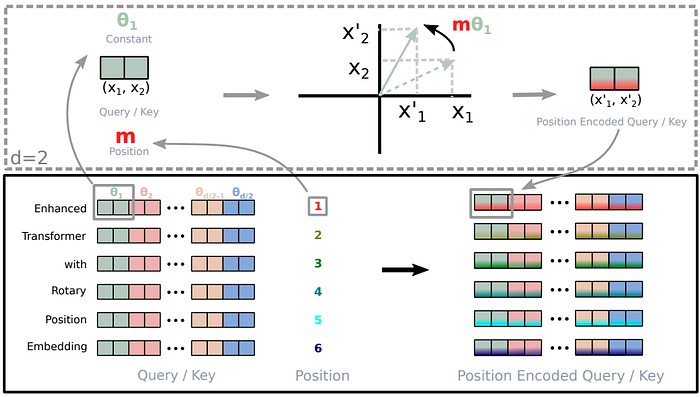
拆分示意(“Enhanced” 的 embedding 被分成
$$d/2$$
个子空间):

The embedding vector for “Enhanced” is divided into d/2 subspaces
每个子空间使用旋转矩阵(原图):
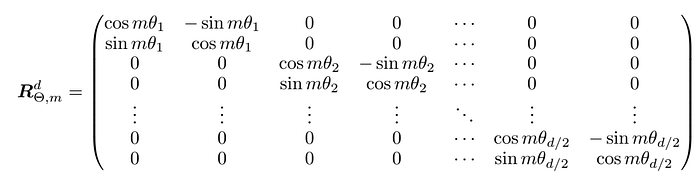
其中参数(原图):
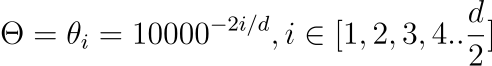
关键观察:
$$\theta$$
会随子空间索引增大而衰减。- 前面的子空间(较小索引)旋转更明显;越到后面,旋转几乎可以忽略。
Python:RoPE 旋转矩阵(代码保持不改动)
下面是 RoPE 的 Python 实现:构造一个 3D 矩阵,每个 slice 对应位置 m 的旋转矩阵。也就是:第一个 Q/K 乘第一个 slice,第二个乘第二个……以此类推。
import numpy as np
import matplotlib.pyplot as plt
def get_rotary_matrix(context_len: int, d_model: int) -> np.ndarray:
"""
Generate the Rotary Matrix for ROPE
Args:
context_len (int): context len
d_model (int): embedding dim
Returns:
np.ndarray: the rotary matrix of dimension context_len x d_model x d_model
"""
R = np.zeros((context_len, d_model, d_model))
positions = np.arange(1, context_len + 1)[:, np.newaxis]
# Create matrix theta (shape: context_len x d_model // 2)
slice_i = np.arange(0, d_model // 2)
theta = 10000. ** (-2.0 * slice_i.astype(float) / d_model)
m_theta = positions * theta
# Create sin and cos values
cos_values = np.cos(m_theta)
sin_values = np.sin(m_theta)
# Populate the rotary matrix R using advanced indexing
R[:, 2*slice_i, 2*slice_i] = cos_values
R[:, 2*slice_i, 2*slice_i+1] = -sin_values
R[:, 2*slice_i+1, 2*slice_i] = sin_values
R[:, 2*slice_i+1, 2*slice_i+1] = cos_values
return R
Efficient Implementation(原图保留)
由于旋转矩阵非常稀疏,论文也给出了更高效的计算方式(原图):
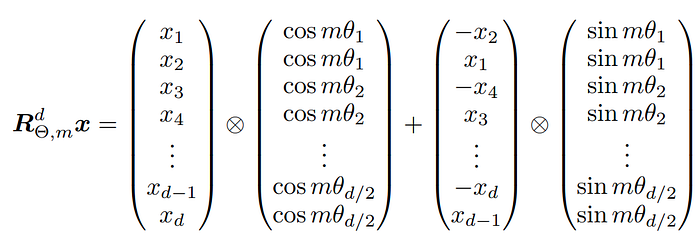
你可以把它当成一个练习:在不显式构造
$$d \times d$$
矩阵的情况下,直接对向量做旋转。
可视化 RoPE:不同位置的旋转效果
下面的代码生成 dummy embedding,并比较 position 0、50、99 的旋转后向量。
context_len = 100
d_model = 128
R = get_rotary_matrix(context_len, d_model)
np.random.seed(42)
# Generate dummy embedding
dummy_embedding = np.random.randn(d_model)
# Positions to encode
positions = [0, 50, 99]
# Create encoded embeddings
encoded_embeddings = [R[pos] @ dummy_embedding for pos in positions]
# Create subplots
fig, axs = plt.subplots(3, 1, figsize=(7, 10))
fig.suptitle('Comparison of Dummy Embedding and Encoded Embeddings', fontsize=16)
# Plot dummy embedding and encoded embedding at position 0
axs[0].plot(dummy_embedding, label='Dummy Embedding')
axs[0].plot(encoded_embeddings[0], label='Encoded Embedding (Position 0)')
axs[0].set_title('Dummy Embedding vs Encoded Embedding (Position 0)')
axs[0].set_xlabel('Dimension')
axs[0].set_ylabel('Value')
axs[0].legend()
axs[0].grid(True, linestyle='--', alpha=0.7)
# Plot dummy embedding and encoded embedding at position 50
axs[1].plot(dummy_embedding, label='Dummy Embedding')
axs[1].plot(encoded_embeddings[1], label='Encoded Embedding (Position 50)')
axs[1].set_title('Dummy Embedding vs Encoded Embedding (Position 50)')
axs[1].set_xlabel('Dimension')
axs[1].set_ylabel('Value')
axs[1].legend()
axs[1].grid(True, linestyle='--', alpha=0.7)
# Plot dummy embedding and encoded embedding at position 99
axs[2].plot(dummy_embedding, label='Dummy Embedding')
axs[2].plot(encoded_embeddings[2], label='Encoded Embedding (Position 99)')
axs[2].set_title('Dummy Embedding vs Encoded Embedding (Position 99)')
axs[2].set_xlabel('Dimension')
axs[2].set_ylabel('Value')
axs[2].legend()
axs[2].grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
效果图:
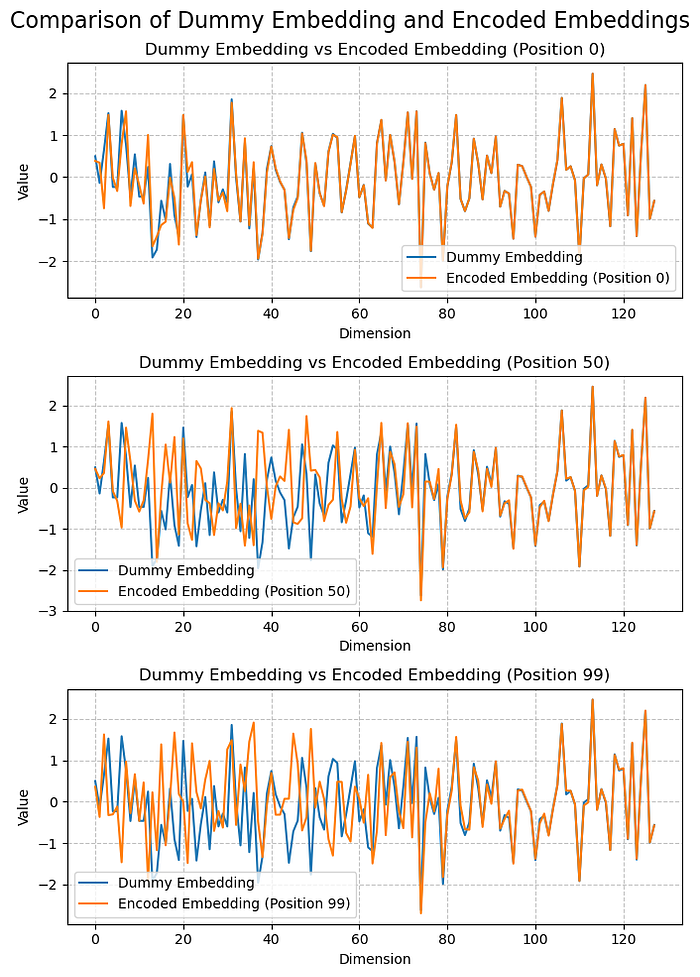
观察橙色线(旋转后的向量)在 position 0、50、99 的变化,你会再次看到:
- 前几个子空间旋转幅度明显更大
- 后面子空间旋转越来越弱
把它和 Absolute PE 的差分观察对照,会发现很多结论一致。
关键观察:
- 位置信息更集中在前几个维度(TRUE HERE ALSO)
- 随维度增大,幅度衰减(TRUE HERE ALSO)
- token 语义保存更好(TRUE HERE ALSO)
Implications:
- 维度分工依旧存在:前段偏位置,后段偏语义。
- 注意力可能更容易利用这些结构化差异。
- 这种设计在“注入位置”与“保留语义”之间维持了平衡。
实践对比:Sinusoidal vs RoPE
从 RoFormer 论文给出的结果来看(原图保留):

The RoFormer gives better BLEU scores compared to its baseline alternative Vaswani et al. [2017] on the WMT 2014 English-to-German translation task
以及训练过程曲线(原图):
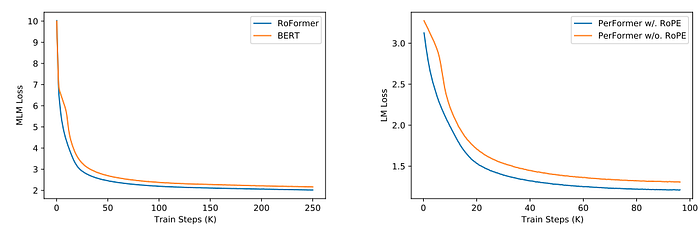
Rotary positional encoding 看起来拥有更好的收敛速度。
并且,很多近期模型(例如 Gemma 2、LLama 3 等)都使用了 RoPE 编码。
References(纯 URL 前后加空格)
BibTeX:
@article{paleti2024:positionalencoding,
title = "Positional Encoding Explained: A Deep Dive into Transformer PE",
author = "Paleti, Nikhil Chowdary",
journal = "Medium",
year = "2024"
}
延伸阅读
如果你想继续系统整理 Transformer、位置编码、注意力机制与工程实现细节,可以到 云栈社区 查找相关主题与讨论。
另外,本文的代码示例基于 Python 生态(NumPy/Matplotlib),便于你快速复现图表与实验。