在强化学习中,标准的深度Q网络(DQN)使用 max Q(s',a') 来计算目标值。这相当于在挑选Q值最高的动作,但这些候选中包含了那些因为估计噪声而被高估的动作,因此会导致过估计偏差。其直接后果是训练不稳定、策略次优。
本文将深入剖析这个问题,内容包括:DQN为何会产生过估计、Double DQN如何解耦动作选择与评估、Dueling DQN如何分离状态值与动作优势、优先经验回放如何实现更智能的采样,并附上使用PyTorch从头实现这些改进的完整代码。最后,还会介绍一个来自CleanRL的专业实现。
过估计问题
DQN的目标值计算公式如下:
y = r + γ·maxₐ' Q(s', a'; θ⁻)
问题的根源在于,同一个网络既负责选择动作(a* = argmax Q),又负责评估这个动作的价值。Q值本身是带有噪声的估计,因此有时噪声会使较差动作的Q值偏高,而取最大值的操作天生偏向于选择那些被高估的动作。
从数学上可以给出一个直观的解释:
E[max(X₁, X₂, ..., Xₙ)] ≥ max(E[X₁], E[X₂], ..., E[Xₙ])
最大值的期望总是大于或等于期望的最大值,这是由凸函数的Jensen不等式决定的。
过估计会带来一系列负面影响:首先,它导致收敛速度变慢,智能体将时间浪费在探索那些被高估的动作上;其次,策略质量会打折扣,高噪声的动作可能比真正好的动作更受青睐;更糟糕的是,过估计会不断累积,甚至导致训练发散;最后,泛化能力也会受损——在状态空间的噪声区域,智能体会表现得过于自信。
Double DQN:解耦选择与评估
标准的DQN让一个网络承担两项任务:
a* = argmaxₐ' Q(s', a'; θ⁻) # 选择最佳动作
y = r + γ · Q(s', a*; θ⁻) # 评估这个动作(使用同一网络)
而Double DQN使用两个网络,各司其职:
a* = argmaxₐ' Q(s', a'; θ) # 用当前在线网络选择动作
y = r + γ · Q(s', a*; θ⁻) # 用目标网络评估该动作的价值
当前在线网络(参数θ)负责选择动作,目标网络(参数θ⁻)负责评估。两个网络的估计误差不相关,从而打破了最大化偏差。
为什么这种方法有效呢?假设当前网络错误地高估了动作a的价值,参数不同的目标网络大概率不会犯同样的错误。由于误差相互独立,它们倾向于相互抵消,而不是累加。
一个通俗的比喻是:DQN像是自己给菜品打分、然后自己挑菜吃,这样烂菜就可能混进来;而Double DQN让朋友打分、你自己来挑,两边的误差就对冲掉了。
Standard DQN: E[Q(s, argmaxₐ Q(s,a))] ≥ maxₐ E[Q(s,a)] (有偏)
Double DQN: E[Q₂(s, argmaxₐ Q₁(s,a))] ≈ maxₐ E[Q(s,a)] (近似无偏)
从DQN升级到Double DQN,核心改动通常只有一行代码:
# DQN 目标计算
next_q_values = target_network(next_states).max(1)[0]
target = rewards + gamma * next_q_values * (1 - dones)
# Double DQN 目标计算
next_actions = current_network(next_states).argmax(1) # <- 用当前网络选择动作
next_q_values = target_network(next_states).gather(1, next_actions.unsqueeze(1)) # <- 用目标网络评估
target = rewards + gamma * next_q_values.squeeze() * (1 - dones)
就是这一行改动,效果却非常显著。
实现:Double DQN
以下是扩展自基础DQN的Double DQN智能体实现:
class DoubleDQNAgent(DQNAgent):
"""
Double DQN: 通过解耦动作选择和评估来减少过估计偏差。
"""
def __init__(self, *args, **kwargs):
"""
初始化 Double DQN agent。
从 DQN 继承所有内容,只改变目标计算。
"""
super().__init__(*args, **kwargs)
def update(self) -> Dict[str, float]:
"""
执行 Double DQN 更新。
Returns:
metrics: 训练指标
"""
if len(self.replay_buffer) < self.batch_size:
return {}
# 采样批次
states, actions, rewards, next_states, dones = self.replay_buffer.sample(
self.batch_size
)
states = states.to(self.device)
actions = actions.to(self.device)
rewards = rewards.to(self.device)
next_states = next_states.to(self.device)
dones = dones.to(self.device)
# 当前 Q 值 Q(s,a;θ)
current_q_values = self.q_network(states).gather(1, actions.unsqueeze(1))
# Double DQN 目标计算
with torch.no_grad():
# 使用当前网络选择动作
next_actions = self.q_network(next_states).argmax(1)
# 使用目标网络评估动作
next_q_values = self.target_network(next_states).gather(
1, next_actions.unsqueeze(1)
).squeeze()
# 计算目标
target_q_values = rewards + (1 - dones) * self.gamma * next_q_values
# 计算损失
loss = F.mse_loss(current_q_values.squeeze(), target_q_values)
# 梯度下降
self.optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(self.q_network.parameters(), max_norm=10.0)
self.optimizer.step()
self.training_step += 1
return {
'loss': loss.item(),
'q_mean': current_q_values.mean().item(),
'q_std': current_q_values.std().item(),
'target_q_mean': target_q_values.mean().item()
}
配套的训练函数:
def train_double_dqn(
env_name: str,
n_episodes: int = 1000,
max_steps: int = 500,
train_freq: int = 1,
eval_frequency: int = 50,
eval_episodes: int = 10,
verbose: bool = True,
**kwargs
) -> Tuple:
"""
训练 Double DQN agent(使用 DoubleDQNAgent 而不是 DQNAgent)。
"""
# 与 train_dqn 相同但使用 DoubleDQNAgent
env = gym.make(env_name)
eval_env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
# 使用 DoubleDQNAgent
agent = DoubleDQNAgent(
state_dim=state_dim,
action_dim=action_dim,
**kwargs
)
# 训练循环(与 DQN 相同)
stats = {
'episode_rewards': [],
'episode_lengths': [],
'losses': [],
'q_values': [],
'target_q_values': [],
'eval_rewards': [],
'eval_episodes': [],
'epsilons': []
}
print(f"Training Double DQN on {env_name}")
print(f"State dim: {state_dim}, Action dim: {action_dim}")
print("="*70)
for episode in range(n_episodes):
state, _ = env.reset()
episode_reward = 0
episode_length = 0
episode_metrics = []
for step in range(max_steps):
action = agent.select_action(state, training=True)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
agent.store_transition(state, action, reward, next_state, done)
if step % train_freq == 0:
metrics = agent.update()
if metrics:
episode_metrics.append(metrics)
episode_reward += reward
episode_length += 1
state = next_state
if done:
break
# 更新目标网络
if (episode + 1) % kwargs.get('target_update_freq', 10) == 0:
agent.update_target_network()
agent.decay_epsilon()
# 存储统计信息
stats['episode_rewards'].append(episode_reward)
stats['episode_lengths'].append(episode_length)
stats['epsilons'].append(agent.epsilon)
if episode_metrics:
stats['losses'].append(np.mean([m['loss'] for m in episode_metrics]))
stats['q_values'].append(np.mean([m['q_mean'] for m in episode_metrics]))
stats['target_q_values'].append(np.mean([m['target_q_mean'] for m in episode_metrics]))
# 评估
if (episode + 1) % eval_frequency == 0:
eval_reward = evaluate_dqn(eval_env, agent, eval_episodes)
stats['eval_rewards'].append(eval_reward)
stats['eval_episodes'].append(episode + 1)
if verbose:
avg_reward = np.mean(stats['episode_rewards'][-50:])
avg_loss = np.mean(stats['losses'][-50:]) if stats['losses'] else 0
avg_q = np.mean(stats['q_values'][-50:]) if stats['q_values'] else 0
print(f"Episode {episode+1:4d} | "
f"Reward: {avg_reward:7.2f} | "
f"Eval: {eval_reward:7.2f} | "
f"Loss: {avg_loss:7.4f} | "
f"Q: {avg_q:6.2f} | "
f"ε: {agent.epsilon:.3f}")
env.close()
eval_env.close()
print("="*70)
print("Training complete!")
return agent, stats
以LunarLander-v3环境为例进行训练:
# 训练 Double DQN
if __name__ == "__main__":
device = 'cuda' if torch.cuda.is_available() else 'cpu'
agent_ddqn, stats_ddqn = train_double_dqn(
env_name='LunarLander-v3',
n_episodes=4000,
max_steps=1000,
learning_rate=5e-4,
gamma=0.99,
epsilon_start=1.0,
epsilon_end=0.01,
epsilon_decay=0.9995,
buffer_capacity=100000,
batch_size=128,
target_update_freq=20,
train_freq=4,
eval_frequency=100,
eval_episodes=10,
hidden_dims=[256, 256],
device=device,
verbose=True
)
# 保存模型
agent_ddqn.save('doubledqn_lunar_lander.pth')
训练输出示例:
Training Double DQN on LunarLander-v3
State dim: 8, Action dim: 4
======================================================================
Episode 100 | Reward: -155.24 | Eval: -885.72 | Loss: 52.9057 | Q: 0.20 | ε: 0.951
Episode 200 | Reward: -148.85 | Eval: -85.94 | Loss: 37.2449 | Q: 2.14 | ε: 0.905
...
Episode 3900 | Reward: 177.70 | Eval: 259.99 | Loss: 36.2971 | Q: 40.22 | ε: 0.142
Episode 4000 | Reward: 156.60 | Eval: 251.17 | Loss: 46.7266 | Q: 42.15 | ε: 0.135
======================================================================
Training complete!
Dueling DQN:分离状态价值与动作优势
在许多状态下,选择哪个具体动作其实差别不大。例如,在CartPole中杆子刚好平衡时,向左或向右微调都可以;在赛车游戏中直线行驶时,方向盘的微小调整结果也差不多;在LunarLander中,距离地面还很远时,引擎怎么喷射影响也有限。
标准DQN为每个动作单独学习Q(s,a),这可能会将网络容量浪费在冗余信息上。Dueling DQN的核心思路是将Q值分解为两部分:V(s)表示“这个状态本身值多少”,A(s,a)表示“执行这个动作比平均动作水平好多少”。
网络架构对比如下:
标准 DQN:
Input -> Hidden Layers -> Q(s,a₁), Q(s,a₂), ..., Q(s,aₙ)
Dueling DQN:
|-> Value Stream -> V(s)
Input -> Shared Layers |
|-> Advantage Stream -> A(s,a₁), A(s,a₂), ..., A(s,aₙ)
Q(s,a) = V(s) + (A(s,a) - mean(A(s,·)))
为什么要减去优势的均值?如果不这样做,任何常数加到V(s)上同时从A(s,a)中减去,得到的Q(s,a)完全不变,网络将无法学习到唯一的解。
数学表达式如下:
Q(s,a) = V(s) + A(s,a) - (1/|A|)·Σₐ' A(s,a')
实践中,有时使用最大值代替均值效果更好:
Q(s,a) = V(s) + A(s,a) - maxₐ' A(s,a')
举例说明:假设V(s) = 10,好动作的优势A是+5,差动作的优势A是-3,平均优势 = (+5-3)/2 = +1。那么:
- Q(s, 好动作) = 10 + 5 - 1 = 14
- Q(s, 差动作) = 10 - 3 - 1 = 6
Dueling架构的实现如下:
class DuelingQNetwork(nn.Module):
"""
Dueling DQN 架构,分离状态价值和动作优势。
理论: Q(s,a) = V(s) + A(s,a) - mean(A(s,·))
"""
def __init__(
self,
state_dim: int,
action_dim: int,
hidden_dims: List[int] = [128, 128]
):
"""
初始化 Dueling Q 网络。
Args:
state_dim: 状态空间维度
action_dim: 动作数量
hidden_dims: 共享层大小
"""
super(DuelingQNetwork, self).__init__()
self.state_dim = state_dim
self.action_dim = action_dim
# 共享特征提取器
shared_layers = []
input_dim = state_dim
for hidden_dim in hidden_dims:
shared_layers.append(nn.Linear(input_dim, hidden_dim))
shared_layers.append(nn.ReLU())
input_dim = hidden_dim
self.shared_network = nn.Sequential(*shared_layers)
# 值流: V(s) = 状态的标量值
self.value_stream = nn.Sequential(
nn.Linear(hidden_dims[-1], 128),
nn.ReLU(),
nn.Linear(128, 1)
)
# 优势流: A(s,a) = 每个动作的优势
self.advantage_stream = nn.Sequential(
nn.Linear(hidden_dims[-1], 128),
nn.ReLU(),
nn.Linear(128, action_dim)
)
# 初始化权重
self.apply(self._init_weights)
def _init_weights(self, module):
"""初始化网络权重。"""
if isinstance(module, nn.Linear):
nn.init.kaiming_normal_(module.weight, nonlinearity='relu')
nn.init.constant_(module.bias, 0.0)
def forward(self, state: torch.Tensor) -> torch.Tensor:
"""
通过 dueling 架构的前向传播。
Args:
state: 状态批次, 形状 (batch_size, state_dim)
Returns:
q_values: 所有动作的 Q(s,a), 形状 (batch_size, action_dim)
"""
# 共享特征
features = self.shared_network(state)
# 值: V(s) -> 形状 (batch_size, 1)
value = self.value_stream(features)
# 优势: A(s,a) -> 形状 (batch_size, action_dim)
advantages = self.advantage_stream(features)
# 组合: Q(s,a) = V(s) + A(s,a) - mean(A(s,·))
q_values = value + advantages - advantages.mean(dim=1, keepdim=True)
return q_values
Dueling架构的优势在于:在动作影响不大的状态下能学得更好,梯度流动更通畅因而收敛更快,价值估计也更加稳健。
我们还可以将两种改进结合起来,构建Double Dueling DQN:
class DoubleDuelingDQNAgent(DoubleDQNAgent):
"""
结合 Double DQN 和 Dueling DQN 的智能体。
"""
def __init__(
self,
state_dim: int,
action_dim: int,
hidden_dims: List[int] = [128, 128],
**kwargs
):
"""
初始化 Double Dueling DQN 智能体。
使用 DuelingQNetwork 而不是标准 QNetwork。
"""
# 我们需要以不同方式设置网络
self.state_dim = state_dim
self.action_dim = action_dim
self.gamma = kwargs.get('gamma', 0.99)
self.batch_size = kwargs.get('batch_size', 64)
self.target_update_freq = kwargs.get('target_update_freq', 10)
self.device = torch.device(kwargs.get('device', 'cpu'))
# 探索参数
self.epsilon = kwargs.get('epsilon_start', 1.0)
self.epsilon_end = kwargs.get('epsilon_end', 0.01)
self.epsilon_decay = kwargs.get('epsilon_decay', 0.995)
# 使用 Dueling 架构
self.q_network = DuelingQNetwork(
state_dim, action_dim, hidden_dims
).to(self.device)
self.target_network = DuelingQNetwork(
state_dim, action_dim, hidden_dims
).to(self.device)
self.target_network.load_state_dict(self.q_network.state_dict())
self.target_network.eval()
# 优化器
learning_rate = kwargs.get('learning_rate', 1e-3)
self.optimizer = torch.optim.Adam(self.q_network.parameters(), lr=learning_rate)
# 回放缓冲区
buffer_capacity = kwargs.get('buffer_capacity', 100000)
self.replay_buffer = ReplayBuffer(buffer_capacity)
# 统计
self.episode_count = 0
self.training_step = 0
# update() 方法继承自 DoubleDQNAgent
优先经验回放
并非所有的经验转换都具有同等的学习价值。时序差分误差(TD Error)大的转换说明当前预测严重偏离现实,从中能学到更多东西;而TD误差小的转换说明网络已经学得差不多了,再次采样意义不大。
均匀采样将所有转换一视同仁,这浪费了关键的学习机会。优先经验回放的核心思路是:让更重要的转换(即TD误差大的转换)有更高的概率被采样到。
优先级计算公式如下:
pᵢ = |δᵢ| + ε
其中:
δᵢ = r + γ·max Q(s',a') - Q(s,a) (TD 误差)
ε = 一个小常数,保证所有转换都有被采样的可能
采样概率基于优先级:
P(i) = pᵢ^α / Σⱼ pⱼ^α
α 控制优先化程度:
α = 0 -> 退化成均匀采样
α = 1 -> 完全按优先级比例采样
优先采样改变了数据的原始分布,会引入偏差。解决办法是使用重要性采样权重来修正更新:
wᵢ = (N · P(i))^(-β)
β 控制校正力度:
β = 0 -> 不校正
β = 1 -> 完全校正
通常β从0.4左右开始,随着训练过程逐渐增大到1.0。
以下是一个简化的优先经验回放缓冲区实现(生产环境通常会使用SumTree数据结构以获得O(log N)的采样复杂度):
class PrioritizedReplayBuffer:
"""
优先经验回放缓冲区。
理论: 按 TD 误差比例采样转换。我们可以从中学到更多的转换会被更频繁地采样。
"""
def __init__(self, capacity: int, alpha: float = 0.6, beta: float = 0.4):
"""
Args:
capacity: 缓冲区最大容量
alpha: 优先化指数(0=均匀, 1=比例)
beta: 重要性采样指数(退火到 1.0)
"""
self.capacity = capacity
self.alpha = alpha
self.beta = beta
self.beta_increment = 0.001 # 随时间退火 beta
self.buffer = []
self.priorities = np.zeros(capacity, dtype=np.float32)
self.position = 0
def push(self, state, action, reward, next_state, done):
"""
以最大优先级添加转换。
理论: 新转换获得最大优先级(会很快被采样)。它们的实际优先级在首次 TD 误差计算后更新。
"""
max_priority = self.priorities.max() if self.buffer else 1.0
if len(self.buffer) < self.capacity:
self.buffer.append((state, action, reward, next_state, done))
else:
self.buffer[self.position] = (state, action, reward, next_state, done)
self.priorities[self.position] = max_priority
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size: int):
"""
按优先级比例采样批次。
Returns:
batch: 采样的转换
indices: 采样转换的索引(用于优先级更新)
weights: 重要性采样权重
"""
if len(self.buffer) == self.capacity:
priorities = self.priorities
else:
priorities = self.priorities[:len(self.buffer)]
# 计算采样概率
probs = priorities ** self.alpha
probs /= probs.sum()
# 采样索引
indices = np.random.choice(len(self.buffer), batch_size, p=probs, replace=False)
# 获取转换
batch = [self.buffer[idx] for idx in indices]
# 计算重要性采样权重
total = len(self.buffer)
weights = (total * probs[indices]) ** (-self.beta)
weights /= weights.max() # 归一化以保持稳定性
# 退火 beta
self.beta = min(1.0, self.beta + self.beta_increment)
# 转换为 tensor
states, actions, rewards, next_states, dones = zip(*batch)
states = torch.FloatTensor(np.array(states))
actions = torch.LongTensor(actions)
rewards = torch.FloatTensor(rewards)
next_states = torch.FloatTensor(np.array(next_states))
dones = torch.FloatTensor(dones)
weights = torch.FloatTensor(weights)
return (states, actions, rewards, next_states, dones), indices, weights
def update_priorities(self, indices, td_errors):
"""
根据 TD 误差更新优先级。
Args:
indices: 采样转换的索引
td_errors: 那些转换的 TD 误差
"""
for idx, td_error in zip(indices, td_errors):
self.priorities[idx] = abs(td_error) + 1e-6
def __len__(self):
return len(self.buffer)
DQN变体对比与选型指南
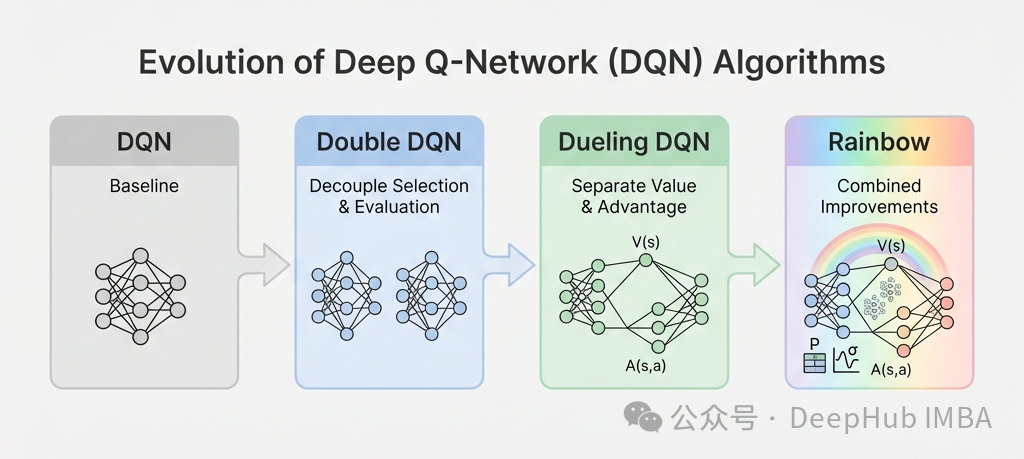
这些DQN变体各自解决了什么问题?
- DQN:作为基线模型,它使用单一网络同时选择动作和评估动作价值。它引入了目标网络来稳定“移动目标”问题,但容易过估计Q值,噪声可能驱使智能体追逐不存在的“幽灵奖励”。
- Double DQN:解耦了动作选择与价值评估。在线网络选择动作,目标网络评估价值。实践表明它能有效抑制不切实际的Q值估计,使学习曲线更加平滑。
- Dueling DQN:改变了网络架构,分别学习状态价值V(s)和动作优势A(s,a)。其核心洞见是:在许多状态下,具体动作的选择影响不大。在像LunarLander这样存在大量“冗余动作”的环境中,样本效率提升显著。
- Double Dueling DQN:结合了上述两者的优点,既减少了估计噪声,又提高了表示效率。在实践中,这个组合通常最为稳健,在达到峰值性能的速度和可靠性上都优于单一改进。

实践建议与排错
如果发现Double DQN的表现比标准DQN还差,可能的原因包括:训练周期不够长(Double DQN起步有时稍慢)、目标网络更新过于频繁、或者学习率设置偏高。可以尝试将训练时间延长、调大target_update_freq参数,或将学习率降低2-5倍。
如果Dueling架构没有带来明显改善,可能是环境本身不适合(所有状态都很关键)、网络容量太小,或者值流/优势流网络深度不够。可以尝试加宽加深网络,并确认环境中确实存在大量“动作中性”的状态。
如果优先经验回放导致训练不稳定,可能是β退火速度太快、α设置过高,或者重要性采样权重没有正确归一化。可以尝试减慢β的增量、将α降至0.4-0.6,并确保权重进行了归一化处理。
选型指南:
- 起步首选Double DQN:代码改动极小,收益明确,几乎没有引入额外复杂度。
- 何时加入Dueling架构:当状态价值比具体动作优势更重要时;环境中存在大量“动作选择影响不大”的状态时;需要更快收敛速度时。
- 何时加入优先经验回放:样本效率至关重要时;有足够的计算预算(PER比均匀采样慢);奖励稀疏,需要帮助智能体关注那些少见的成功经验时。
最后提到的Rainbow算法,集成了六项改进:Double DQN、Dueling DQN、优先经验回放、多步学习(n-step returns)、分布式RL(C51)以及噪声网络(参数空间探索)。其中,多步学习将1步TD回报替换为n步回报:
# 1-step TD:
y = rₜ + γ·max Q(sₜ₊₁, a)
# n-step:
y = rₜ + γ·rₜ₊₁ + γ²·rₜ₊₂ + ... + γⁿ·max Q(sₜ₊ₙ, a)
其好处是信用分配更清晰,能加速学习。
总结
本文从DQN的过估计问题出发,依次介绍了Double DQN、Dueling架构、优先经验回放等改进方案。每种改进都对应一个具体的失败模式:max算子的偏差、低效的状态-动作值表示、以及均匀采样的数据浪费。
通过从头实现这些方法,我们能更深刻地理解它们为何有效。许多“高级”强化学习算法不过是这些简单而强大思想的组合,理解这些基础思想本身,才是构建可扩展智能系统的关键。
欢迎在云栈社区与更多开发者交流强化学习及其他AI技术实践。